线段树模板

单点修改

void update_point(int rt,int x,int k){
    if(tree[rt].l==x&&tree[rt].r==x){
        tree[rt].k=k;
        return ;
    }
    
    int mid=(tree[rt].r+tree[rt].l)>>1;
    
    if(x<=mid){
        update_point(lson,x,k);
    }else{
        update_point(rson,x,k);
    }
    
    push_up(rt);
}

区间修改，区间查询

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define DOF 0x7f7f7f7f
#define endl '
'
#define mem(a,b) memset(a,b,sizeof(a))
#define debug(case,x); cout<<case<<"  : "<<x<<endl;
#define open freopen("ii.txt","r",stdin)
#define close freopen("oo.txt","w",stdout)
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define pb push_back
using namespace std;
#define int long long
#define lson rt<<1
#define rson rt<<1|1
const int maxn=1e6+10;


struct tree{
    int l,r;
    int lazy,sum;
}tree[maxn<<2];

void push_up(int rt){
    tree[rt].sum=tree[lson].sum+tree[rson].sum;

}

void push_down(int rt){
    if(tree[rt].lazy){
        tree[lson].sum=tree[lson].sum+tree[rt].lazy*(tree[lson].r-tree[lson].l+1);
        tree[rson].sum=tree[rson].sum+tree[rt].lazy*(tree[rson].r-tree[lson].l+1);
        tree[lson].lazy+=tree[rt].lazy;
        tree[rson].lazy+=tree[rt].lazy;
        tree[rt].lazy=0;
    }

}


void build(int rt,int l,int r){
    tree[rt].l=l,tree[rt].r=r,tree[rt].lazy=0;
    if(l==r){
        tree[rt].sum=t[l];
        return ;
    }

    int mid=(l+r)>>1;

    build(lson,l,mid);
    build(rson,mid+1,r);
    push_up(rt);

}

void update(int rt,int l,int r,int lazy){
    if(tree[rt].l>=l&&tree[rt].r<=r){
        tree[rt].lazy+=lazy;
        tree[rt].sum=+=(tree[rt].r-tree[rt].l+1)*lazy;
        return ;
    }

    push_down(rt);;

    int mid=(tree[rt].l+tree[rt].r)>>1;

    if(l<=mid){
        update(lson,l,r,lazy);
    }
    if(r>mid){
        update(rson,l,r,lazy);
    }

    push_up(rt);
}

int query(int rt,int l,int r){
    if(tree[rt].l>=l&&tree[rt].r<=r){
        return tree[rt].sum;
    }
    push_down(rt);

    int mid=(tree[rt].l+tree[rt].r)>>1;
    int res=0;

    if(l<=mid){
        res+=query(lson,l,r);
    }
    if(r>mid){
        res+=query(rson,l,r);
    }
    return res;


}

一：线段树介绍

引例a：单点修改[最大值]HDU1754

注意到父亲点和左儿子,右儿子的关系,左儿子的序号是父亲的2倍,右儿子的序号是父亲的2倍+1；

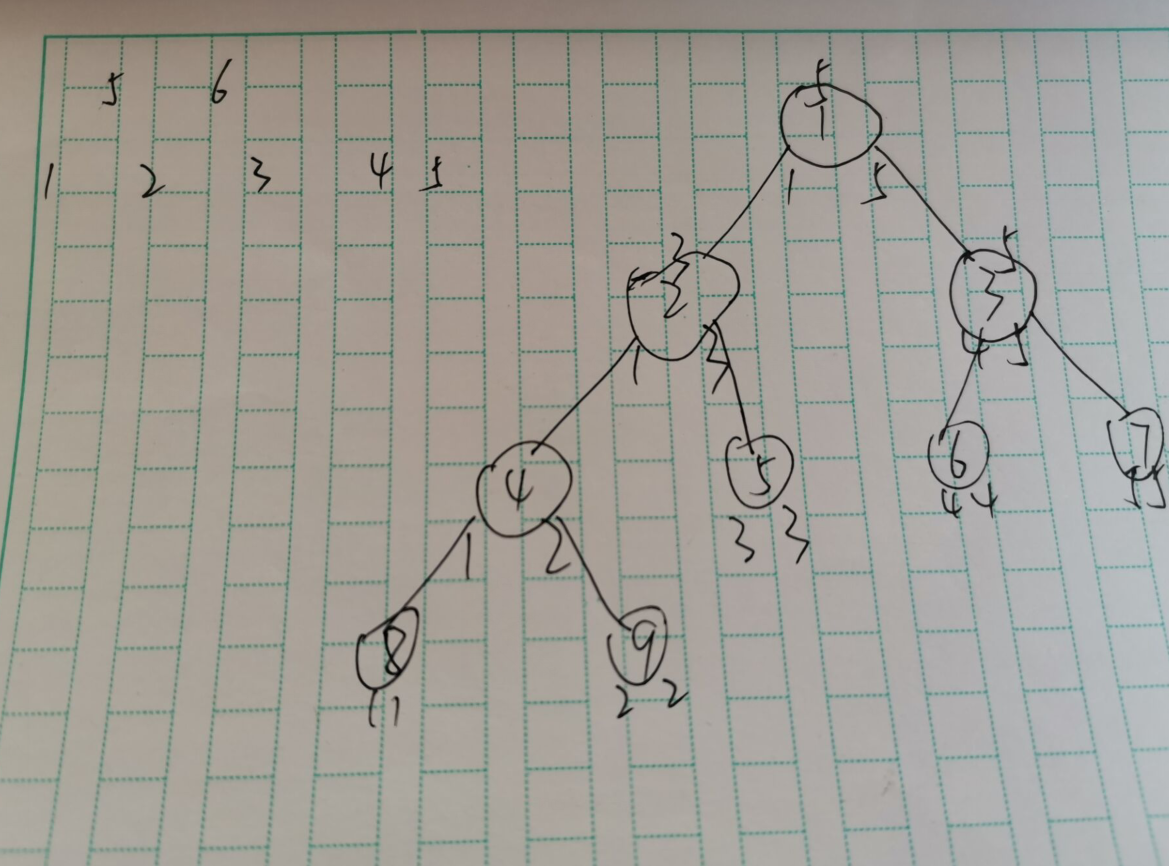
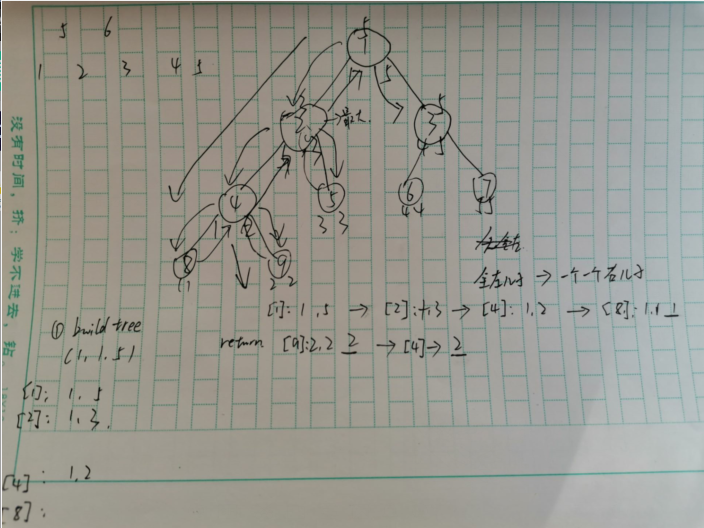
建树的过程如下,先建全部的左儿子然后回溯建右儿子和取区间最大值

#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=2e+5;
int n,m,a[maxn];

struct tree{
    int l,r,v;
}trees[maxn<<2];

1.建树

void buildtree(int s,int l,int r)
{
    trees[s].l=l,trees[s].r=r;
    if(l==r)
    {
        trees[s].v=a[l];
        return ;
    }
    int mid=l+r>>1;

    buildtree(s<<1,l,mid);//左儿子建立
    buildtree(s<<1|1,mid+1,r);//右儿子建立

    trees[s].v=max(trees[s<<1].v,trees[s<<1|1].v);//取区间最大值
}

2.单点修改

void update_point(int s,int a,int m)
{
    if(trees[s].l==a&&trees[s].r==a)
    {
        trees[s].v=m;
        return ;
    }
    int mid=trees[s].l+trees[s].r>>1;

    if(a<=mid)
        update_point(s<<1,a,m);//如果满足这种情况是说明这个点在左儿子的子区间
    if(a>mid)
        update_point(s<<1|1,a,m);//在右儿子的子区间

    trees[s].v=max(trees[s<<1].v,trees[s<<1|1].v);
}

3.区间查询最大值

int ask_interval(int s,int l,int r)
{
    if(trees[s].l==l&&trees[s].r==r)
        return trees[s].v;
    int mid=trees[s].l+trees[s].r>>1;

    if(r<=mid)
        return ask_interval(s<<1,l,r);//全部在左儿子
    if(l>mid)
        return ask_interval(s<<1|1,l,r);//全部在右儿子
    if(l<=mid&&r>mid)
        return max(ask_interval(s<<1,l,mid),ask_interval(s<<1|1,mid+1,r));//左右儿子区间均有

    return 0;
}

引例b：区间修改[“求和”]HDU1698

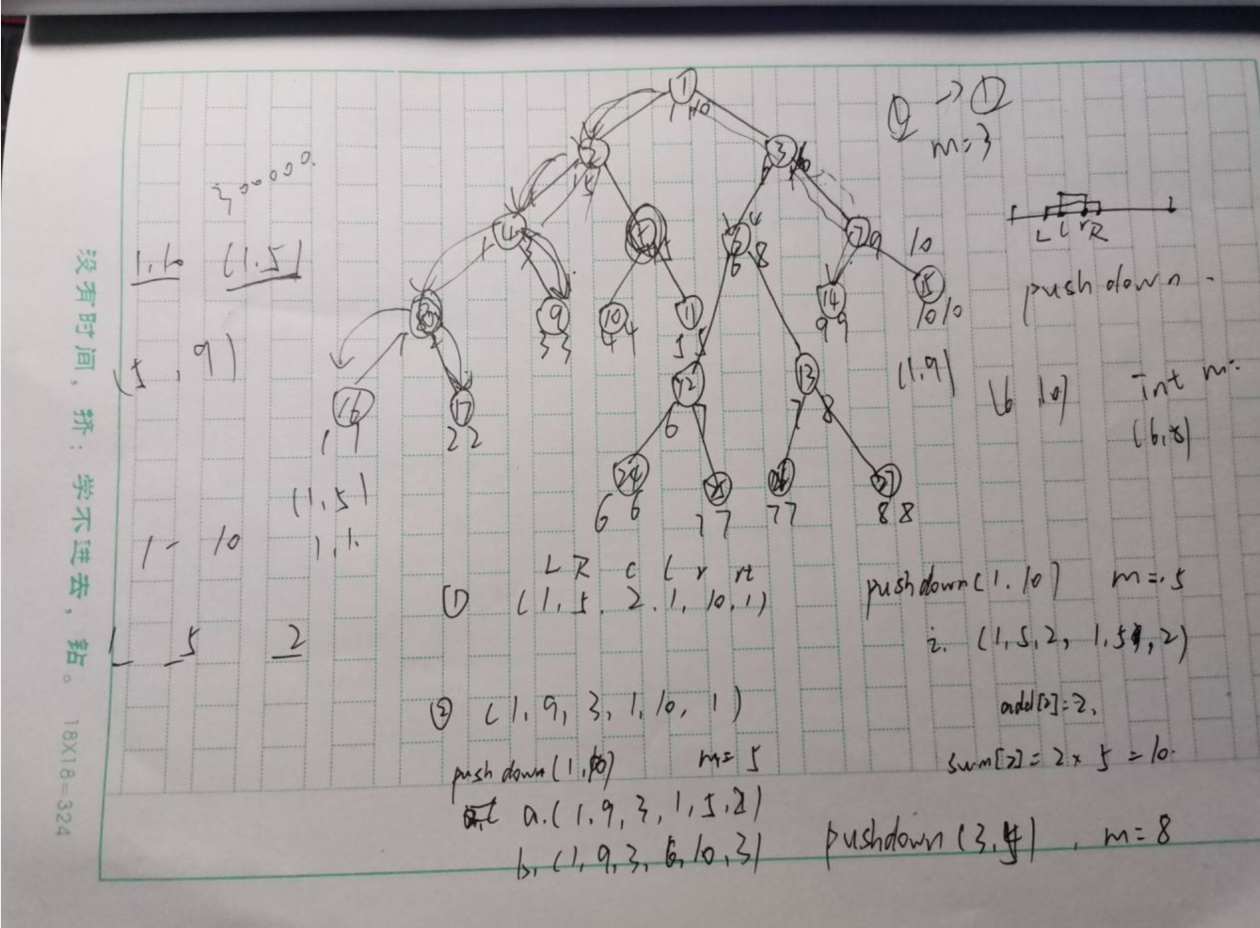
区间操作会Lazy_tag（懒标记）：懒标记的作用方式待补充

此题由于是直接对值的替换所以比较简单，懒标记的作用也不是很明显。

#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=1e5+5;
int n,m;
typedef long long ll;
struct tree{
    int l,r,sum,lazy_tag;
}trees[maxn<<2];

1.建树

void buildtree(int s, int l, int r) {
    trees[s].l = l, trees[s].r = r;
    trees[s].lazy_tag = 0; //注意初始化懒标记，你不初始化，我不初始化，一个代码改一天.
    if(l == r) {
        trees[s].sum = 1;
        return ;
    }
    int m = l + r >> 1;
    buildtree(s << 1, l, m);
    buildtree(s << 1 | 1, m + 1, r);

    trees[s].sum = trees[s << 1].sum + trees[s << 1 | 1].sum;
}

2.懒标记

void pushdown(int s)
{　　 //if(trees[s].lazy_tag)//我的模板在其他函数中直接调用了这句，减少了时间的消耗
    trees[s<<1].lazy_tag=trees[s].lazy_tag;
    trees[s<<1|1].lazy_tag=trees[s].lazy_tag;
    trees[s<<1].sum=trees[s].lazy_tag*(trees[s<<1].r-trees[s<<1].l+1);
    trees[s<<1|1].sum=trees[s].lazy_tag*(trees[s<<1|1].r-trees[s<<1|1].l+1);
    trees[s].lazy_tag=0;

}

3.区间修改（替换为指定值非累加）

void update(int s,int l,int r,int value)
{
    if(l<=trees[s].l&&r>=trees[s].r)
    {
        trees[s].lazy_tag=value;//非累加是替换
        trees[s].sum=value*(trees[s].r-trees[s].l+1);
        return ;

    }

    if(trees[s].lazy_tag) pushdown(s);

    int m=trees[s].l+trees[s].r>>1;

    if(l<=m)
        update(s<<1,l,r,value);
    if(r>m)
        update(s<<1|1,l,r,value);

    trees[s].sum=trees[s<<1].sum+trees[s<<1|1].sum;
}

4.区间查询

int ans;
int query(int s,int l,int r)
{
    if(l<=trees[s].l&&r>=trees[s].r)
        return trees[s].sum;
    if(trees[s].lazy_tag) pushdown(s);
    int ans=0;
    int m=trees[s].r+trees[s].l>>1;

    if(l<=m)
        ans+=query(s<<1,l,r);
    if(r>m)
        ans+=query(s<<1|1,l,r);

    return ans;
}

int ans;
void query(int s,int l,int r)
{

    if(trees[s].l>=l&&trees[s].r<=r)
    {
        ans+=trees[s].sum;
        return ;
    }
    if(trees[s].lazy_tag) pushdown(s);
    int m=trees[s].r+trees[s].l>>1;
    if(l<=m)
        query(s<<1,l,r);
    if(r>m)
        query(s<<1|1,l,r);
}