修了一些我发现的锅,可能还有一些锅,欢迎来锤
其实我也不知道是不是叫这个名字。
假设有一个数组 (a_0,a_1,...,a_{2^n}) ,求一个数组 (b_x=sumlimits_{i|x=x} a_i) ,即子集和。(妈呀不就是 fwt_or 吗)
先上代码:
for(int i=0;i<n;i++)
{
for(int j=0;j<(1<<n);j++)
{
if(j&(1<<i)) a[j]+=a[j^(1<<i)];
}
}
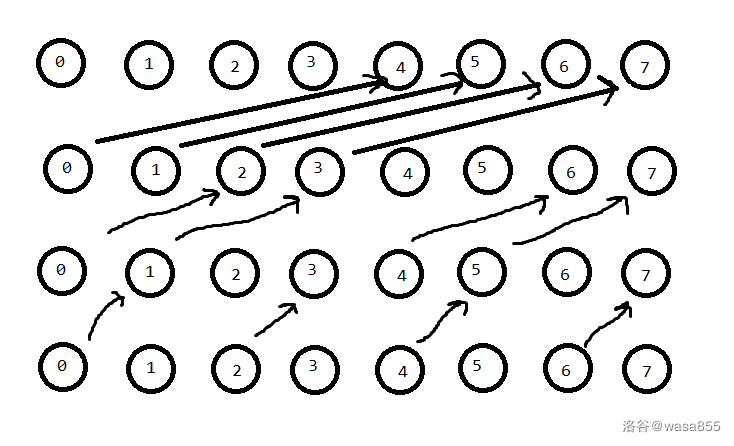
原理:从小到大枚举每一位,然后合并。
如图,显然他是正确的(从下往上看)。
 )
)
假设有一个数组 (a_0,a_1,...,a_{2^n}) ,求一个数组 (b_x=sumlimits_{i&x=x} a_i) ,即超集和。(妈呀不就是 fwt_and 吗)
先上代码:
for(int i=0;i<n;i++)
{
for(int j=0;j<(1<<n);j++)
{
if(!(j&(1<<i))) a[j]+=a[j^(1<<i)];
}
}
原理:从小到大枚举每一位,然后合并。
如果不理解,可以画图手玩。
不是有 fwt 了吗,要这个干什么 。
发现他的性质非常优,不仅可以在 (O(ncdot 2^n)) 的复杂度内维护和,积,(max,min) 等支持交换律操作都可以维护。
题目:CF449D (但是先挖个坑,两天内来填)
我回来填坑了。
对于一个数,假设他出现了 (x) 遍,显然,他被选入答案的方案数是 (2^x-1) 。
算出 (a_i) 为 (i) 的超集和,那么跑一边容斥即可知道答案。