题目描述
给定一棵有n个节点的无根树和m个操作,操作有2类:
1、将节点a到节点b路径上所有点都染成颜色c;
2、询问节点a到节点b路径上的颜色段数量(连续相同颜色被认为是同一段),如“112221”由3段组成:“11”、“222”和“1”。
请你写一个程序依次完成这m个操作。
输入输出格式
输入格式:
第一行包含2个整数n和m,分别表示节点数和操作数;
第二行包含n个正整数表示n个节点的初始颜色
下面 行每行包含两个整数x和y,表示x和y之间有一条无向边。
下面 行每行描述一个操作:
“C a b c”表示这是一个染色操作,把节点a到节点b路径上所有点(包括a和b)都染成颜色c;
“Q a b”表示这是一个询问操作,询问节点a到节点b(包括a和b)路径上的颜色段数量。
输出格式:
对于每个询问操作,输出一行答案。
输入输出样例
输入样例#1:
6 5 2 2 1 2 1 1 1 2 1 3 2 4 2 5 2 6 Q 3 5 C 2 1 1 Q 3 5 C 5 1 2 Q 3 5
输出样例#1:
3 1 2
说明
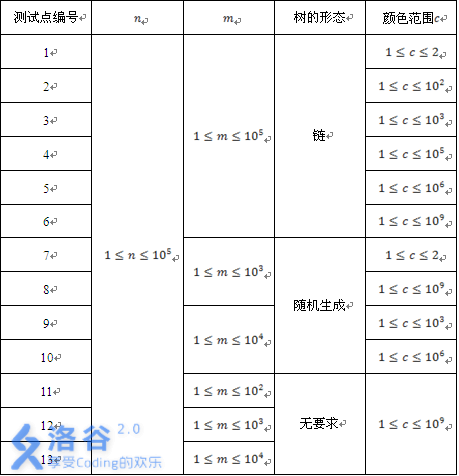

//这个题面一半来自洛谷,一半来自BZOJ
解题思路
树剖套线段树。这题重点在线段树上。线段树的每个节点存下此节点表示的区间范围l、r,这个区间内颜色块数num,l处的颜色lc,r处的颜色rc。
然后从合并两个区间的信息时,特判如果接口处颜色相同,则当前区间num等于两个子区间num之和减一,不相等就不减一(语文不好,勉强看吧)
源代码
#include<vector> #include<cstdio> #include<cstring> #include<algorithm> int n,m; struct Edge{ int next,to; }e[200010]; int head[100010]={0},cnt=1; void add(int u,int v) { e[cnt]={head[u],v}; head[u]=cnt++; } int color[100010]={0}; struct tree{ int fa; int w; int dep; int num_to; int wson; int top; int id; }t[100010]; void dfs1(int fa,int u,int dep) { t[u].fa=fa; t[u].dep=dep; t[u].num_to=1; t[u].wson=-1; int max_to=0,num_son=0; for(int i=head[u];i;i=e[i].next) { int v=e[i].to; if(v==fa) continue; num_son++; dfs1(u,v,dep+1); int temp=t[v].num_to; t[u].num_to+=temp; if(temp>max_to) t[u].wson=v,max_to=temp; } } int id=1; void dfs2(int u,int top) { t[u].top=top; t[u].id=id; color[id]=t[u].w; id++; if(t[u].wson==-1) return; dfs2(t[u].wson,top); for(int i=head[u];i;i=e[i].next) { int v=e[i].to; if(v==t[u].fa||v==t[u].wson) continue; dfs2(v,v); } } struct stree{ int l,r; int lc,rc;//边界l、r的颜色 int num;//区间内色块数 }s[400010]; int lazy[400010]={0};//区间染色lazy void maketree(int x,int l,int r) { s[x].l=l,s[x].r=r; s[x].lc=color[l],s[x].rc=color[r]; if(l==r) { s[x].num=1; return; } int mid=l+r>>1; maketree(x<<1,l,mid); maketree(x<<1|1,mid+1,r); s[x].num=s[x<<1].num+s[x<<1|1].num-(s[x<<1].rc==s[x<<1|1].lc); } void pushdown(int x) { int ls=x<<1,rs=ls|1; s[rs].num=s[ls].num=1; s[ls].lc=s[ls].rc=s[rs].rc=s[rs].lc=lazy[ls]=lazy[rs]=lazy[x]; lazy[x]=0; } int query(int x,int l,int r) { if(l>s[x].r||r<s[x].l) return 0; if(l<=s[x].l&&s[x].r<=r) return s[x].num; if(lazy[x]) pushdown(x); int ans=query(x<<1,l,r)+query(x<<1|1,l,r); if(l<=s[x<<1].r&&r>=s[x<<1|1].l&&s[x<<1].rc==s[x<<1|1].lc) ans--; return ans; } int query_color(int x,int pos) { int l=s[x].l,r=s[x].r; if(l==r) return s[x].lc; int mid=l+r>>1; if(lazy[x]) pushdown(x); if(pos<=mid) return query_color(x<<1,pos); else return query_color(x<<1|1,pos); } void update(int x,int l,int r,int c) { if(l>s[x].r||r<s[x].l) return; if(l<=s[x].l&&s[x].r<=r) { lazy[x]=c; s[x].num=1; s[x].lc=s[x].rc=c; return; } if(lazy[x]) pushdown(x); update(x<<1,l,r,c),update(x<<1|1,l,r,c); s[x].lc=s[x<<1].lc; s[x].rc=s[x<<1|1].rc; s[x].num=s[x<<1].num+s[x<<1|1].num-(s[x<<1].rc==s[x<<1|1].lc); } void C(int x,int y,int c) { while(t[x].top!=t[y].top) { if(t[t[y].top].dep<t[t[x].top].dep) std::swap(x,y);//y的top更深 update(1,t[t[y].top].id,t[y].id,c); y=t[t[y].top].fa; } if(t[y].id<t[x].id) std::swap(x,y); update(1,t[x].id,t[y].id,c); } int Q(int x,int y) { int ans=0; while(t[x].top!=t[y].top) { if(t[t[y].top].dep>t[t[x].top].dep) std::swap(x,y);//x的top更深 ans+=query(1,t[t[x].top].id,t[x].id)-(query_color(1,t[t[x].top].id)==query_color(1,t[t[t[x].top].fa].id)); x=t[t[x].top].fa; } if(t[y].id<t[x].id) std::swap(x,y); ans+=query(1,t[x].id,t[y].id); return ans==0?1:ans; } int main() { //freopen("test.in","r",stdin); scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&t[i].w); for(int i=1,u,v;i<n;i++) { scanf("%d%d",&u,&v); add(u,v); add(v,u); } dfs1(0,1,1); dfs2(1,1); maketree(1,1,n); for(int i=1,a,b,c;i<=m;i++) { char mode[2]; scanf("%s",mode); if(mode[0]=='Q') { scanf("%d%d",&a,&b); printf("%d ",Q(a,b)); } else { scanf("%d%d%d",&a,&b,&c); C(a,b,c); } } return 0; }