在3D中,我们经常涉及到空间坐标系的变换,从模型坐标系到世界坐标系 世界坐标系到摄像机坐标系之类的转换。
1 _ViewPos = worldPos * ViewMatrix;
同样的我们也想到,模型的上的法线是否也可以(有些情况下是正确的)
_ViewNormal = worldNormal * ViewMatrix;
N是物体表面的法线,T是物体表面的切线,垂直于法线
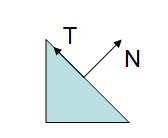
如果在变换矩阵是含有缩放,比如Y轴放大的2倍。我们可以法线方向错误了。
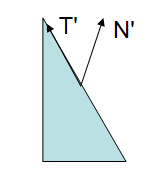
明确一点 向量只含有 方向和强度信息 不包含位置。
如果在变换中,我们只能保证方向的一致性,不能保证位置一致性。那么我们法线该有什么矩阵变换呢。
我们假设,我们T和N垂直,如果正确变换的话,变换后T‘和N’ 也应该垂直。 我们设定法线的变换矩阵G 切线的变换矩阵M
我们把左边式变成 矩阵相乘
(单行矩阵 乘 单列矩阵)
根据矩阵的转置性质
如果
那么
我们就可以得到
矩阵性质里面有说道,如果矩阵是正交矩阵那么
。
所以说有些情况下 可以直接相乘。
参考:http://www.lighthouse3d.com/tutorials/glsl-12-tutorial/the-normal-matrix/