数据结构

主要内容

• 1. 树的概念
• 2. 二叉树
• 3.二叉搜索树
• 4.AVL树
• 5.B树 | B+ 树

1. 树的概念

1.1 简单概述

• 树是一种数据结构 比如：目录结构
• 树是一种可以递归定义的数据结构
• 树是由n个节点组成的集合：
• 如果n=0，那这是一棵空树；
• 如果n>0，那存在1个节点作为树的根节点，其他节点可以分为m个集合，每个集合本身又是一棵树。

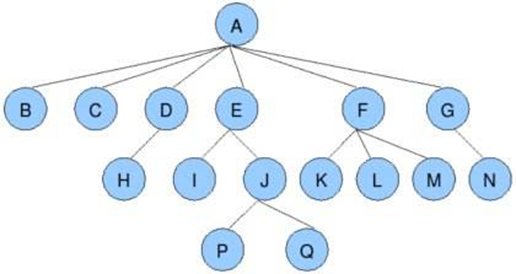
1.2 一些基本的概念

• 根节点、叶子节点 : A 根节点    P,Q是叶子结点
• 树的深度（高度）:  4 共有4层
• 树的度  :任意一个节点有几个叉
• 孩子节点/父节点 : 有上下级关系的节点
• 子树

2. 二叉树

2.1 定义; 度不超过2的树（节点最多有两个叉）

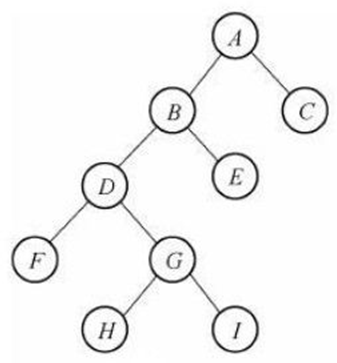
 2.2 两种特殊的二叉树

满二叉树 : 一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。

完全二叉树 : 叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树  

2.3 二叉树的存储方式

 (1) 顺序的存储方式 (列表)  ---- 只限于完全二叉树 ,其他的情况会浪费空间

     

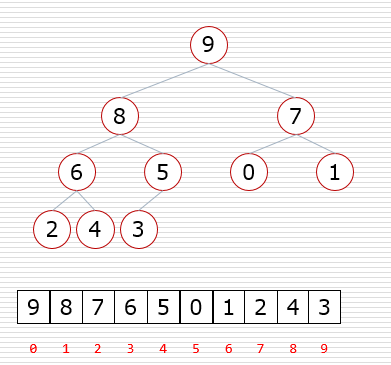
• 父节点和左孩子节点的编号下标有什么关系？0-1 1-3 2-5 3-7 4-9     i  -> 2i+1
• 父节点和右孩子节点的编号下标有什么关系？0-2 1-4 2-6 3-8 4-10   i  -> 2i+2

(2) 链式的存储方式

将二叉树的节点定义为一个对象，节点之间通过类似链表的链接方式来连接

 节点的定义:

class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None
        self.rchild = None

 

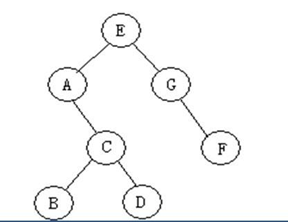
class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None
        self.rchild = None

a = BiTreeNode('A')
b = BiTreeNode('B')
c = BiTreeNode('C')
d = BiTreeNode('D')
e = BiTreeNode('E')
f = BiTreeNode('F')
g = BiTreeNode('G')

e.lchild = a
e.rchild = g
a.rchild = c
c.lchild = b
c.rchild = d
g.rchild = f

root = e

2.3 二叉树的遍历

• 前序遍历 

  # 深度优先搜索 - 前序遍历(先序遍历)   
  def pre_order(root):
      if root: # 如果不是空树
          print(root.data, end='')
          pre_order(root.lchild)
          pre_order(root.rchild)
  
  pre_order(root)   #EACBDGF

  注: 先打印根节点,在递归左右孩子节点,会实现深度优先遍历

• 中序遍历 -> 当用栈来解释,就是每次从左孩子返回,打印该节点

  # 深度优先搜索 - 中序遍历
  def in_order(root):
      if root: # 如果不是空树
          in_order(root.lchild)
          print(root.data, end='')
          in_order(root.rchild)
  
  in_order(root)    #ABCDEGF

  注: 先递归左孩子,再输出自己,再递归右孩子,意味着只有当每一个节点的左孩子全部打印,再打印自己,最后打印右孩子

• 后续遍历

  # 深度优先搜索 - 后序遍历
  def post_order(root):
      if root: # 如果不是空树
          post_order(root.lchild)
          post_order(root.rchild)
          print(root.data, end='')
  
  post_order(root)    #BDCAFGE

  注: 先递归左子树,在递归有子树,最后输出自己   左子树,子树,节点

• 层次遍历

  # 广度优先搜索 - 层次遍历
  def level_order(root):
      q = deque()
      q.append(root)
      while len(q)>0: # 只要队列不空
          n = q.popleft()
          print(n.data, end='')
          if n.lchild:
              q.append(n.lchild)
          if n.rchild:
              q.append(n.rchild)
  
  level_order(root)          #EAGCFBD 

 3. 二叉搜索树

二叉搜索树是一颗二叉树且满足性质：设x是二叉树的一个节点。如果y是x左子树的一个节点，那么y.key ≤ x.key；如果y是x右子树的一个节点，那么y.key ≥ x.key.

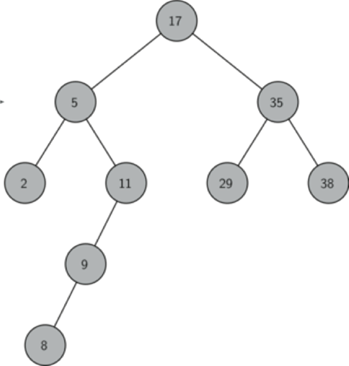
3.1 二叉树的创建 ,插入 ,遍历

class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None
        self.rchild = None


class BST:
    def __init__(self, li):
        self.root = None
        for v in li:
            self.insert(v)

    def insert(self, key):
        if not self.root:
            self.root = BiTreeNode(key)
            return
        p = self.root
        while p:
            if key < p.data:
                if p.lchild: # p有左子树
                    p = p.lchild
                else:
                    p.lchild = BiTreeNode(key)
                    return
            elif key > p.data:
                if p.rchild: # p有右子树
                    p = p.rchild
                else:
                    p.rchild = BiTreeNode(key)
                    return
            else:
                return


    def search(self, key):
        p = self.root
        while p:
            if key < p.data:
                p = p.lchild
            elif key > p.data:
                p = p.rchild
            else:
                return True
        return False


    def in_order(self):
        def _in_order(root):
            if root:  # 如果不是空树
                _in_order(root.lchild)
                print(root.data, end=',')
                _in_order(root.rchild)
        _in_order(self.root)

注: 二叉搜索树的中序遍历是升序,也可以做排序,排序 O(nlogn)  但是占了空间

3.2 二叉搜索树的删除  O(logn)

 如果要删除的是叶子结点,直接删除

 

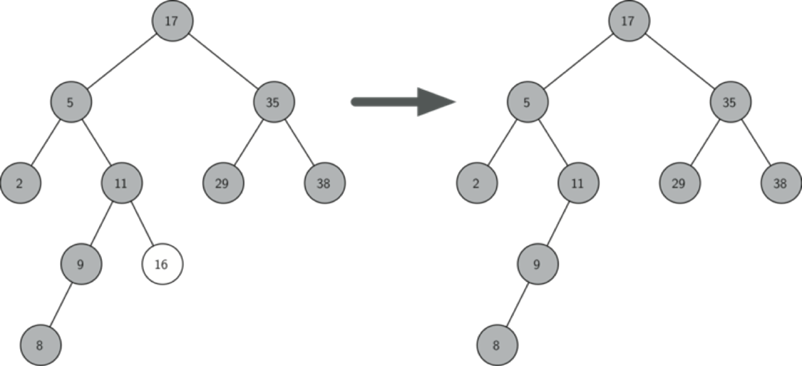
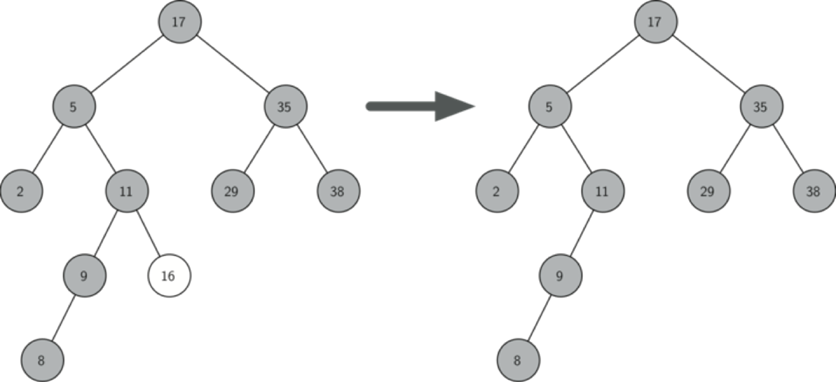
如果要删除的节点只有一个孩子：将此节点的父亲与孩子连接，然后删除该节点

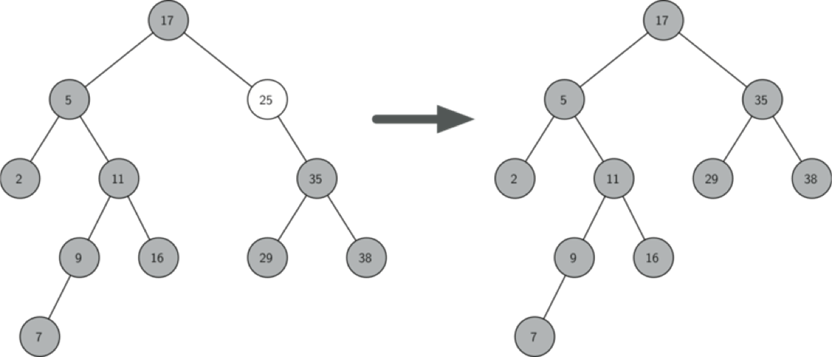
如果要删除的节点有两个孩子：将其右子树的最小节点（该节点最多有一个右孩子）删除，并替换当前节点

3.3 二叉搜索树的效率

• 平均情况下，二叉搜索树进行搜索的时间复杂度为O(nlogn)。
• 最坏情况下，二叉搜索树可能非常偏斜  O(n^2)

解决方案：

• 随机化插入
• AVL树

5. B树 | B+树