Picard 法求方程根

要点:

首先对于任何方程 ：f(x)=0 ，可以转换成 f(x)+x-x => f(x)+x=x;

取g(x)=f(x)+x;  那么 新方程g(x)=x 的解即是 f(x)=0的解，即g(x)-x=0 成立时有 f(x)+x-x=0

现在研究g(x)=x 的解，该方程的解对应 函数 y=g(x) 与 函数y=x的交点(x1,y1)的x坐标即x1.

函数y=x 是对称直线,上面的的任意点(xa,ya)有xa=ya.

picard 方法的具体过程是，选任意x=x0(当然实际上是有条件的，见教程例9), 计算x1=g(x0),x2=g(x1)....xn=g(x_n-1)

当xn稳定在某一值附近时，则xn是方程的解（当然数列x0,x1,x2....xn也可能是发散的，即无法取得解，参考例9的说明）

解方程一般过程，如果可能先画出方程对应的函数，找出过零点（根）然后采用近似根按newton法或picard法进行迭代

matlab代码

clc
clear
syms x;
format long
%g=@(x)(log(x)*1000);
g=@(x)(log(x)-x/1000+x);
x=430;
for i=1:1:20  %迭代步数
   x=g(x);
end
x

 注意上面代码是计算ln(x)/x=1/1000的根 （9121）即方程 ln(x)-x/1000=0 或者 1000ln(x)-x=0;

 迭代时使用的函数g(x)=f(x)+x ，即 g(x)=ln(x)-x/1000+x 或者 g(x)=1000 ln(x) -x +x

选择不同的g(x)迭代过程有区别，见下面的讨论。

实际测试：

采用 g(x)=log(x)-x/1000 +x , g'(x)=1/x +999/1000 可见g'(x)始终接近1，下图看到两条曲线重叠

在采用上面代码迭代时，需要20000步左右才迭代到根附近(9118)

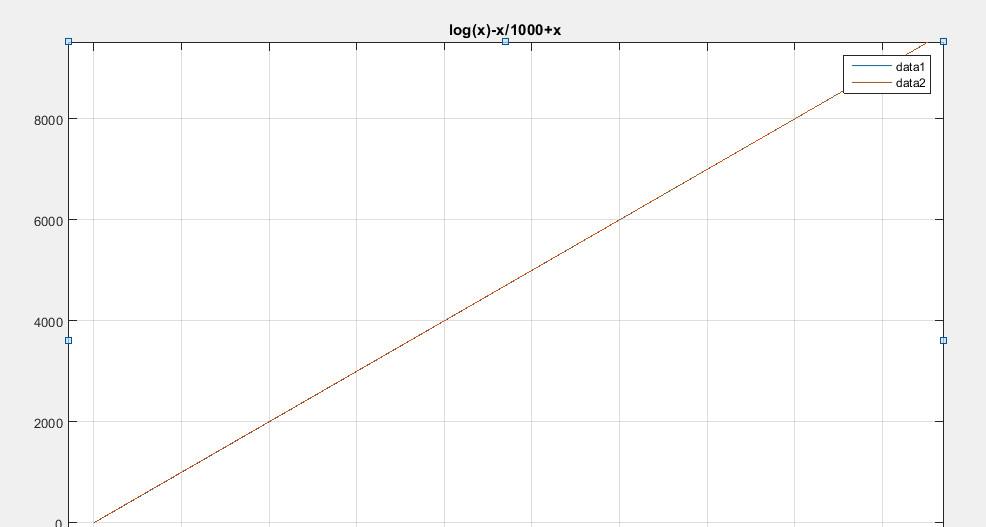
采用g(x)=1000ln(x)-x+x 进行迭代，g'(x)=1000/x 当x增大到10000时导数会取值是0.1,故收敛的过程比较快

迭代过程只需10步即可导9118.xxxx

斜率大于1的曲线不动点可以通过求其反函数的不动点来获取