级数的部分和组成了一个部分和数列,如果这个数列在n->∞ 时有极限,那么我们说级数有极限(收敛converges)反正级数发散(diverges)
级数是数列2维的存在!

首先,绝对收敛级数收敛(或者时说一个级数绝对收敛,那么这个级数收敛)

证明过程
目标,证明

注意下面60题参考答案(a)部分中,选取的ε,在两个等式中是一样的,M是绝对收敛时的极限,L是不带绝对值符号的极限(正常部分和序列的极限)
我们在N1,N2中选择大的那个max{N1,N2}以保证两个等式成立,注意此时ε是任意大于0的实数.
另外还要注意到级数的项数列{an}与级数项取绝对值后组成的数列{|an|},其项数是一样的,(同样两个级数的部分和数列{Sn}也是一样多的项 )
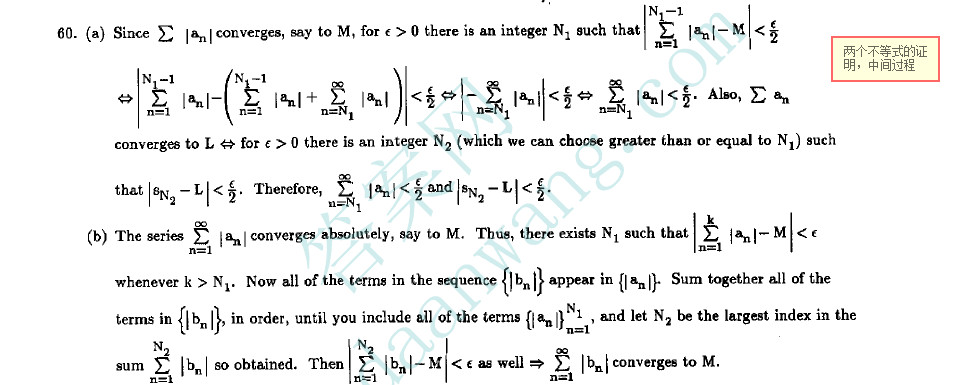
部分(b)的理解:
{|bn|}里面的元素一定都在{|an|}中--重排的定义, 如果选择某个ε>0 根据数列极限定义(部分和数列)有|SUM_1_k |an|-M|<ε --(1式)其中k>=N1,
那么采用{|bn|}的元素想加,一定也能得到|SUM_1_k|bn|-M|<ε --(2式) 其中k>=N2>=N1 , 注意一个收敛级数SUM|an| 当 指标增大(即部分和项标增大时),
或者说加上更多的项时其与M是越来越近的(因为部分和数列是非减有上限的,单调增),所以满足1式的ε一定也满足2式。


关于(SUM_1_k bn - SN2)的值 其中k>=N3 :
应该是有限数列{xn},该数列有N3-N2+1 个项,里面元素是不属于{a1-aN2}的{an}中的元素的某个重排相加
这个值是小于{|aN1|+...|an|} 但是 与 (SUM_1_∞ bn - SN2) 之间无法比较大小,所以 书上可能是错误了(上图)
