柯西-古萨定理以及推论

单连通区域：

    闭围道包围的区域里被积函数处处解析（不存在奇点)那么积分是0，

多连通区域：

  闭围道包围的区域里有奇点存在，积分不一定是0，当然也有0的如  f(z)=  (z-z0)^n-1  在n= +-1, +-2.... 是围道  |z-z0|=R时积分就是0

  n取 -1时f(z)=1/  (z-z0)   z0是被积函数的奇点，而且奇点包围在围道构成的区域里，积分是0

  对 f(z)=1/z   ,z=0是奇点， 对任意|Z|=R 的轨道，由于包含奇点，所以积分是相同的，如果去z=re(i*theta) +z0 ,并且控制半径r使包围的区域不含原点，那么积分是0

 

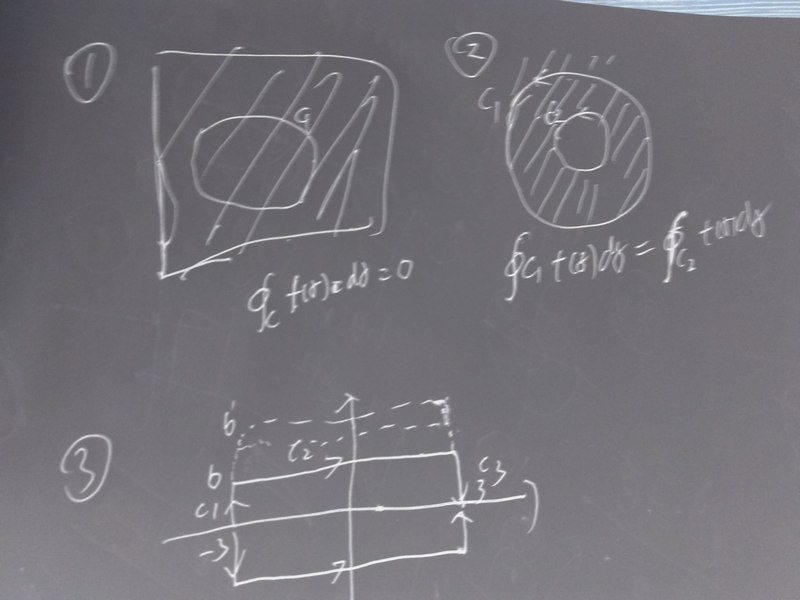
一些函数的讨论:

  被积函数 f(z)=z^1/2  从-3到3的积分，选择如图(3)轨道

clc
clear
syms x y theta
b=5;
z_c1=-3+y*i; %0,b
z_c2=x+b*i;  %-3,3
z_c3_=3+y*i; %0,b

c1= int( z_c1^(0.5) * diff(z_c1,y),y,0,b);
c2= int( z_c2^(0.5) * diff(z_c2,x),x,-3,3);
c3= -int( z_c3_^(0.5) * diff(z_c3_,y),y,0,b);
b
c=c1+c2+c3
dc= double(c)

z_r=3*exp(i*theta);
c=int(z_r^(0.5)*diff(z_r,theta),theta,0,2*pi)
cc=double(c)
double(-4*i*sqrt(3))

clc
clear

syms x y
b=-14; %b<0
z_c1_=-3+y*i; %b,0
z_c2=x+b*i;  %-3,3
z_c3=3+y*i; %b,0

c1= -int( z_c1_^(0.5) * diff(z_c1_,y),y,b,0);
c2= int( z_c2^(0.5) * diff(z_c2,x),x,-3,3);
c3= int( z_c3^(0.5) * diff(z_c3,y),y,b,0);
b
c=c1+c2+c3
dc= double(c)

上两段代码结论:改变b的取值，积分不变。

clc
clear

syms x y theta
r=3; %r>0
z_c=r*exp(i*theta);
c=int( (z_c)^(0.5) * diff(z_c,theta),theta,0,2*pi)
double(c)

采用圆形轨道-正方向，r=3时结果跟上面一样，当r取其他值时，积分不一样，表明不同r构成的环形区域里z^(1/2)不解析--有奇点。

在matlab主支 取  -pi到pi ，所以在负实轴与原点，函数不解析

z^1/2 可转化成   e^(ln(z^(1/2)))= e^(0.5 * ln(z)) 由于 log(z)在0与负实轴上不解析，所以z^(0.5)也一样

 被积函数 f(z)=1/z  做圆心在原点或者在z0点的封闭轨道

clc
clear

syms x y theta
r=rand(1)*100; %r>0
z_c=r*exp(i*theta);
z0=r+i*r;
z_c2=(r*sqrt(2) +1)*exp(i*theta) + z0;
r
c=int( z_c^(-1) * diff(z_c,theta),theta,0,2*pi)
c2=int( z_c2^(-1) * diff(z_c2,theta),theta,0,2*pi)

 圆点在原点时，各种半径的圆积分都是一样的， 当原点在z0是，圆包围区域如果不包括原点，那积分都是0，也就是单连通区域的情况

被积函数 f(z)=log(z+2) 做圆心在原点的积分

clc
clear

syms x y theta
r=5; %r>0
z0=2;
z_c=r*exp(i*theta);


r
c=int( log(z_c+z0) * diff(z_c,theta),theta,0,2*pi)
double(c)

明显log(0)因为为要取ln(0) + i*theta 所以0是奇点， log(z+2)可看成被积函数是log(z) 而轨道是 z=1*e^(i*theta) + 2 , 可见半径是1，圆心在(2,0)避开了原点，所以积分是0

但是当r取大于2时就包括了原点，所以积分就不为零0，而且发现随着r变大积分也改变，表明环形区域里也存在奇点。

clear

syms x y theta
r=2; %r>0
z0=-3;
z_c=r*exp(i*theta)+z0;


r
c=int( log(z_c) * diff(z_c,theta),theta,0,2*pi)
double(c)

log 主支是取 -pi<a<pi, matlab中，积分半径为1，圆心在负实轴上的路径，结果不为零，半径不同积分各不相同，参考复变与积分变换参考书 45页

几道练习

  

tan(z)奇点的出现的周期是 pi/2 + npi, 采用matlab发现在r取pi/2 到 pi/2 + pi之间是，积分一致，说明环形区域内没有奇点了。