python机器学习-乳腺癌细胞挖掘(博主亲自录制视频)
https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share
sklearn:multiclass与multilabel,one-vs-rest与one-vs-one
针对多类问题的分类中,具体讲有两种,即multiclass classification和multilabel classification。multiclass是指分类任务中包含不止一个类别时,每条数据仅仅对应其中一个类别,不会对应多个类别。multilabel是指分类任务中不止一个分类时,每条数据可能对应不止一个类别标签,例如一条新闻,可以被划分到多个板块。
无论是multiclass,还是multilabel,做分类时都有两种策略,一个是one-vs-the-rest(one-vs-all),一个是one-vs-one。这个在之前的SVM介绍中(http://blog.sina.com.cn/s/blog_7103b28a0102w07f.html)也提到过。
在one-vs-all策略中,假设有n个类别,那么就会建立n个二项分类器,每个分类器针对其中一个类别和剩余类别进行分类。进行预测时,利用这n个二项分类器进行分类,得到数据属于当前类的概率,选择其中概率最大的一个类别作为最终的预测结果。
在one-vs-one策略中,同样假设有n个类别,则会针对两两类别建立二项分类器,得到k=n*(n-1)/2个分类器。对新数据进行分类时,依次使用这k个分类器进行分类,每次分类相当于一次投票,分类结果是哪个就相当于对哪个类投了一票。在使用全部k个分类器进行分类后,相当于进行了k次投票,选择得票最多的那个类作为最终分类结果。
在scikit-learn框架中,分别有sklearn.multiclass.OneVsRestClassifier和sklearn.multiclass.OneVsOneClassifier完成两种策略,使用过程中要指明使用的二项分类器是什么。另外在进行mutillabel分类时,训练数据的类别标签Y应该是一个矩阵,第[i,j]个元素指明了第j个类别标签是否出现在第i个样本数据中。例如,np.array([[1, 0, 0], [0, 1, 1], [0, 0, 0]]),这样的一条数据,指明针对第一条样本数据,类别标签是第0个类,第二条数据,类别标签是第1,第2个类,第三条数据,没有类别标签。有时训练数据中,类别标签Y可能不是这样的可是,而是类似[[2, 3, 4], [2], [0, 1, 3], [0, 1, 2, 3, 4], [0, 1, 2]]这样的格式,每条数据指明了每条样本数据对应的类标号。这就需要将Y转换成矩阵的形式,sklearn.preprocessing.MultiLabelBinarizer提供了这个功能。
ons-vs-all的multiclass例子如下:
one-vs-one的multiclass例子如下:
https://www.cnblogs.com/taceywong/p/5932682.html
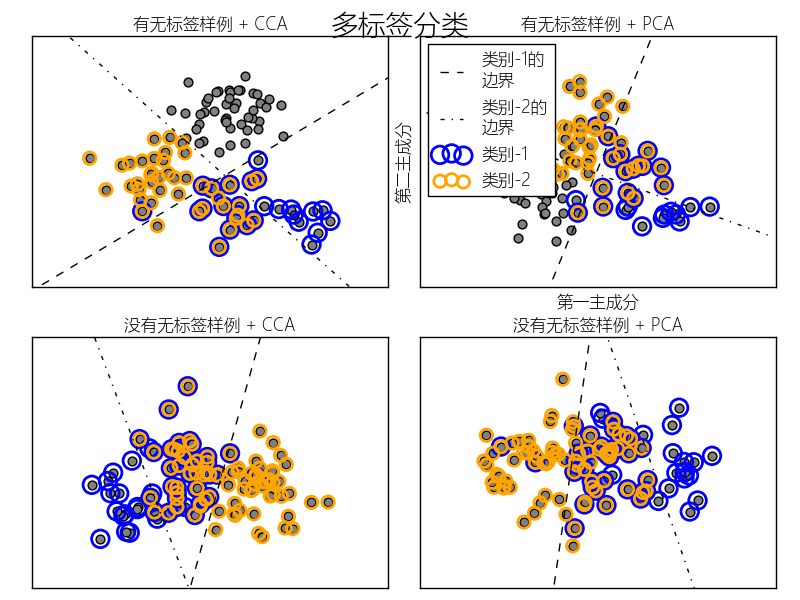
本例模拟一个多标签文档分类问题.数据集基于下面的处理随机生成:
- 选取标签的数目:泊松(n~Poisson,n_labels)
- n次,选取类别C:多项式(c~Multinomial,theta)
- 选取文档长度:泊松(k~Poisson,length)
- k次,选取一个单词:多项式(w~Multinomial,theta_c)
在上面的处理中,拒绝抽样用来确保n大于2,文档长度不为0.同样,我们拒绝已经被选取的类别.被同事分配给两个分类的文档会被两个圆环包围.
通过投影到由PCA和CCA选取进行可视化的前两个主成分进行分类.接着通过元分类器使用两个线性核的SVC来为每个分类学习一个判别模型.注意,PCA用于无监督降维,CCA用于有监督.
注:在下面的绘制中,"无标签样例"不是说我们不知道标签(就像半监督学习中的那样),而是这些样例根本没有标签~~~
# coding:utf-8
import numpy as np
from pylab import *
from sklearn.datasets import make_multilabel_classification
from sklearn.multiclass import OneVsRestClassifier
from sklearn.svm import SVC
from sklearn.preprocessing import LabelBinarizer
from sklearn.decomposition import PCA
from sklearn.cross_decomposition import CCA
myfont = matplotlib.font_manager.FontProperties(fname="Microsoft-Yahei-UI-Light.ttc")
mpl.rcParams['axes.unicode_minus'] = False
def plot_hyperplane(clf, min_x, max_x, linestyle, label):
# 获得分割超平面
w = clf.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(min_x - 5, max_x + 5) # 确保线足够长
yy = a * xx - (clf.intercept_[0]) / w[1]
plt.plot(xx, yy, linestyle, label=label)
def plot_subfigure(X, Y, subplot, title, transform):
if transform == "pca":
X = PCA(n_components=2).fit_transform(X)
elif transform == "cca":
X = CCA(n_components=2).fit(X, Y).transform(X)
else:
raise ValueError
min_x = np.min(X[:, 0])
max_x = np.max(X[:, 0])
min_y = np.min(X[:, 1])
max_y = np.max(X[:, 1])
classif = OneVsRestClassifier(SVC(kernel='linear'))
classif.fit(X, Y)
plt.subplot(2, 2, subplot)
plt.title(title,fontproperties=myfont)
zero_class = np.where(Y[:, 0])
one_class = np.where(Y[:, 1])
plt.scatter(X[:, 0], X[:, 1], s=40, c='gray')
plt.scatter(X[zero_class, 0], X[zero_class, 1], s=160, edgecolors='b',
facecolors='none', linewidths=2, label=u'类别-1')
plt.scatter(X[one_class, 0], X[one_class, 1], s=80, edgecolors='orange',
facecolors='none', linewidths=2, label=u'类别-2')
plot_hyperplane(classif.estimators_[0], min_x, max_x, 'k--',
u'类别-1的
边界')
plot_hyperplane(classif.estimators_[1], min_x, max_x, 'k-.',
u'类别-2的
边界')
plt.xticks(())
plt.yticks(())
plt.xlim(min_x - .5 * max_x, max_x + .5 * max_x)
plt.ylim(min_y - .5 * max_y, max_y + .5 * max_y)
if subplot == 2:
plt.xlabel(u'第一主成分',fontproperties=myfont)
plt.ylabel(u'第二主成分',fontproperties=myfont)
plt.legend(loc="upper left",prop=myfont)
plt.figure(figsize=(8, 6))
X, Y = make_multilabel_classification(n_classes=2, n_labels=1,
allow_unlabeled=True,
random_state=1)
plot_subfigure(X, Y, 1, u"有无标签样例 + CCA", "cca")
plot_subfigure(X, Y, 2, u"有无标签样例 + PCA", "pca")
X, Y = make_multilabel_classification(n_classes=2, n_labels=1,
allow_unlabeled=False,
random_state=1)
plot_subfigure(X, Y, 3, u"没有无标签样例 + CCA", "cca")
plot_subfigure(X, Y, 4, u"没有无标签样例 + PCA", 
