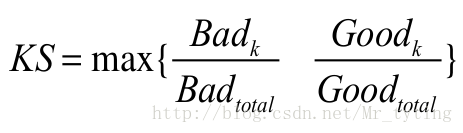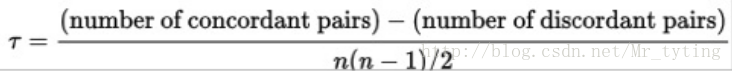python信用评分卡建模(附代码,博主录制)
从这篇博文开始,我将总结金融风控中的另外一个模型:申请评分卡模型。这篇博文将主要来介绍申请评分卡的一些基本概念。
本篇博文将以以下四个主题来进行介绍说明:
- 信用风险和评分卡模型的基本概念
- 申请评分卡在互联网金融业的重要性和特性
- 贷款申请环节的数据介绍和描述
- 非平衡样本问题的定义和解决方法
信用风险和评分卡模型的基本概念
什么是信用风险
交易对手未能履行约定契约中的义务而造成经济损失的风险,即受信人不能履行还本付息的责任而使授信人的预期收益与实际收益发生偏离的可能性它是金融风险的主要类型。
坏样本的定义
- M3 & M3+ 逾期
- 债务重组
- 个人破产
- 银行主动关户或注销
- 其他相关违法行为
M0,M1,M2的定义
- M0:最后缴款日的第二天到下一个账单日
- M1:M0时段的延续,即在未还款的第二个账单日到第二次账单的最后缴款日之间
-
M2:M1的延续,即在未还款的第三个账单日到第三次账单的最后缴款日之间
信用卡账单日是指发卡银行每月会定期对你的信用卡账户当期发生的各项交易,费用等进行汇总结算,并结计利息,计算你的当期总欠款金额和最小还款额,并为你邮寄账单,此日期即为账单日。而还款日则是指信用卡发卡银行要求持卡人归还应付款项的最后日期。
简单点说,银行会对你的当期应还款形成账单并通知你,账单形成日即为账单日,同时,银行不会要求你马上就还款,而是会给你一个缓冲期,通常是20天(具体根据各银行制定标准),该期限截止日即为还款到期日。这20天之内全额还款或是选择信用卡最低还款额方式还款,可以享受免息待遇,但如果逾期,就会计息了。
什么是评分卡
信贷场景中的评分卡
- 以分数的形式来衡量风险几率的一种手段
- 是对未来一段时间内违约/逾期/失联概率的预测
- 有一个明确的(正)区间
- 通常分数越高越安全
- 数据驱动(搜集数据,对数据研究,建立模型)
-
反欺诈评分卡、申请评分卡(Application)、行为评分卡(Behavior)、催收评分卡(Collection)
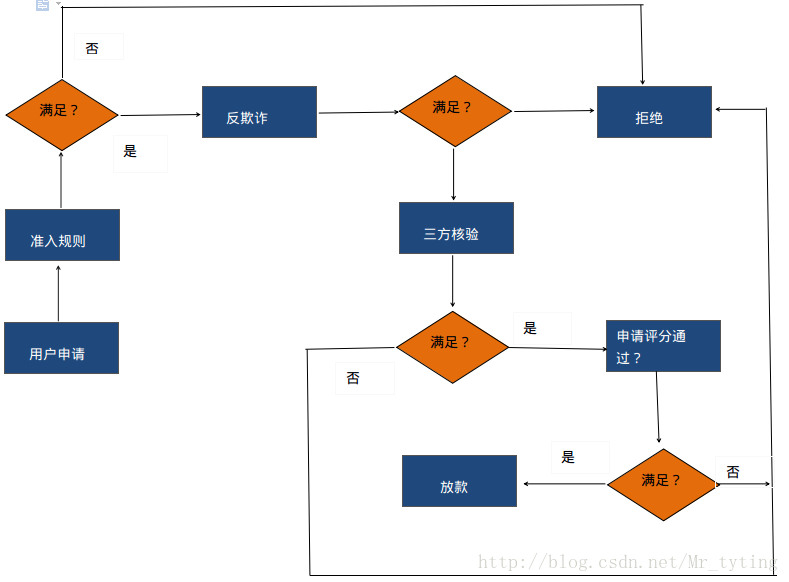
①反欺诈评分卡、申请评分卡是在贷前准入环节里面
②申请评分卡用到的大部分是申请者的背景变量,而且这个模型一般也会比较谨慎。
③行为评分卡表示申请者已经获准贷款,已经放出贷款以后,根据贷款人的消费习惯,还款情况等一些信用特征,就是跟踪客户合同开始后的表现,来预估用户逾期或者是违约概率。
④催收评分卡是对已经逾期或者违约的客户,对他进行一个催收评分,严格来讲,有三个模型,还款率模型,账龄滚动模型,失联模型。
本篇博文主要讲的是申请评分卡模型。
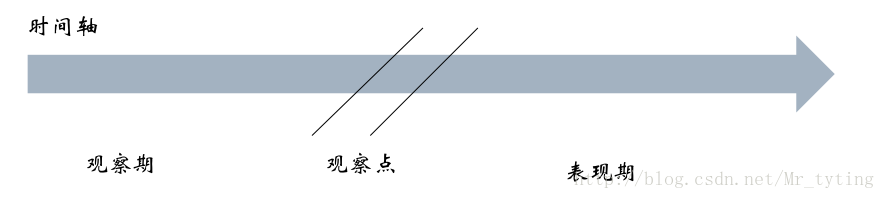
观察期与表现期
观察期
- 搜集变量、特征的时间窗口,通常3年以内
- 带时间切片的变量(比如过去半年还款情况;过去每个月最大还款额等带时间切片的特征)
表现期
搜集是否触发坏样本定义的时间窗口,通常6个月~1年
需要对这张图进行一个详细的说明,观察点不一定是哪一天,可以是一段时间内,在某个时间区间内所有申请人,只要他们观察期和表现期相同即可。举例来说,当一个申请人在2017-7-14号这天来银行申请贷款,银行需要用已有的模型对申请人进行一个申请评分,评估他未来一年(表现期)内违约或者是逾期的概率,然后决定是否放贷。那么这个已有的模型是什么时候建立的呢?这里我们假定观察期为三年,因为上面是评估一年所以这里表现期为一年,那么往前推一年为2016-7-14号左右某个时间区间内作为观察点,再往前推三年(即观察期:2013-7-14到2016-7-14),利用这三年所有观察点内申请人一些信息建立模型的观察变量(即特征),然后再往后推一年(即表现期:2016-7-14到2017-7-14),所有在观察点内的申请人在这一年时间内的表现情况来定义违约。然后来训练出一个模型。对2017-7-14号的申请人进行评分。所以申请评分卡模型有着天然的滞后性,需要不断的对其模型进行监控。
评分卡模型开发步骤
-
立项
-
数据准备与预处理
银行自有数据和第三方数据 -
模型构建
假设模型训练集的观察点(即客户的申请时间段)为2016-01到2016-03,那么这个模型的观察期(这里我们假定为三年)为2013-01到2016-01,模型的表现期(这里我们假定为一年)为2016-03到2017-03。 -
模型评估
对照上面的模型构建的时间来,我们来建立测试集,假定其测试集观察点(即客户的申请时间段)为(2017-04),同理可得观察期,和表现期真实的违约或者逾期与否。这时把模型放在这个测试集上进行测试看看效果如何。这里需要注意训练集和测试集上用户在表现期的表现如何都是基于一个已经发生的时间段上。
模型评估的几个标准在下面会详细说到。 - 验证/审计
实施人跟上面不一样,文档撰写等
-
模型部署
新旧模型替换,评分卡的实时性要求没那么高,在银行通常一个月更新一次模型。有些咨询机构可能一天更新一次评分卡模型。 -
模型监控
跟踪模型各项性能是否发生弱化。
评分卡开发的常用模型
-
逻辑回归
优点: 简单,稳定,可解释,技术成熟,易于监测和部署
缺点:准确度不高 -
决策树
优点: 对数据质量要求低,易解释
缺点:准确度不高 -
其他元模型
-
组合模型
优点: 准确度高,不易过拟合
缺点:不易解释;部署困难;计算量大
模型监控的指标
AR(Accuracy Ratio)
衡量分数预测能力的指标 ,需要一个完整的表现期。看看这个模型能不能把坏样本很好的区分处理。其取值位于-1~1之间。具有滞后性。
如果我们今天用AR来监控模型的好坏,那么只能是监控模型在一年(这里假定表现期为一年)之前的数据上表现的好坏。
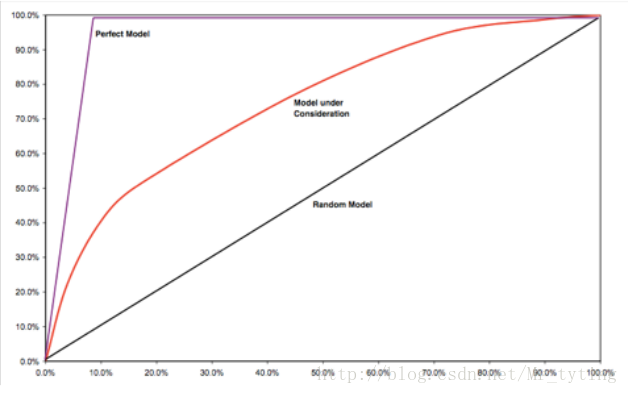
先把样本按分数由低到高排序,X轴是总样本的累积比例,Y轴是坏样本占总的坏样本的累积比例。AR就是等于模型在随机模型之上的面积除以理想模型在随机模型之上的面积。计算中可以用梯形近似逼近曲线下面积来计算,AR越高说明模型区分效果越好。
下图公式中Xk,Yk代表分数的第K个分位点对应的累积总样本及相应的坏样本的比例。设总的坏样本的比例为Bo,令(Xk,Yk)=(0,0)
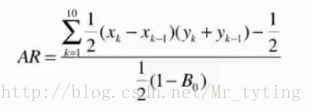
KS(Kolmogorov-Smirnov)
衡量分数区分能力的指标。 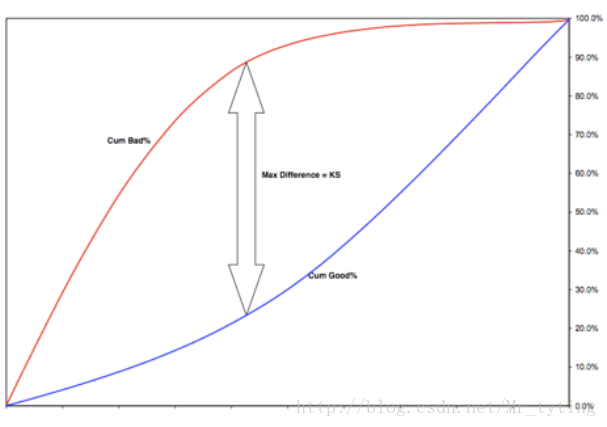
把样本按分数由低到高排序,X轴是总样本累积比例,Y是累积好,坏样本分别占总的好,坏样本的比例。两条曲线在Y轴方向上的相差最大值即KS。KS越大说明模型的区分能力越好。
Bad k和Good k分别表示为分数累积到第k个分位点的坏样本个数和好样本个数,KS计算公式:
PSI( Population Stablility Index)
衡量分数稳定性的指标
按分数对人群进行分组,令Ri是现在样本中第i组占总样本的百分比,Bi是一段时间后第i个分组占总样本的百分比。PSI取值越小说明分数的分布随时间变化越小。
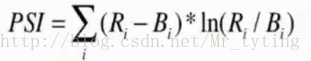
Kendall’s Tau
正确有效的评分卡模型中,低分数的实际逾期率应该严格大于高分段的实际逾期率。我们将分数从低到高划分为10组,每组的实际逾期率记做r1,r2,r3,…,r10。对所有的(ri,rj)的组合,如果有ri< rj且i< j,或者ri> rj且i> j,则记做一个discordant pair,否则记做concordant pair。其计算公式如下:
Kendall’s Tau越接近1或者等于1,说明逾期率在分数上的单调下降性越明显,反之说明分数变化与逾期率的变化的一致性得不到保证。
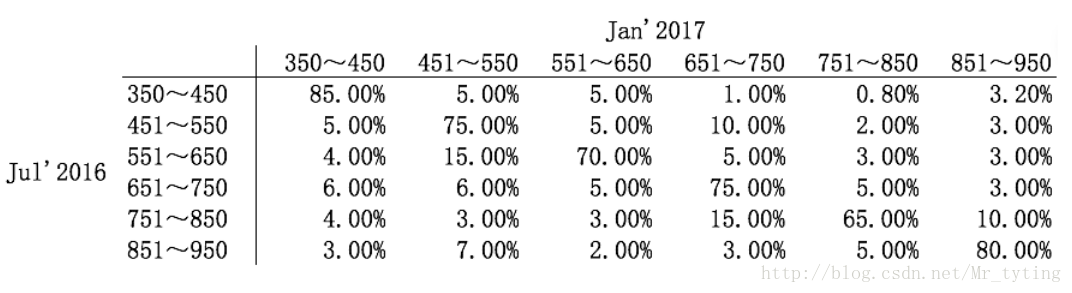
Migration Matrix
迁移矩阵是衡量分数矩阵的指标,对相同的人群,观察在相邻两次监控日期(一周)分数的迁移变化。迁移矩阵中元素Mjk代表上次监控日期分数在第j组中的人群在当前迁移到第k组的概率。实际计算中可把分数平均分成10组,计算这10组之间的迁移矩阵。
申请评分卡的重要性和特性
互联网金融特性与产品
-
传统金融机构+非金融机构
-
传统金融机构: 传统金融业务的互联网创新以及电商化创新、APP软件等
- 非金融机构:利用互联网技术进行金融运作的电商企业
(P2P)模式的网络借贷平台
众筹模式的网络投资平台
挖财类(模式)的手机理财APP(理财宝类)
第三方支付平台等。
为什么要开发申请评分卡
- 风险控制
- 营销
- 资本管理
评分卡的特性
- 稳定性
- 区分性
- 预测能力
- 和逾期概率等价(即评分和逾期率呈相关性)
贷款申请环节的数据介绍和描述
申请评分卡常用的特征
个人信息 : 学历 性别 收入
负债信息 : 在本金融机构或者其他金融机构负债情况
消费能力 : 商品购买纪录,出境游,奢侈品消费
历史信用记录 : 历史逾期行为
新兴数据 : 人际社交 网络足迹 出行 个人财务
非平衡样本问题的定义和解决方法
非平衡样本的定义
在分类问题中,每种类别的出现概率未必均衡
信用风险:正常用户远多于逾期/违约用户
流失风险: 留存客户多于流失客户
非平衡样本的隐患
降低对少类样本的灵敏性
非平衡样本的解决方案
过采样
- 优点: 简单,对数据质量要求不高
- 缺点: 过拟合
欠采样
- 优点: 简单,对数据质量要求不高
- 缺点: 丢失重要信息
SMOTE(合成少数过采样技术)
- 优点: 不易过拟合,保留信息
- 缺点: 不能对有缺失值和类别变量做处理
python风控建模实战lendingClub(博主录制,catboost,lightgbm建模,2K超清分辨率)
https://study.163.com/course/courseMain.htm?courseId=1005988013&share=2&shareId=400000000398149
扫描和关注博主二维码,学习免费python视频教学资源