使用链表实现栈:
前言:
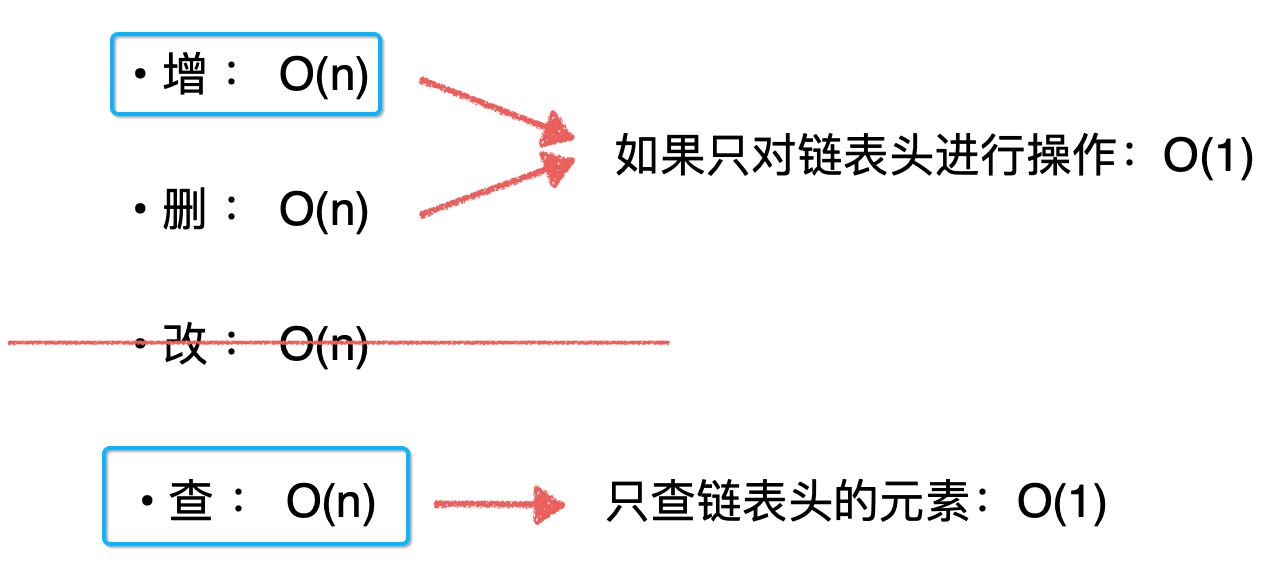
在上一次https://www.cnblogs.com/webor2006/p/15319904.html咱们完成了链表的底层实现,其中对已实现的链表时间复杂度进行了一个分析,有这么一个图:
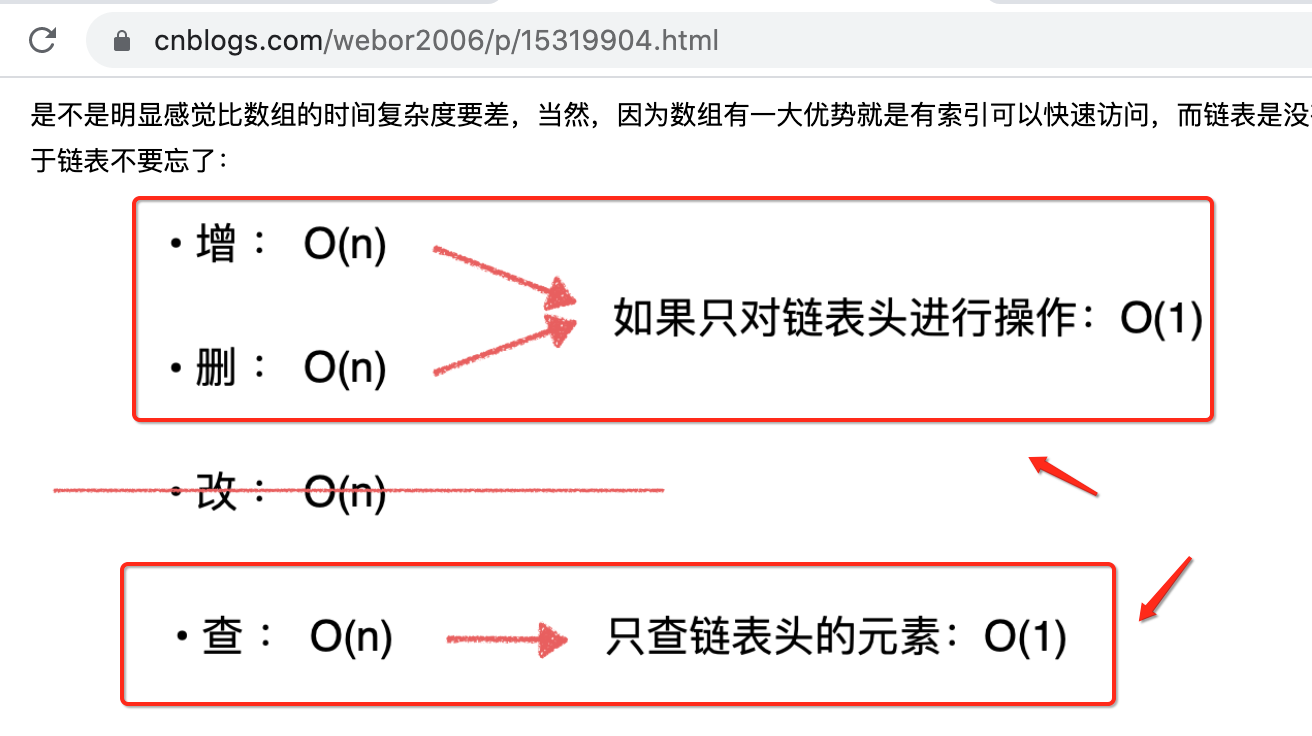
其中只对链表“头”进行增、删、查操作,整个链表的时间复杂度是O(1),也就是性能是非常好的,这里将“头”特意强调的原因是:栈这个数据结构不就是只对头进行操作么?回忆一下栈这个数据结构的特点:后进先出,是不是往栈中增、删、查操作都是从栈顶操作的?关于栈顶和栈底这里需要再复习一下https://www.cnblogs.com/webor2006/p/14216904.html,特别容易搞混:
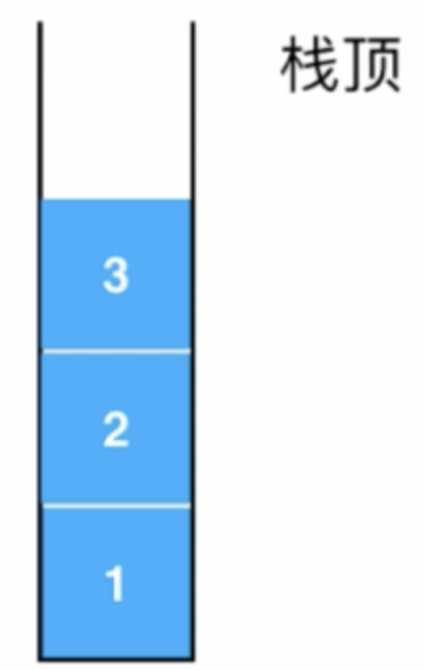
那,是不是咱们完全可以使用链表这个数据结构来构建一个栈?是的,我们只要将链表头当作栈顶就可以很轻松的来实现了,接下来完成这项任务。
实现:
1、将实现的链表类拷进栈实验工程:
回到之前学习编写的栈工程中:

既然要使用链表来实现栈,先将咱们实现的链表这个类拷进工程里来:
2、新建LinkedListStack:
在之前咱们是使用了数组来构建的Stack,其类名命名为:
那对于这次使用链表来说,则是:
而对于原来ArrayStack是实现了Stack这个抽象接口的:
同样的,对于这次要链表栈也得实现:

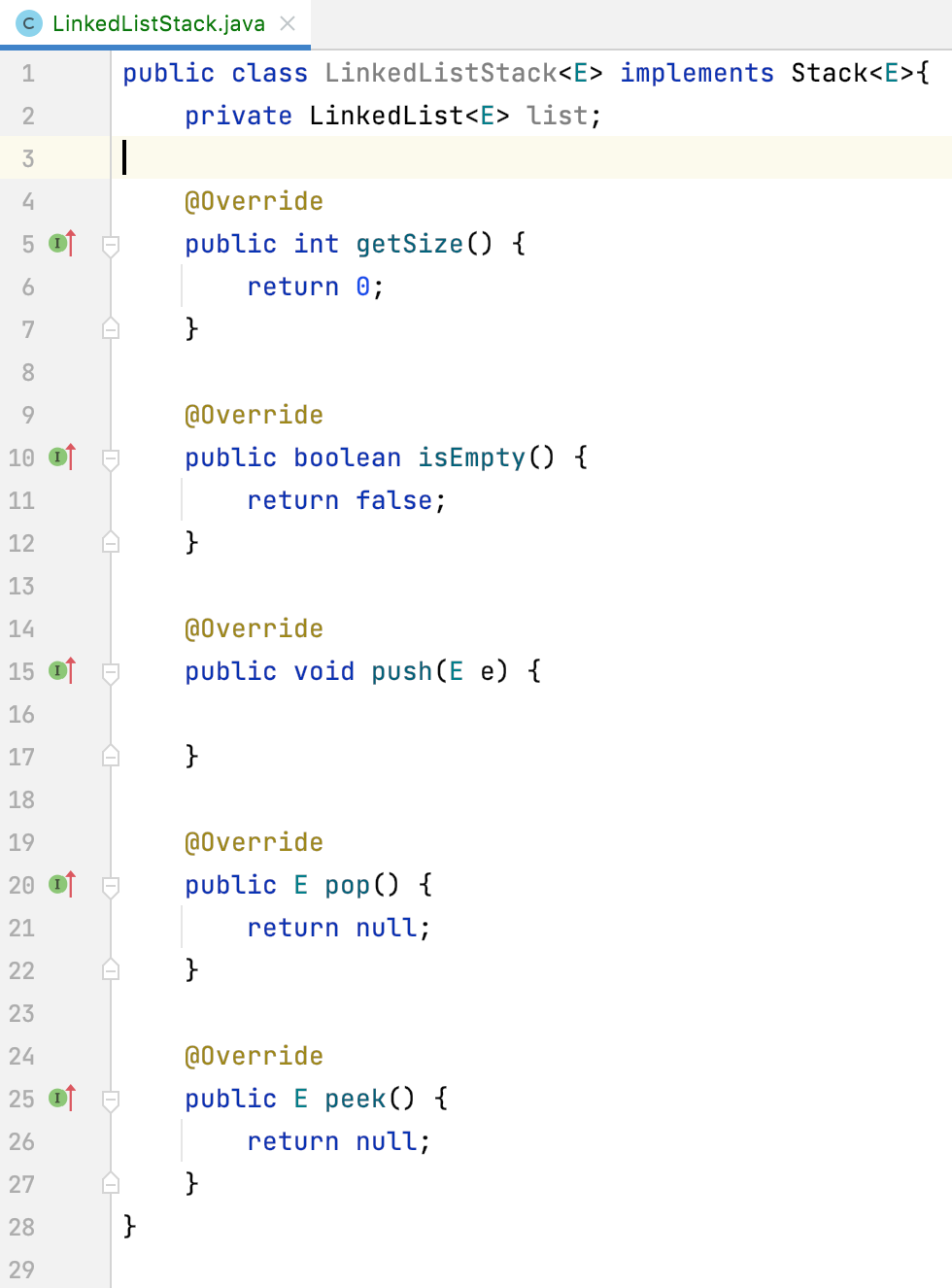
3、构造函数:
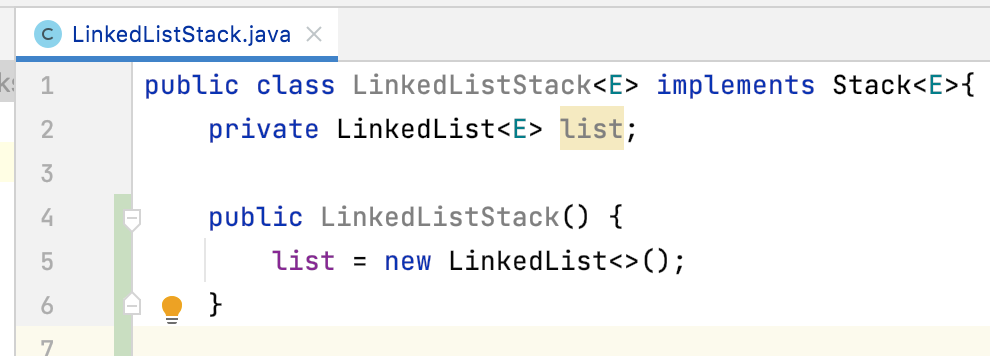
对于链表来说,没容积这个概念了,所以其构造就初始化一下list既可。
4、getSize()、isEmpty():
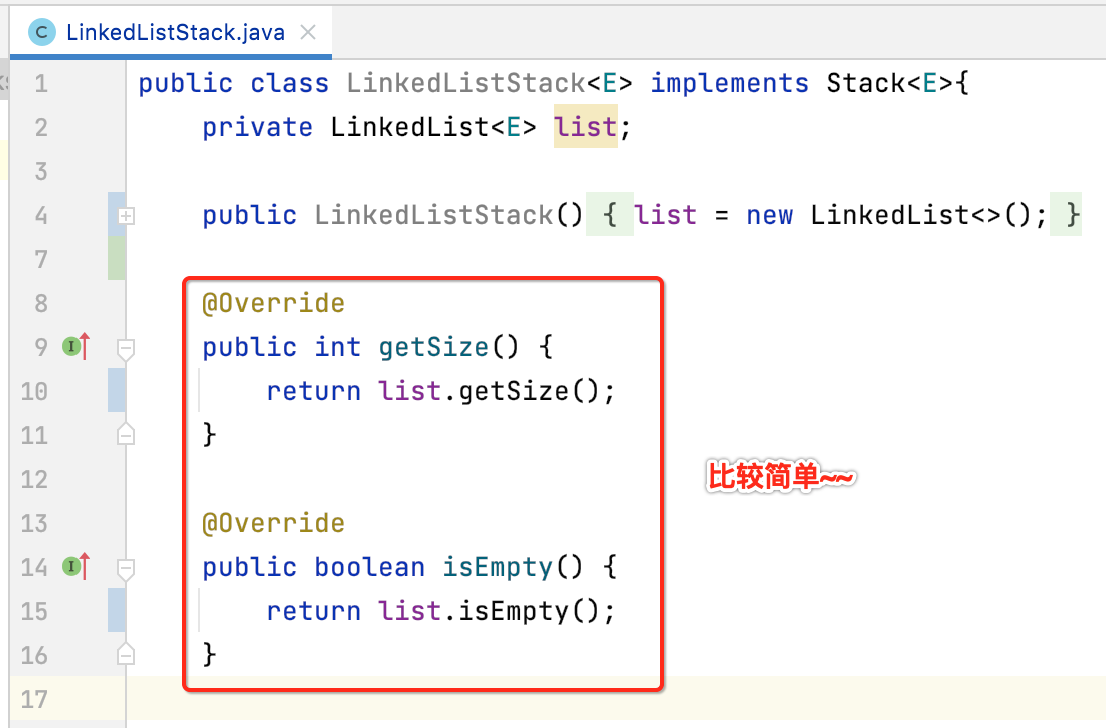
5、push、pop、peek:
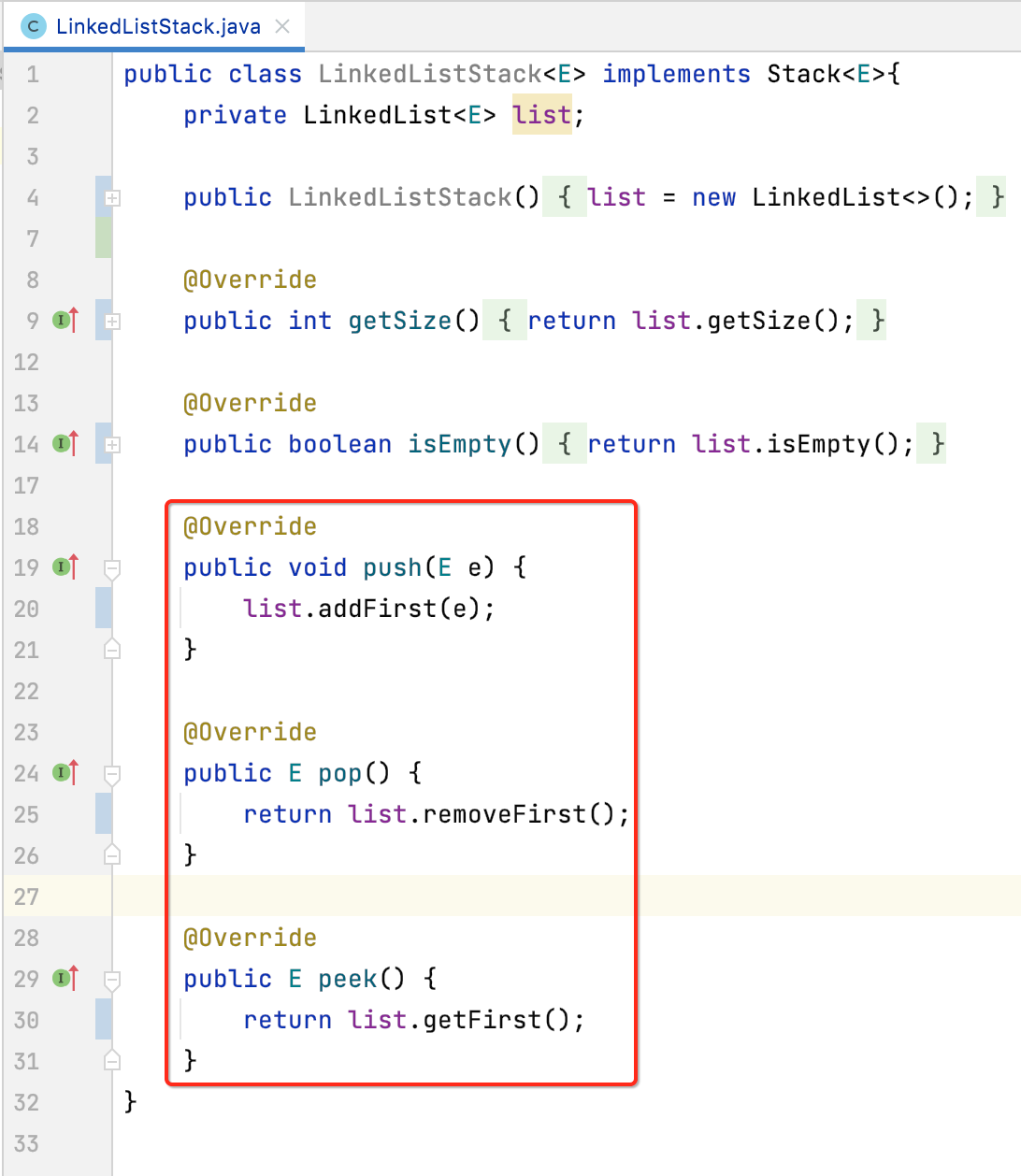
6、toString():
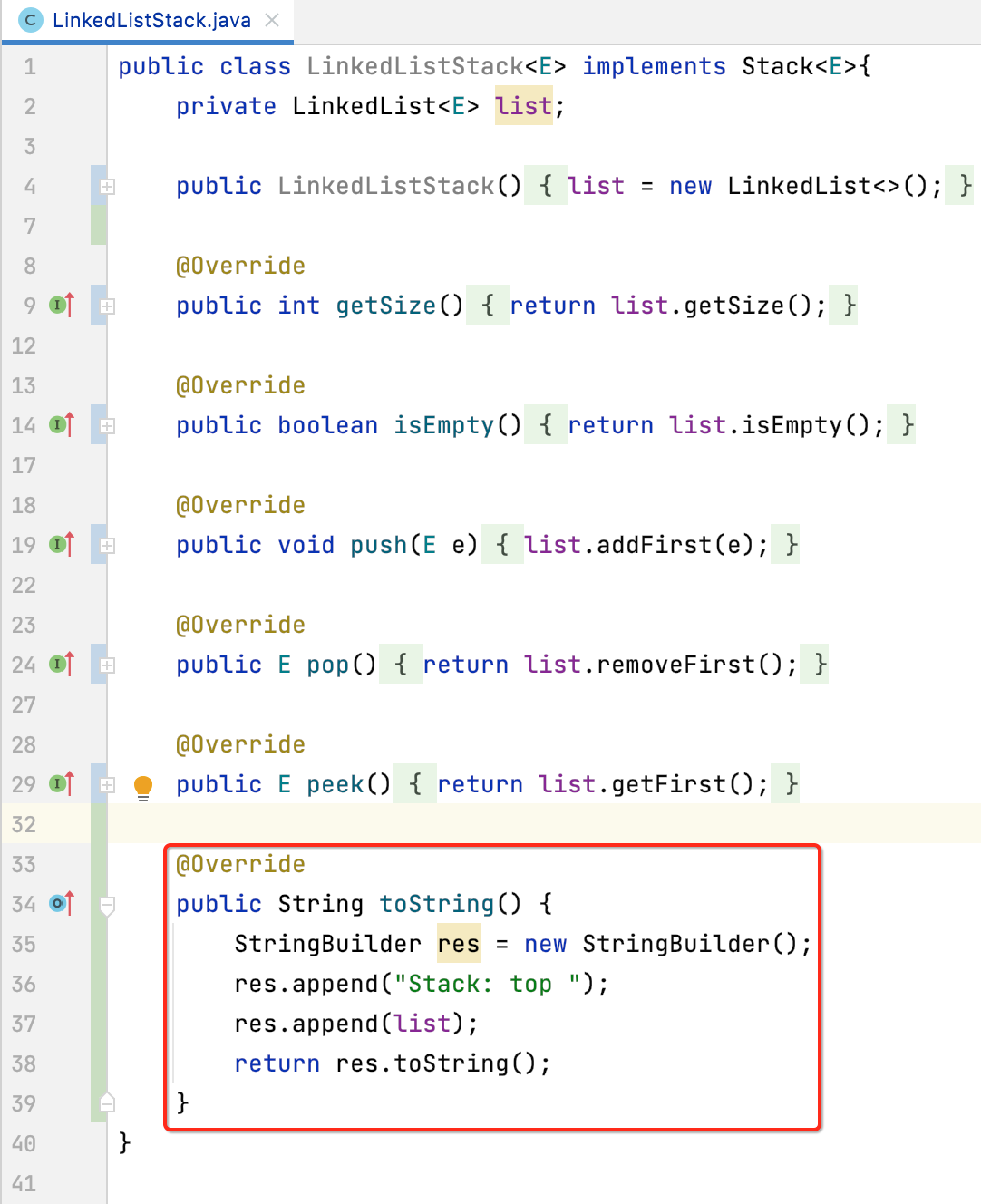
7、运行:
接下来编写一个main()方法来测试一下,其测试用例还是用原来数组实现的栈那块的:

嗯,木问题。
8、测试两者实现的性能:
目前咱们已经有两个实现栈的版本了,一个是数组实现的,一个是链表实现的,那这俩运行的性能差异又是怎样的呢?下面编写一个测试用例来看一下,其编写的风格跟最开始https://www.cnblogs.com/webor2006/p/13914100.html学习线性查找法性能测试类似:
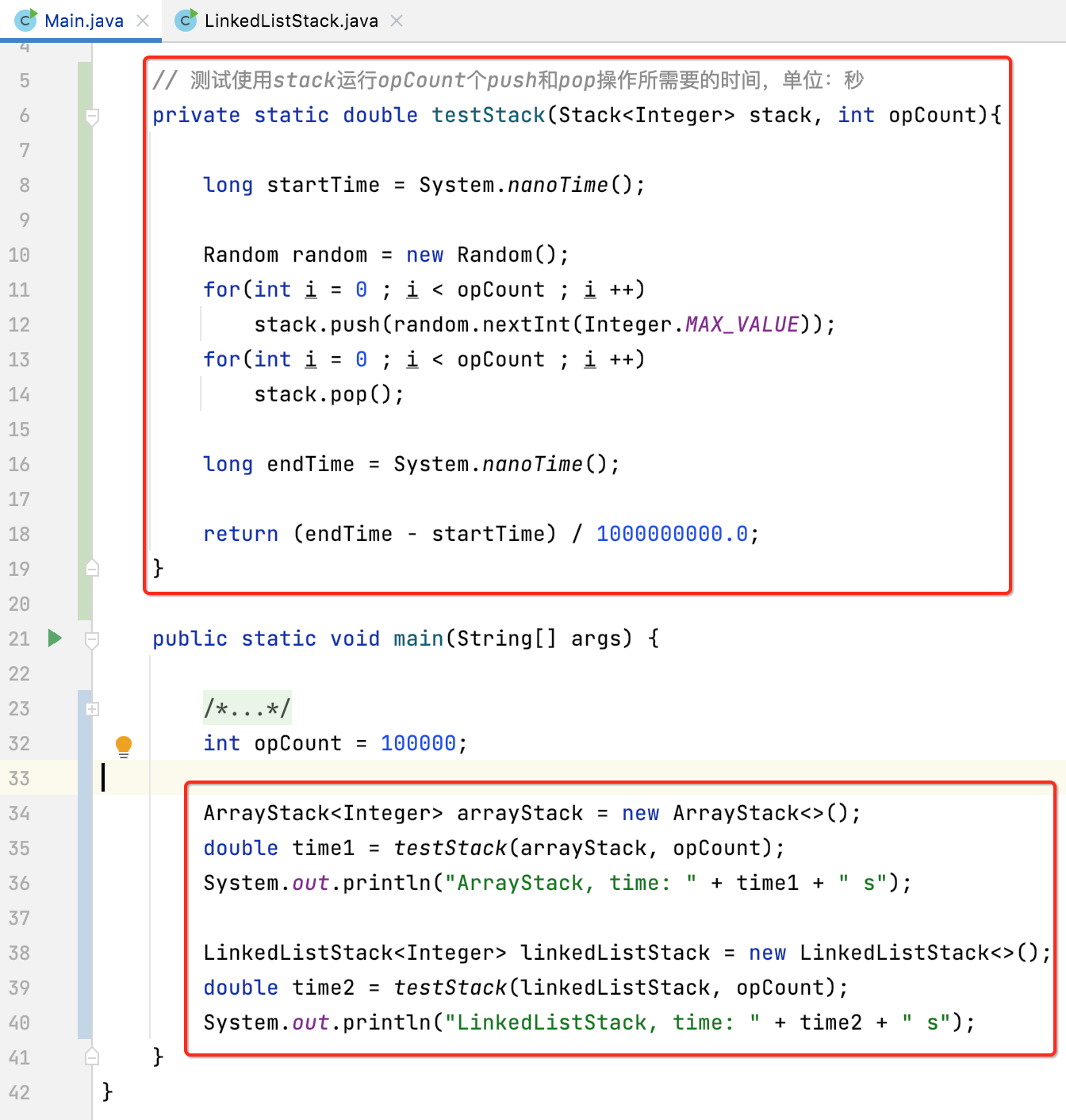
先用10万个数来测试一下,结果为:
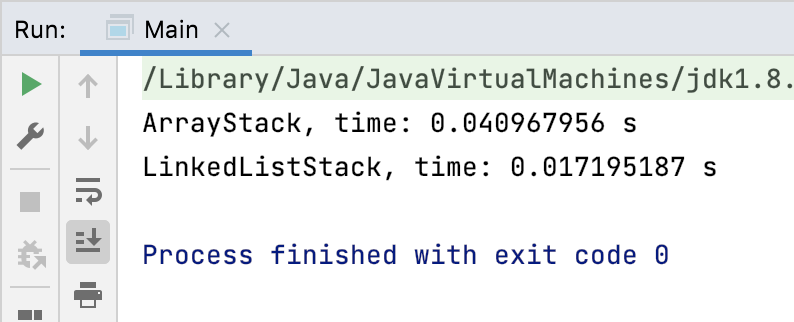
很明显,链表实现的栈的性能要比数组实现的栈要好对吧,这是因为数组实现的栈需要不断的重新申请静态数组,然后将原来数组的元素复制拷贝到新的数组中,这个过程是比较耗时的,而用链表实现的栈是不存在这个情况的,但是!!!这个结论不是一定的,下面咱们将测试数据由10万加到大1000万,再来看一下运行结果:
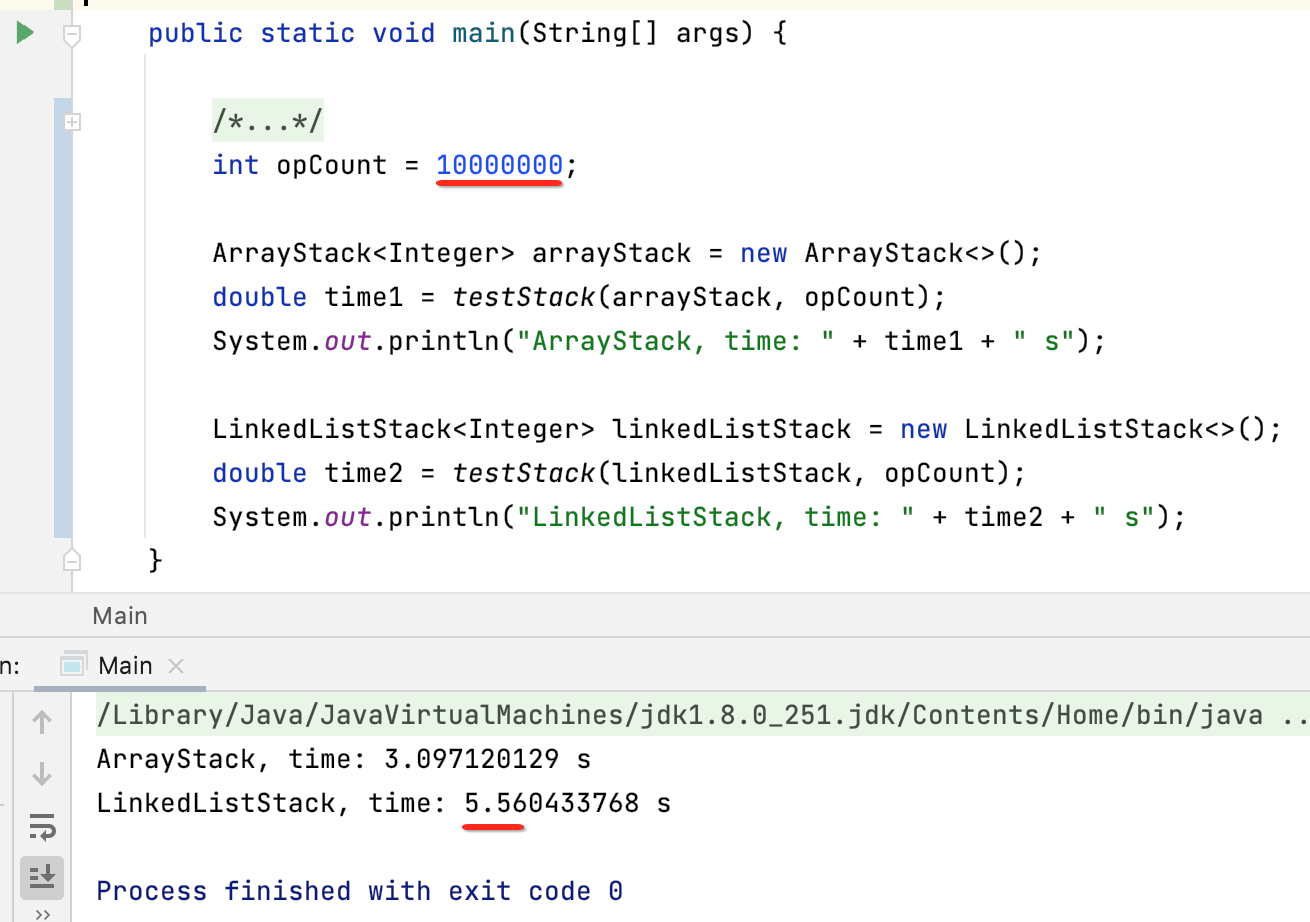
看到了么,居然比用数组实现的链表要慢好多,其实这个原因是由于LinkedListStack中的LinkedList里面会有很多的new Node的操作:
而new操作它是依赖于机器的操作系统、使用JVM的版本、操作数的多少,因为需要不断的开辟空间,这个是比较耗时的,那是不是可以给出一个结论:数组栈的性能要优于链表栈呢?不能!!!其实它们俩的性能差不多,也就是同一复杂度,因为它们之间并没有复杂度上“巨大”的差异,你看这个1000万次的测试出的结果两者其实也就相差2秒多对吧,并没有几百倍的差异对吧,而不像之前https://www.cnblogs.com/webor2006/p/14216904.html所测试的数组队列和循环队列之间的性能差异:
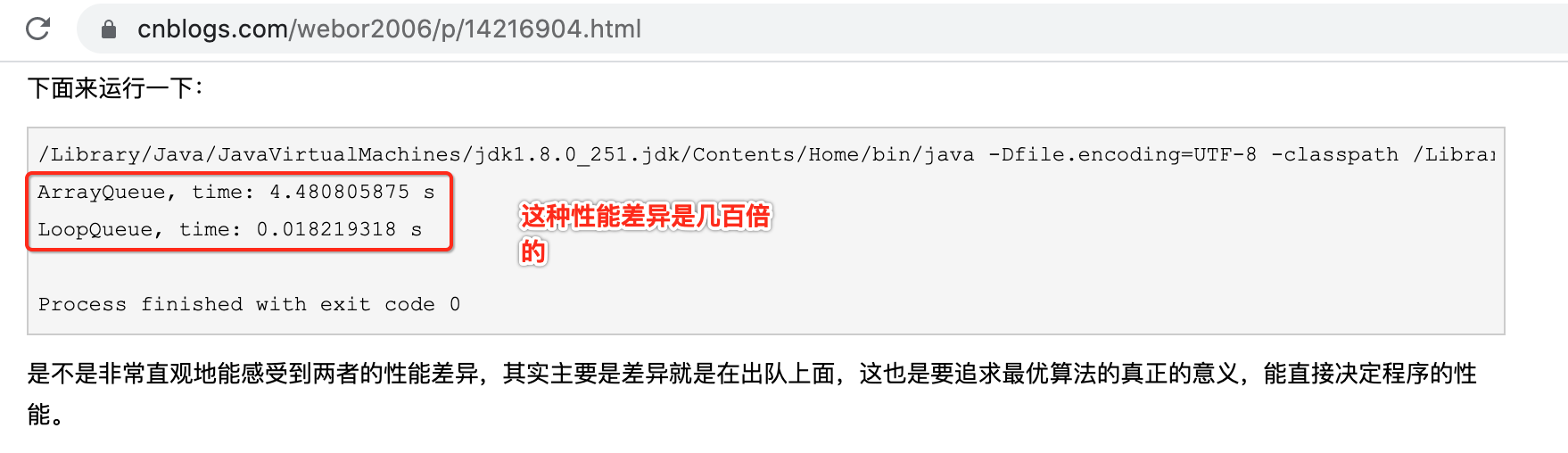
也就是说,咱们以后对于像链表栈和数组栈这之间的性能差异可以认为是同等级别的,重心关注点不在于这种小性能差异上,而应该是关注在数据结构底层原理的实现上,而真正能体现性能差异的就要以像数组队列和循环队列它们为例,有几百倍的,关于这一点需要明确一下。
数组队列和循环队列
带有尾指针的链表:使用链表实现队列:
前言:
目前咱们已经用自己实现的链表来实现了栈了,接下来则尝试用它来实现队列,在正式实现之前,还得从咱们链表的时间复杂度上来考虑一下目前要实现队列的困难:

其中增、删、查操作如果只对链表头进行操作复杂度都是O(1)级别的,而如果是从链表尾进行操作则就变成了O(n),回想一下队列这种数组结构:
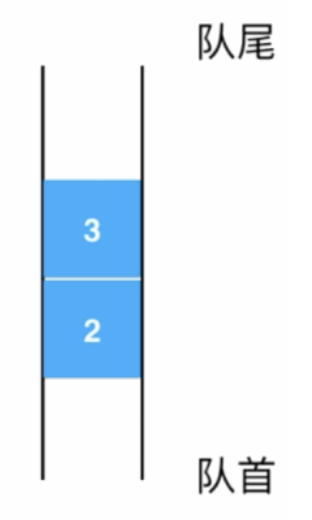
很明显会对线性结构的两端都要操作,那势必有一端的操作就是O(n)级别的,这肯定不是我们所期望的,毕竟O(n)级别的算法性能是比较差的,其实在之前https://www.cnblogs.com/webor2006/p/14216904.html学习使用数组实现队列也存在相同的问题:

为了改进,则引入了循环队列:

所以,同样的,如果想要用链表来实现队列,在实现之前也得先来改进咱们的链表才行。
改进链表:
改进思路:
那如何改进咱们的链表呢?对于目前咱们的链表是这样的一个结构:
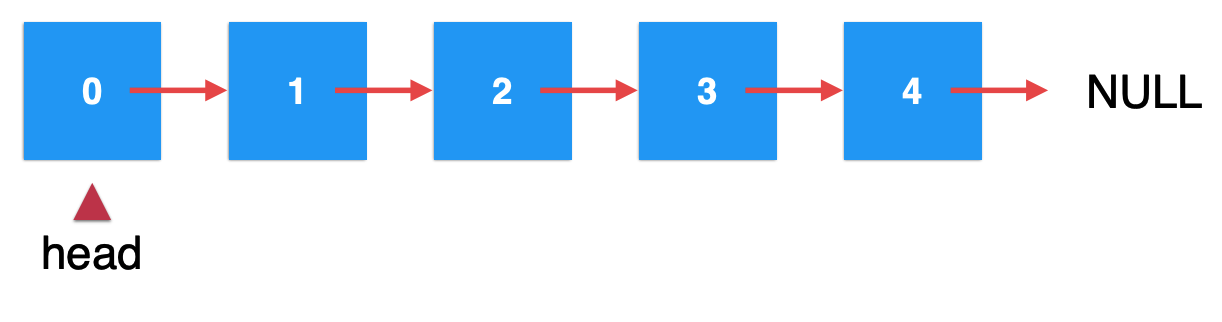
其在链表头部的所有操作复杂度都是O(n)的原因在于有一个head指针指向头结点对吧,那现在咱们想改进在链表的尾部插入复杂度过高的问题,其解决思路也很顺其自然地能想到,也就是再用一个指针用来指向链表的尾部在哪:
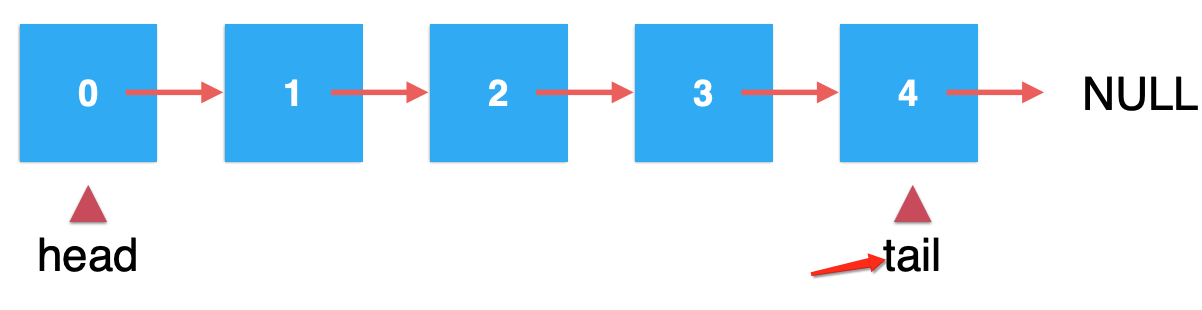
那可以看到,如果有了这个尾部的tail之后,从两端插入和查找元素是不是都成了O(1)的了?也就是目前这样一改造对于这俩的复杂度问题就可以解决了:
其中还剩一个“删”操作对吧,其实对于目前的改进来说“删”操作还是性能不好的,因为对于一个链表的删除操作来说,需要找到待删除元素的前一个元素才行,但是!!!看一下咱们目前链表的结构:
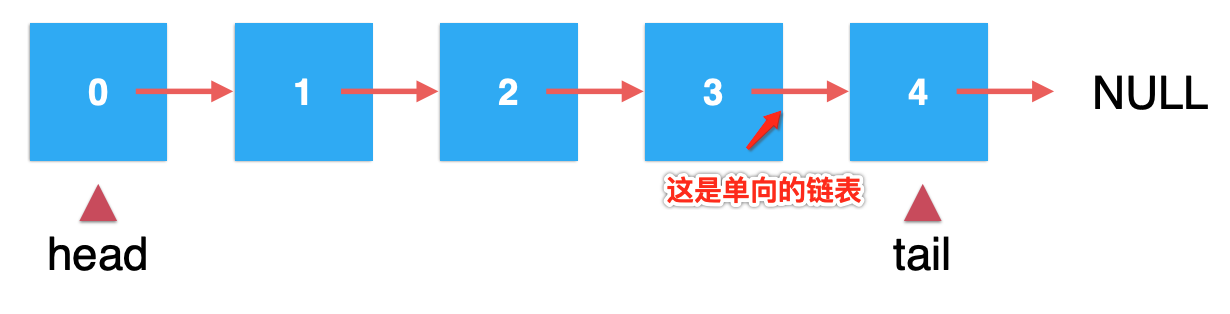
那改成循环链表就不行了,是可以,只是目前暂不弄这么复杂,只是基于单向链表的基础来进行实现,所以目前的这种改进是改善不了从尾部删除元素的复杂度的,依然需要从头进行遍历从而来找到tail结点的前一个结点进行元素的删除,但是!!!这种改进足以满足目前要用它来实现队列的需求了,为什么呢?咱们来挼一下,目前这种改进的链表我们可以按这个原则来使用呀: 从head端删除元素,从tail端插入元素,那对于head和tail哪一个可以作为队列的队首和队尾呢?很明显:
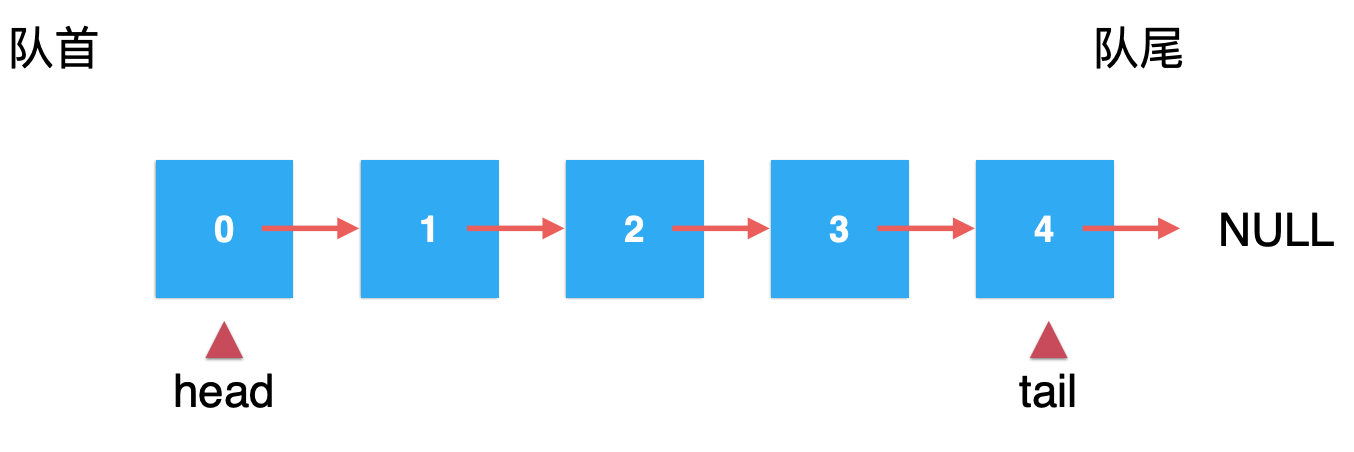
head作为队首,tail作为队尾,此时你可能会有点懵,原因还是在于“一定”要对队列的队首和队尾的角度要清晰的明白,队首是用来出队的,也就是一个“删除”的动作,而队尾是用来入队的,也就是一个“插入”的动作,如果还是有点晕,记得回看一下这个图:

所以,这样一分析,只要将咱们的链表增加一个tail引用就好了。
另外,还有一个细节需要提前说明一下,就是在使用链表实现栈时,我使用的链表是一个带虚拟头结点的版本:

而由于这次使用链表来实现的队列的操作都是在链表的两端(head、tail)完成,不存在中间元素和两侧元素操作逻辑不统一的问题(关于逻辑不一统的原因这里就不过多说明了,之前https://www.cnblogs.com/webor2006/p/15319904.html详细说过了,可以回头复习一下), 所以这次就不使用带虚拟头结点的链表了,而正因为没有了虚拟头结点了,所以在实现时需要注意当链表为空时其head和tail都指向空的这种特殊情况。好,整体改造的思路已经挼清楚了,接下来则就正式开始实现。
改进实践:
1、新建LinkedListQueue:
这里还是打开原来学习队列的工程:
在这里面进行实现,新建一个类:
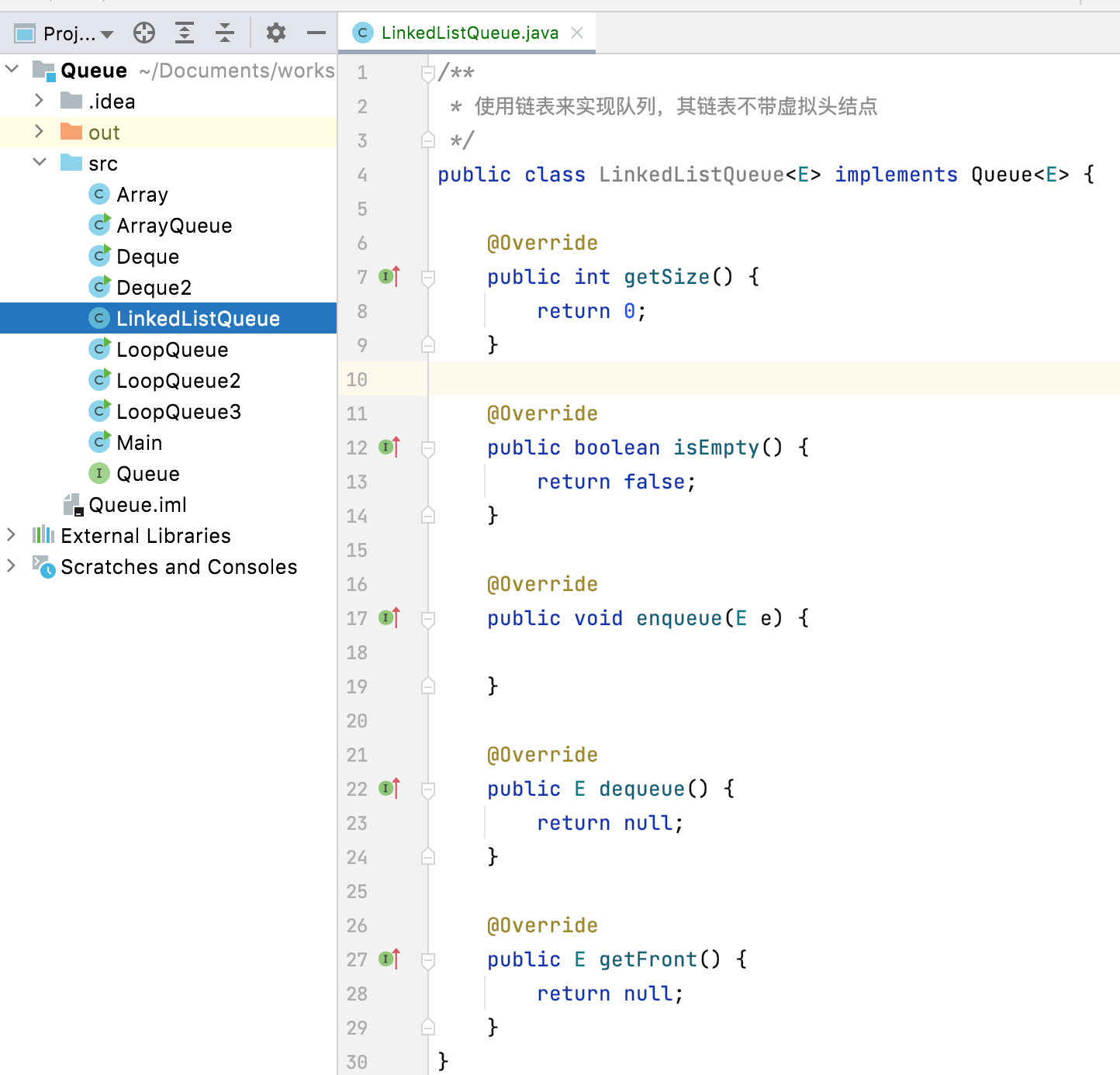
注意:此时就不像上面使用链表实现栈一样,copy之前咱们已经实现好的链表进工程了:
因为这个版本没有尾指针嘛,这里打算直接在LinkedListQueue类中进行链表结构的构造。
2、定义Node:
既然要重新定义链表结构,首先得定义Node结点对吧,直接将之前链表实现中的Node拷进来:
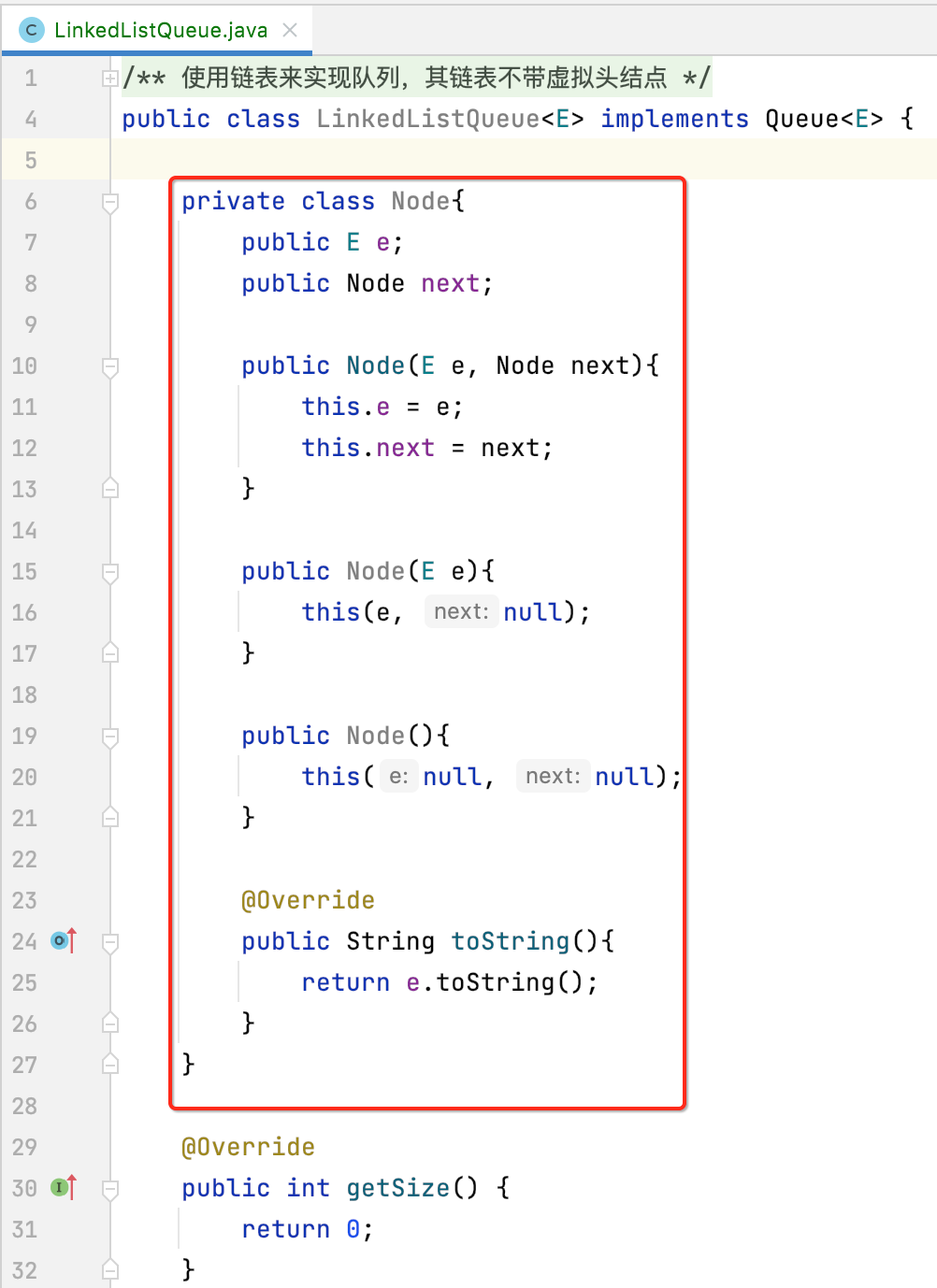
3、定义成员变量:
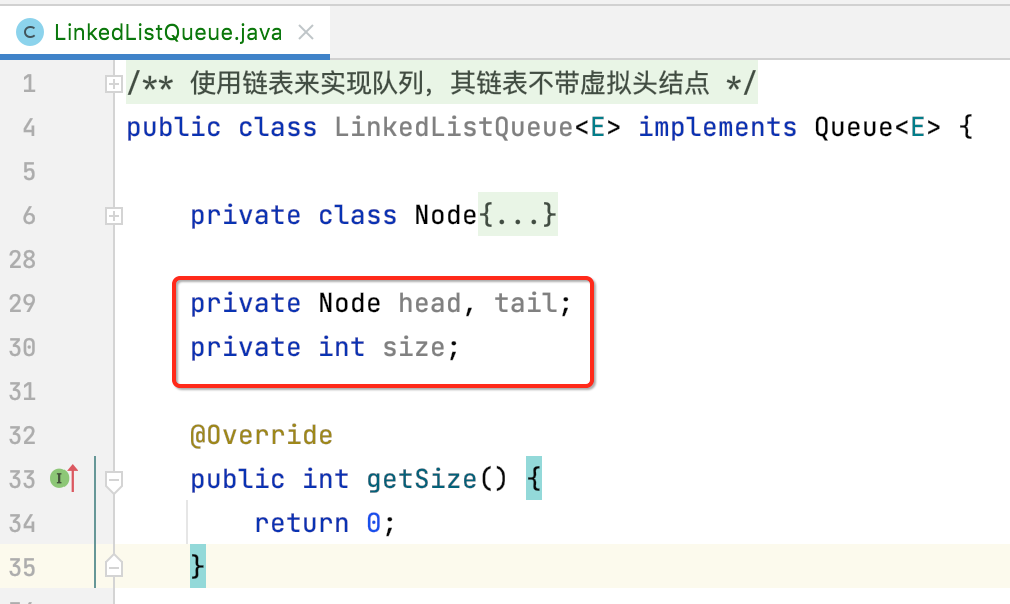
其中相比之前链表实现,就是多了一个tail结点。
4、getSize()、isEmpty():
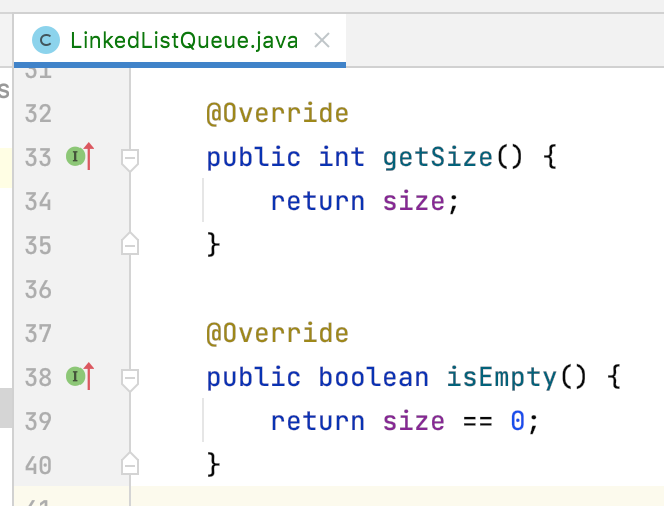
5、enqueue():
根据咱们上面所分析的,按照“队首是用来出队的,队尾是用来入队的”的原则,这里入队需要从队尾来进行,也就是:
首先判断head是否为null,如果它为null,肯定tail也为null,因为说明里面还没有元素,所以先来处理这种条件:

接下来的条件则是将元素从尾部插入,如下:
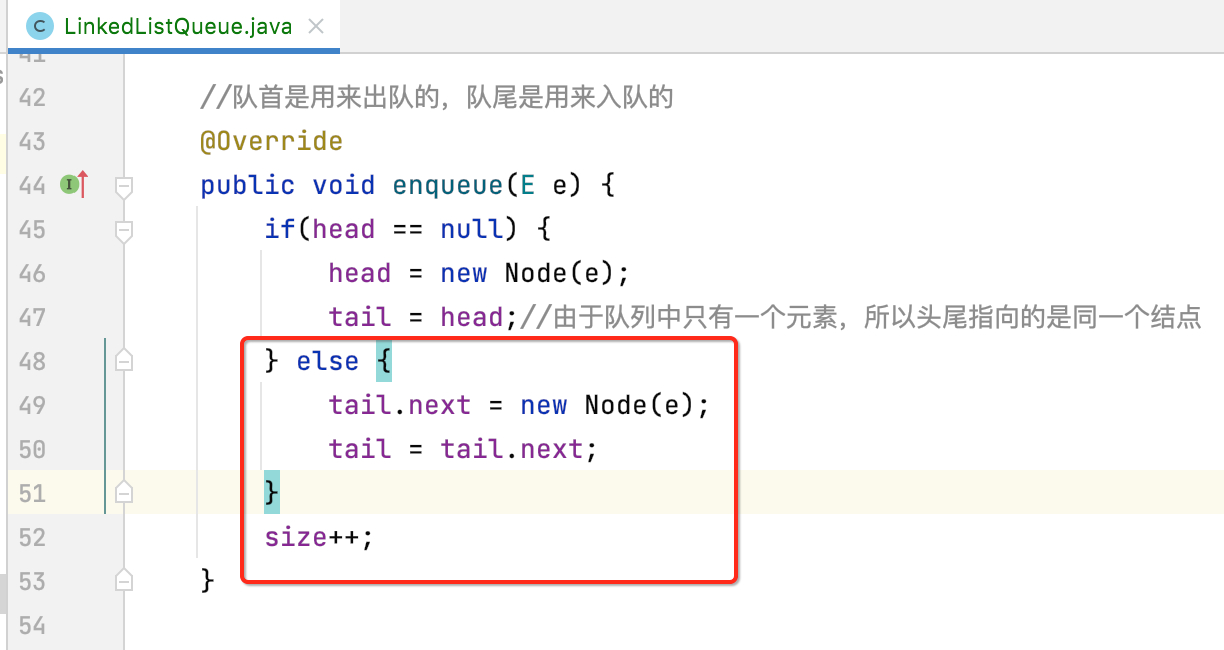
6、dequeue():
出队是从队首,首先需要判空:

然后直接从head结点取:

最后需要处理一种情况,就是head为null的情况:

7、剩余的操作:

8、测试:
接下来再来测试一下咱们所编写的队列,看逻辑是否有问题,其测试用例完全按照之前咱们所实现的队列测试一样:
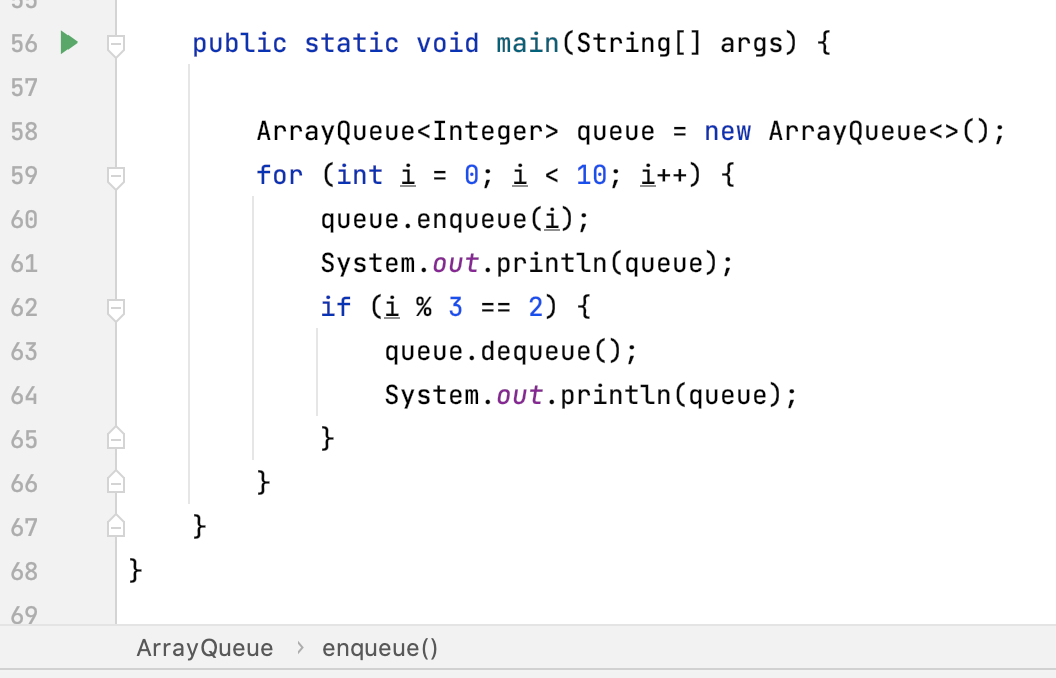
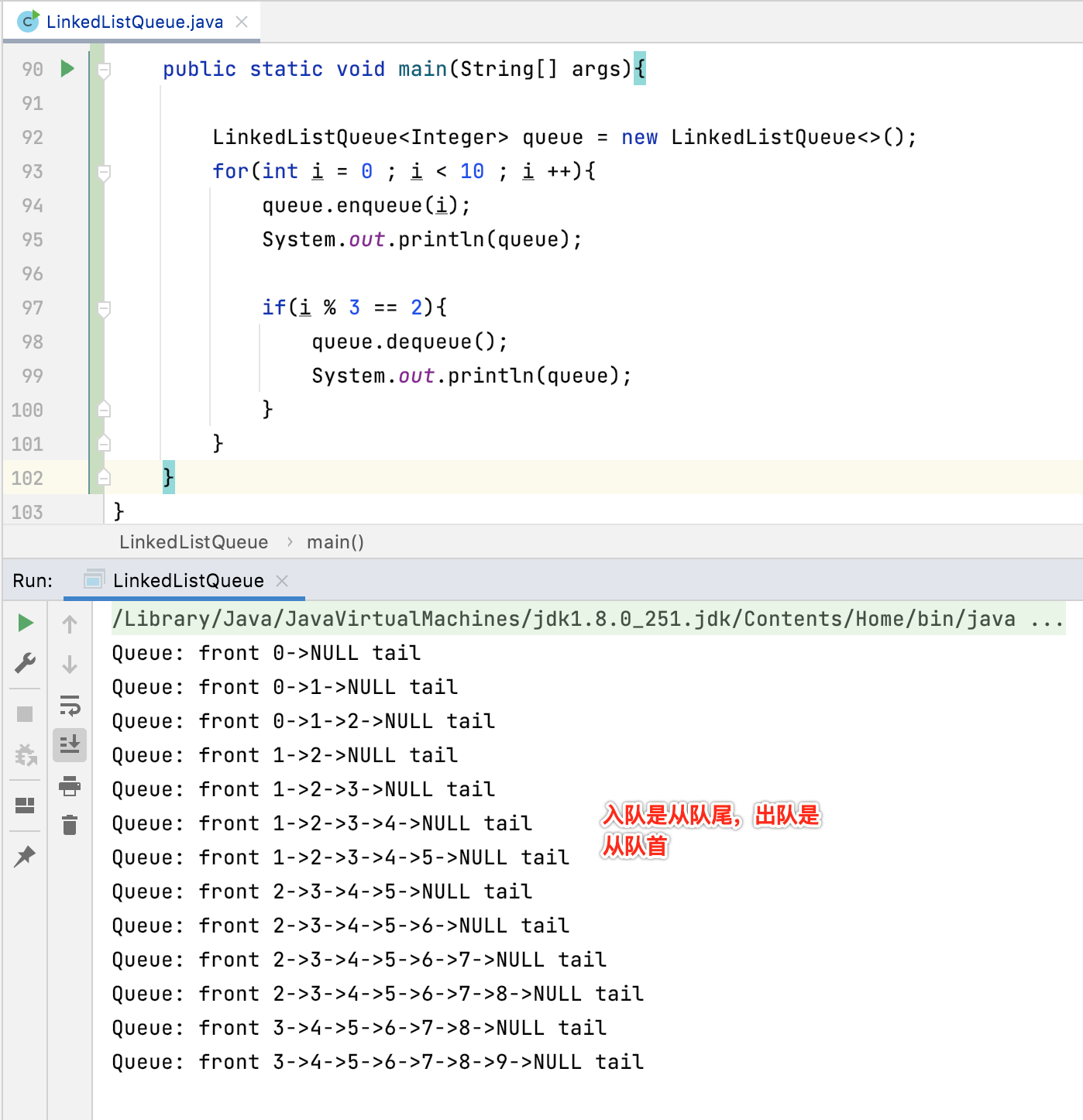
9、性能对比:
在之前咱们对这两个已实现的队列进行了一个性能对比:
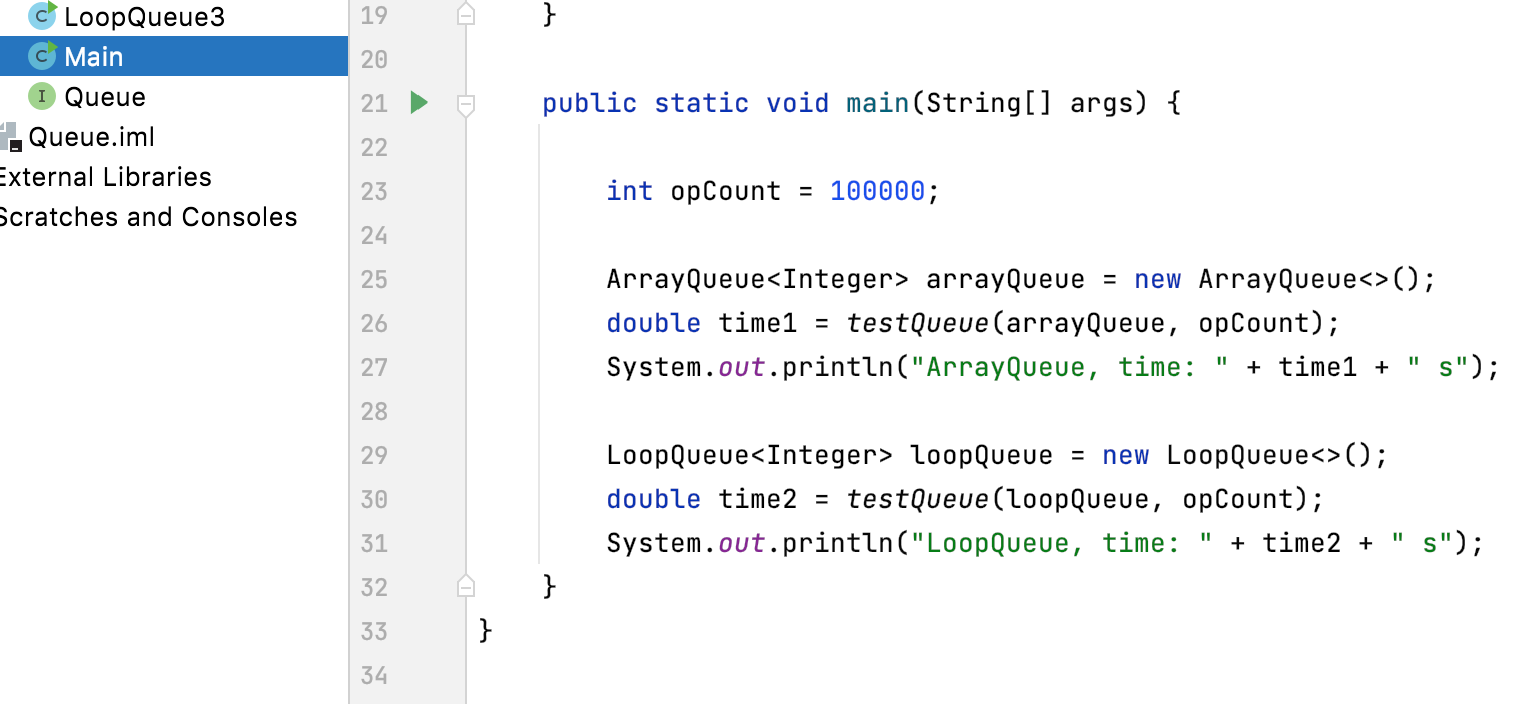
同样,咱们把这次实现的带尾结点的队列也加入性能测试对比中看一下:
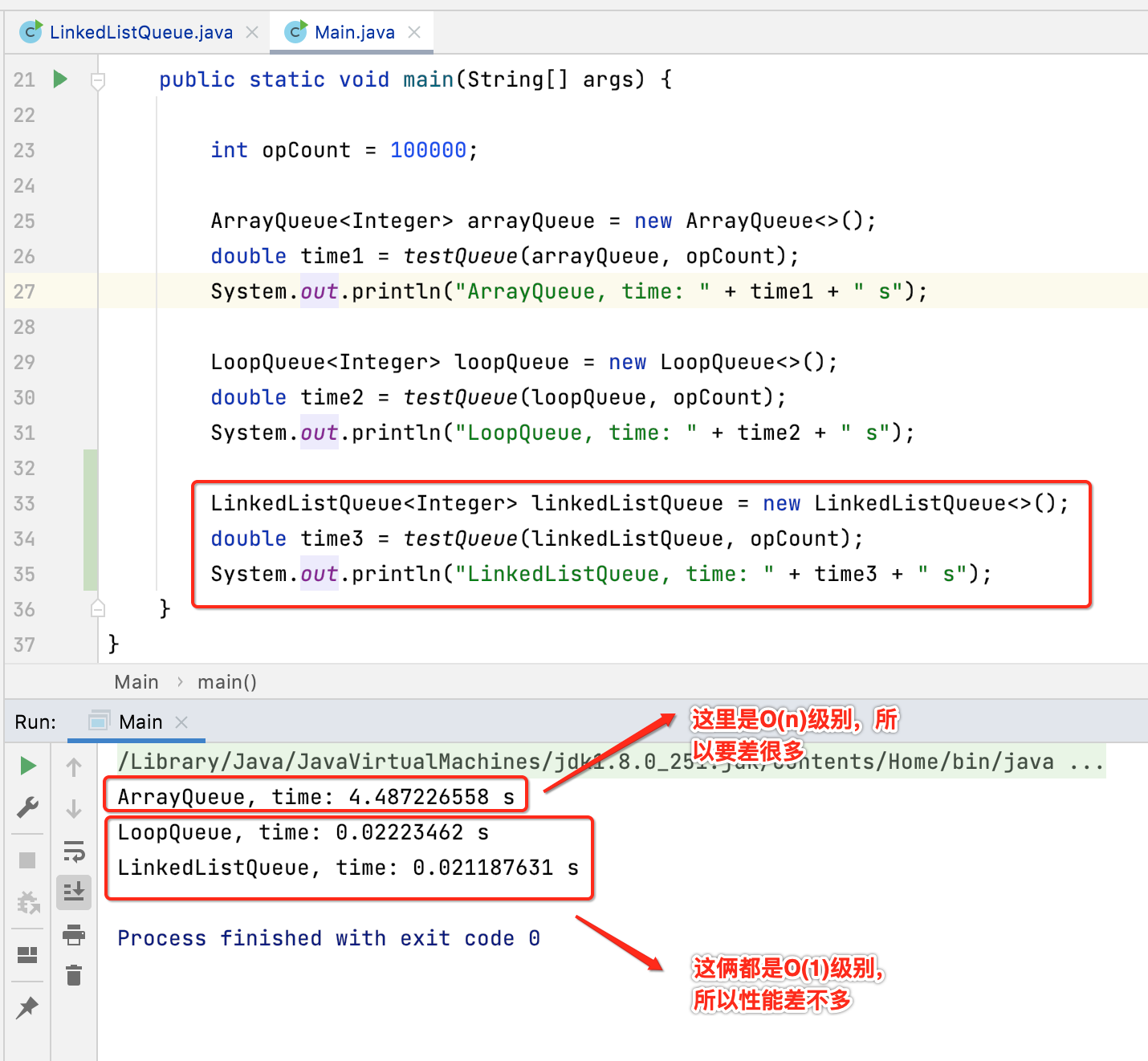
链表的性能问题:
概述:
接下来探讨一下性能的话题,也是比较容易误解的话题,就是对于咱们实现的链表,如果只在链表头中添加元素,其时间复杂度是O(1)对吧:
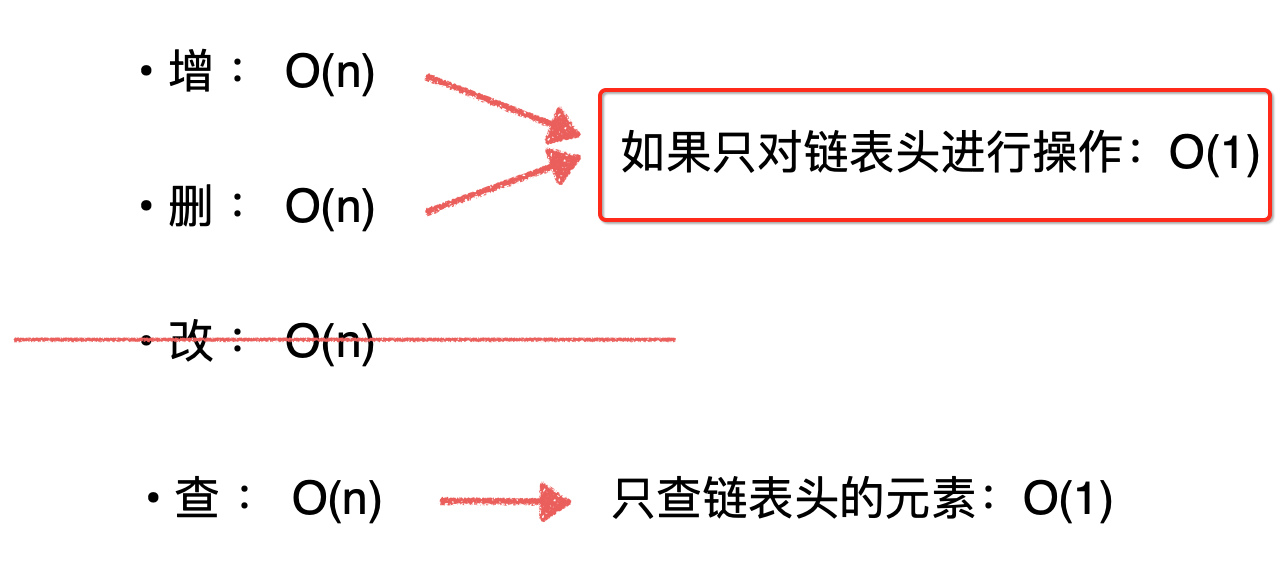
因为链表不需要像数组那样需要resize,性能应该是非常好的,而对于咱们之前https://www.cnblogs.com/webor2006/p/14092866.html实现的Array往尾部添加元素的复杂度也是O(1)对吧,那它们俩是不是性能都一模一样呢?实际上,当数据量达到一定程度,链表的性能相比动态数组而言是更差的,这是因为,对于链表来说,每添加一个元素,都需要重新创建一个 Node 类的对象,也就是都需要 进行一次 new 的内存操作。而对内存的操作,是非常慢的。 那你说慢就慢呀,有啥证据,下面用实验来验证一下。
验证:
下面回到链表的工程中,将咱们之前所实现的Array类拷进来:
然后用这么一个测试用例来测试一下:
//比较LinkedList和Array添加元素的性能 public static void main(String[] args) { // 创建一个动态数组,再创建一个链表 Array array = new Array<>(); LinkedList list = new LinkedList<>(); // 对于 1000 万规模的数据 int n = 10000000; System.out.println("n = " + n); // 计时,看将 1000 万个元素放入数组中,时间是多少 long startTime = System.nanoTime(); // 对于数组,我们使用 addLast,每一次操作时间复杂度都是 O(1) 的 for(int i = 0; i < n; i ++) array.addLast(i); long endTime = System.nanoTime(); double time = (endTime - startTime) / 1000000000.0; System.out.println("Array : " + time + " s"); // 计时,看将 1000 万个元素放入链表中,时间是多少 startTime = System.nanoTime(); // 对于链表,我们使用 addFirst,每一次操作时间复杂度都是 O(1) 的 for(int i = 0; i < n; i ++) list.addFirst(i); endTime = System.nanoTime(); time = (endTime - startTime) / 1000000000.0;
System.out.println("LinkedList : " + time + " s"); }
运行:
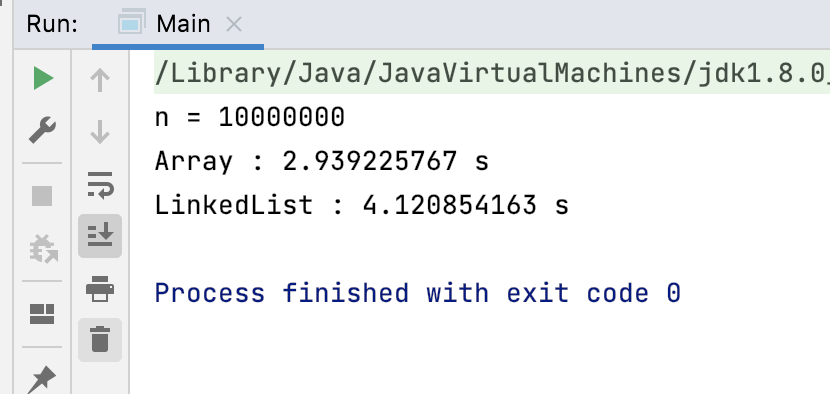
看到木有,是不是链表明显要慢于动态数组?
那为什么即使有 resize,对于大规模数据,动态数组还是会快于链表?这是因为对于动态数组来说,一方面,每次 resize 容量增倍,这将使得,对于大规模数据,实际上触发 resize 的次数是非常少的。更重要的是,resize 的过程,是一次申请一大片内存空间。但是对于链表来说,每次只是申请一个 空间。申请一次 10 万的空间,是远远快于申请 10 万次 1 的空间的。而相较于堆内存空间的操作,动态数组的 resize 过程虽然还需要赋值,把旧数组的元素拷贝给新数组。但是这个拷贝过程,是远远快于对内存的操作的。
关于这个细节需要了解一下,虽说都是O(1)时间复杂度的,但是在大规模数据的情况下还是有性能差异的。
链表与递归:
前言:
对于链表这个数据结构而言,还有一个非常重要与之相关的话题,那就是递归, 可能在数据结构中通常递归是与树进行挂勾的,确实是如此,树这种结构使用递归也是非常自然的,但是对于链表这个数据结构其实也是可以使用递归的,这是因为链表天然就具备有递归的性质,只不过由于链表太简单了,它是一个线性的结构,我们用非递归的方式也很容易解决链表上的问题而已,而从链表就开始打好递归的基础对于后续更加深入的学习“树”这种数据结构包括更加深刻的理解递归算法都是非常有好处的。
从Leetcode上一个问题开始:
概述:
这里会以一个Leetcode上的题目为话题进行链表相关问题的探讨,而不是还是利用自己实现的底层链表结构,这是因为在Leetcode上关于链表的题解是有一些注意的地方的,同时它跟我们自己写链表来解决问题的思路也是有一些不同的,这里来看Leetcode上的这个问题:https://leetcode-cn.com/problems/remove-linked-list-elements/
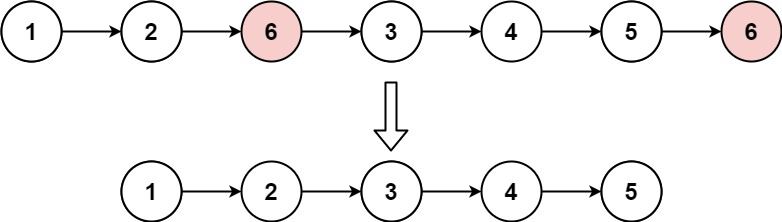
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
示例 1:
输入:head = [1,2,6,3,4,5,6], val = 6 输出:[1,2,3,4,5]示例 2:
输入:head = [], val = 1 输出:[]示例 3:
输入:head = [7,7,7,7], val = 7 输出:[]提示:
列表中的节点数目在范围 [0, 104] 内
1 <= Node.val <= 50
0 <= val <= 50来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/remove-linked-list-elements
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题目要求也比较容易理解,就不过多说明了,其中,看到它给的解题代码模板如下:
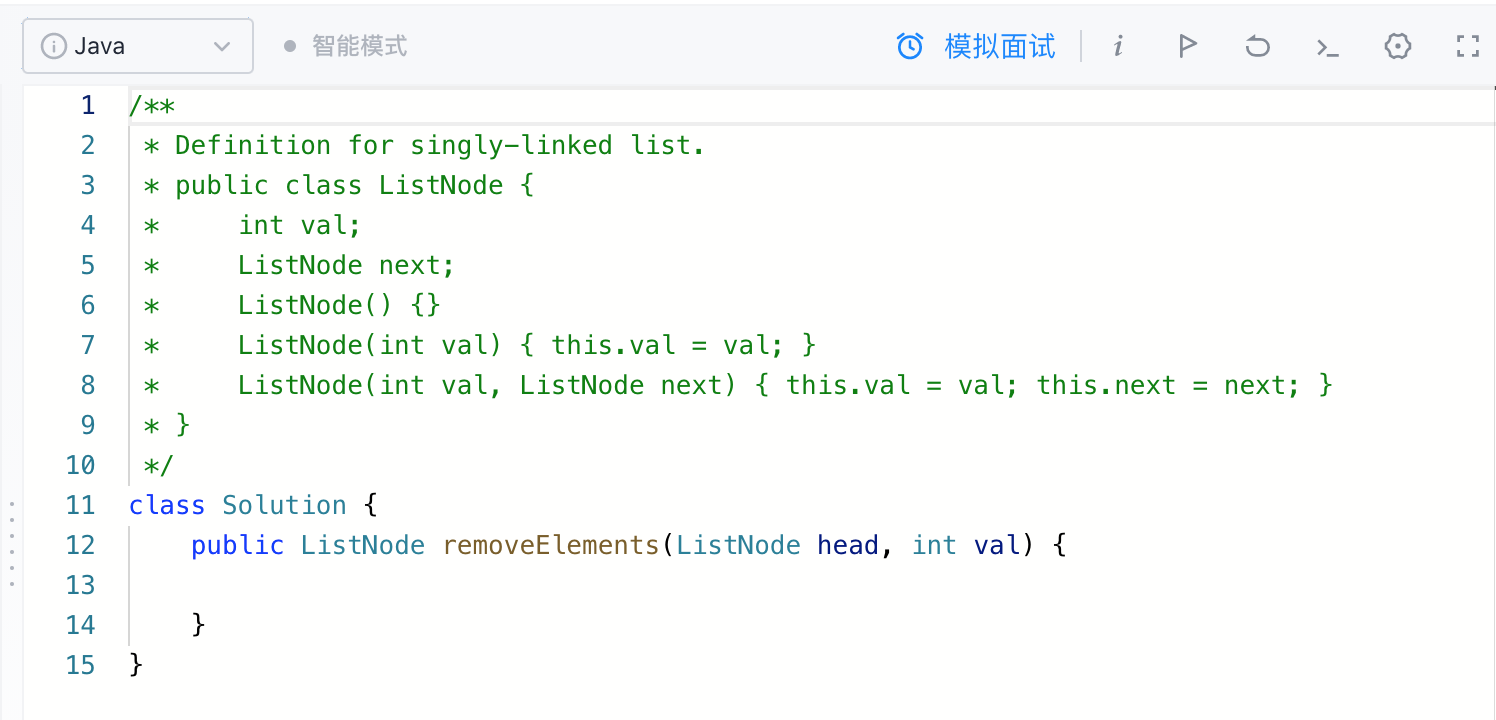
这里跟咱们之前所学习的LeetCode题目不同的一点是,这里需要借助是Leetcode为咱们已经准备好的ListNode类,也就是注释说明上所说明的:
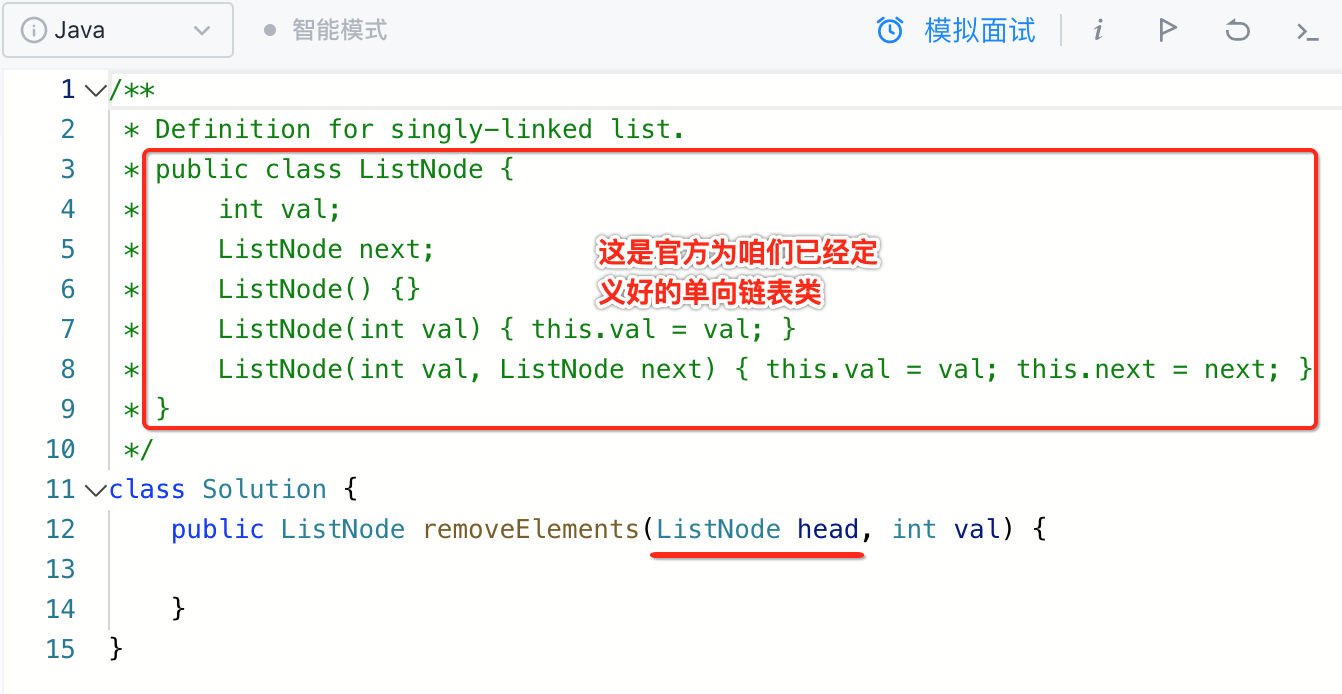
这里要注意了,这里的ListNode类咱们是不能自己来创建的哟,只能使用官方给出的这个结构的ListNode类。
解题:
1、将LeetCode提供的模板代码拷至工程:
新建一个工程,然后将LeetCode的模板代码拷进来:

此时缺一个ListNode类对吧,这里新建一个,然后用LeetCode提供ListNode的内容填充既可:
这样,当我们代码编写完之后,只需要提交Solution这个类到LeetCode上既可。
2、思考:
接下来则来编写具体的删除逻辑,这里简单想一下,其实可以有两个版本,一个是带虚拟头结点,一个是不带虚拟头结点,因为在当时我们自己实现链表时就已经实现过了,
这里打算将两个版本都实现一下,进一步来体会使用虚拟头结点之后给咱写逻辑带来的好处,也同时是一个复习+巩固。
3、实践:不使用虚拟头结点:
a、先处理head就是val的情况:
这个逻辑比较简单,如下:
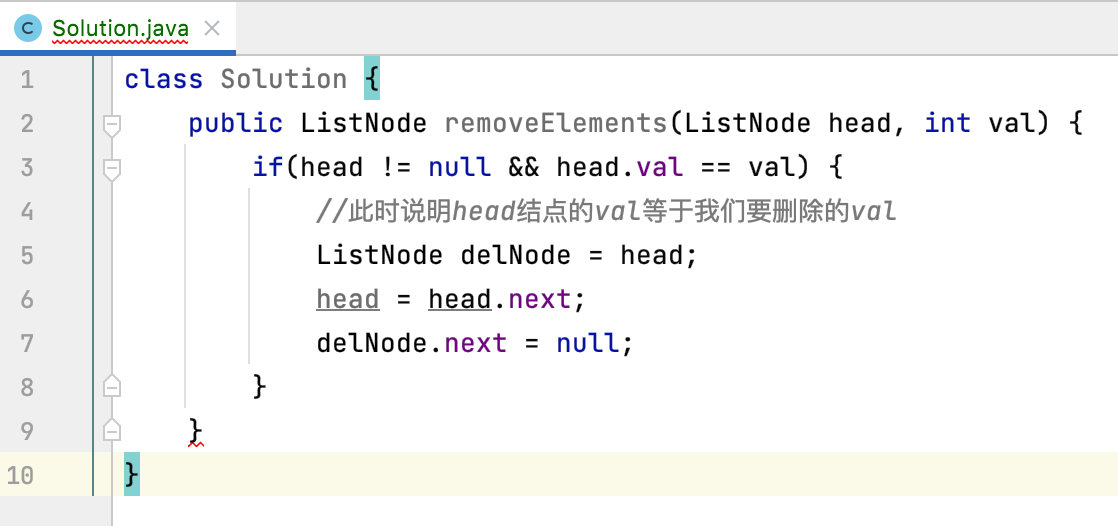
但是!!!那如果接下来这个头接点又等于我们要删除的val呢?所以,这里应该是一个循环才对对吧:
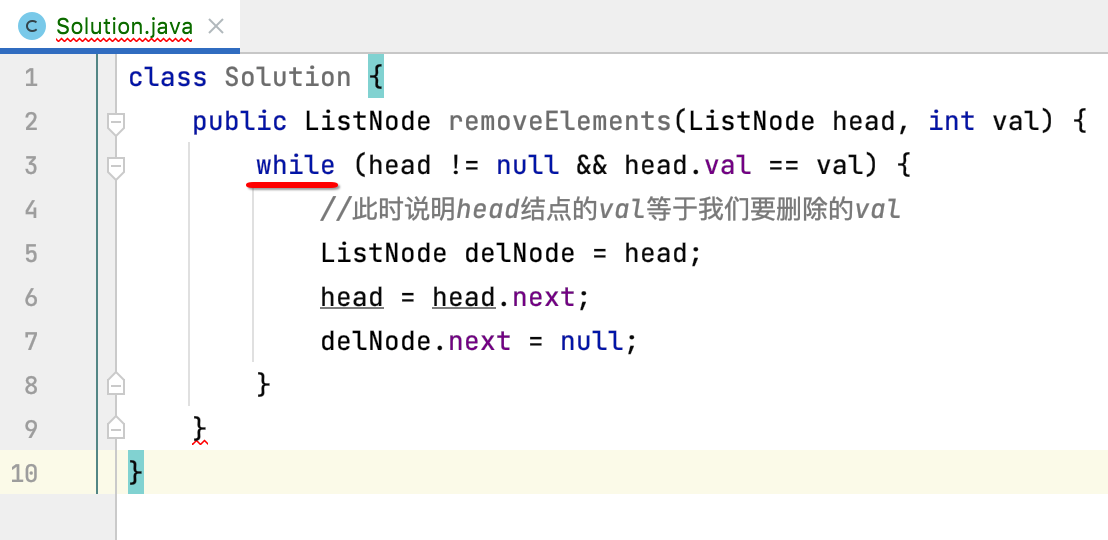
接着,如果经过这么一层循环,发现所有的结点都是需要删除的,那么是不是head结点就为空了,此时直接返回就可以了,如下:
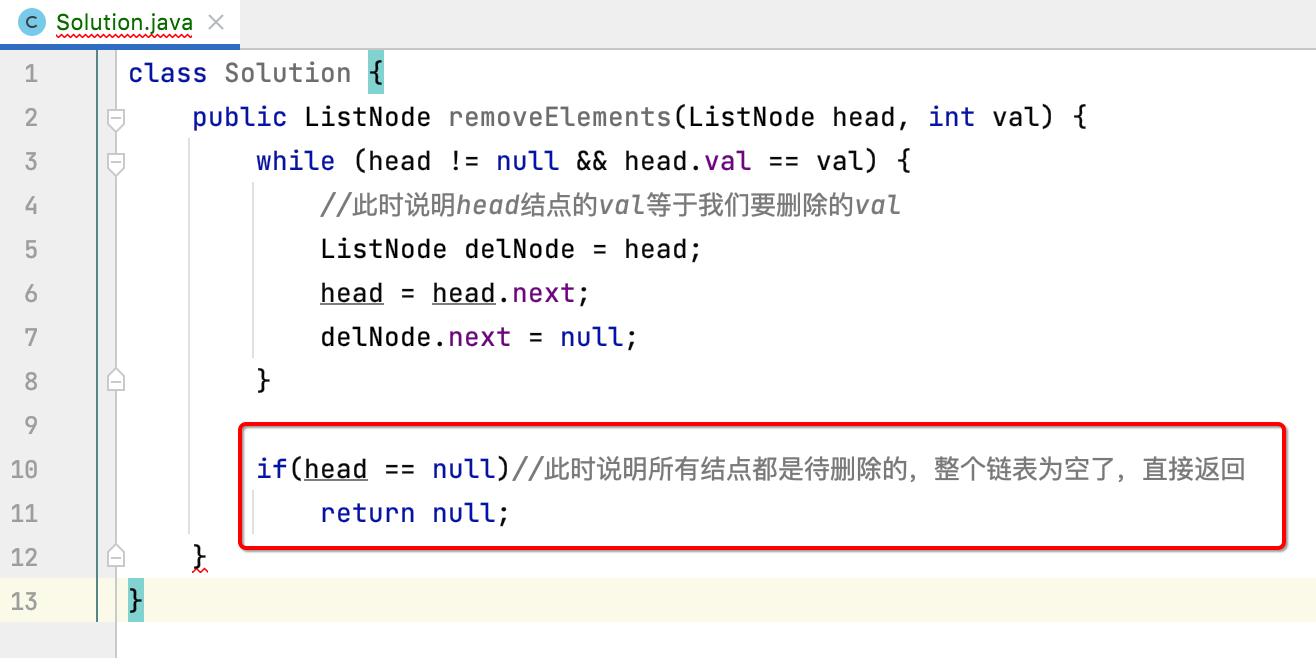
b、处理链表中间结点的删除逻辑:
其思路也很简单,在之前链表的编写中也已经写过一遍了,只需要找到待删除的上一个结点既可,这里直接贴出代码了:
//实现方式一:不使用虚拟头结点 class Solution { public ListNode removeElements(ListNode head, int val) { while (head != null && head.val == val) { //此时说明head结点的val等于我们要删除的val ListNode delNode = head; head = head.next; delNode.next = null; } if(head == null)//此时说明所有结点都是待删除的,整个链表为空了,直接返回 return null; ListNode prev = head; while(prev.next != null){ if(prev.next.val == val) { ListNode delNode = prev.next; prev.next = delNode.next; delNode.next = null; } else prev = prev.next; } return head; } }
c、提交至LeetCode验证:
接下来咱们将这个代码提交到LeetCode上验证一下逻辑是否正确:
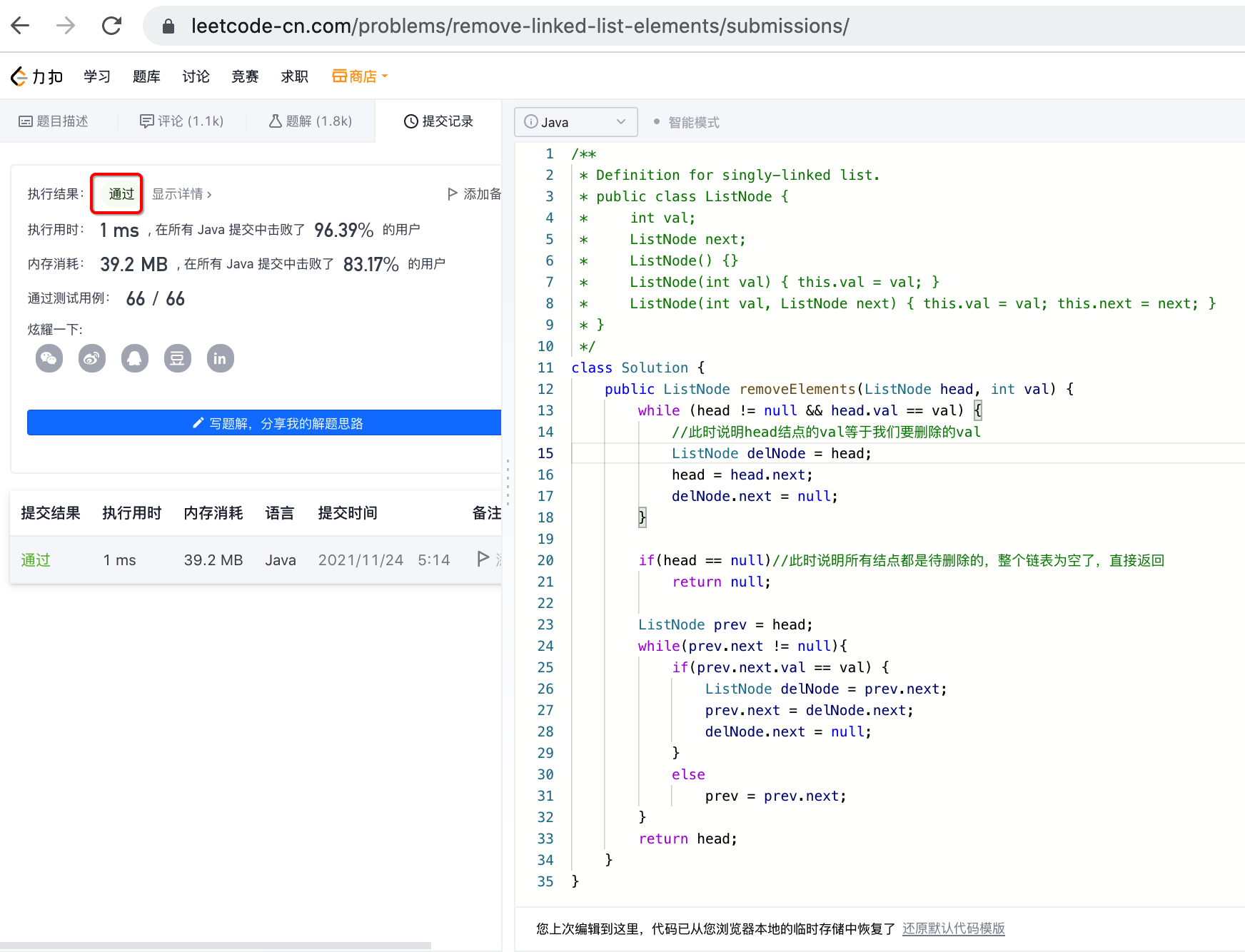
d、精简代码:
对于LeetCode来说,对于这些代码是可以一定程度的简化:
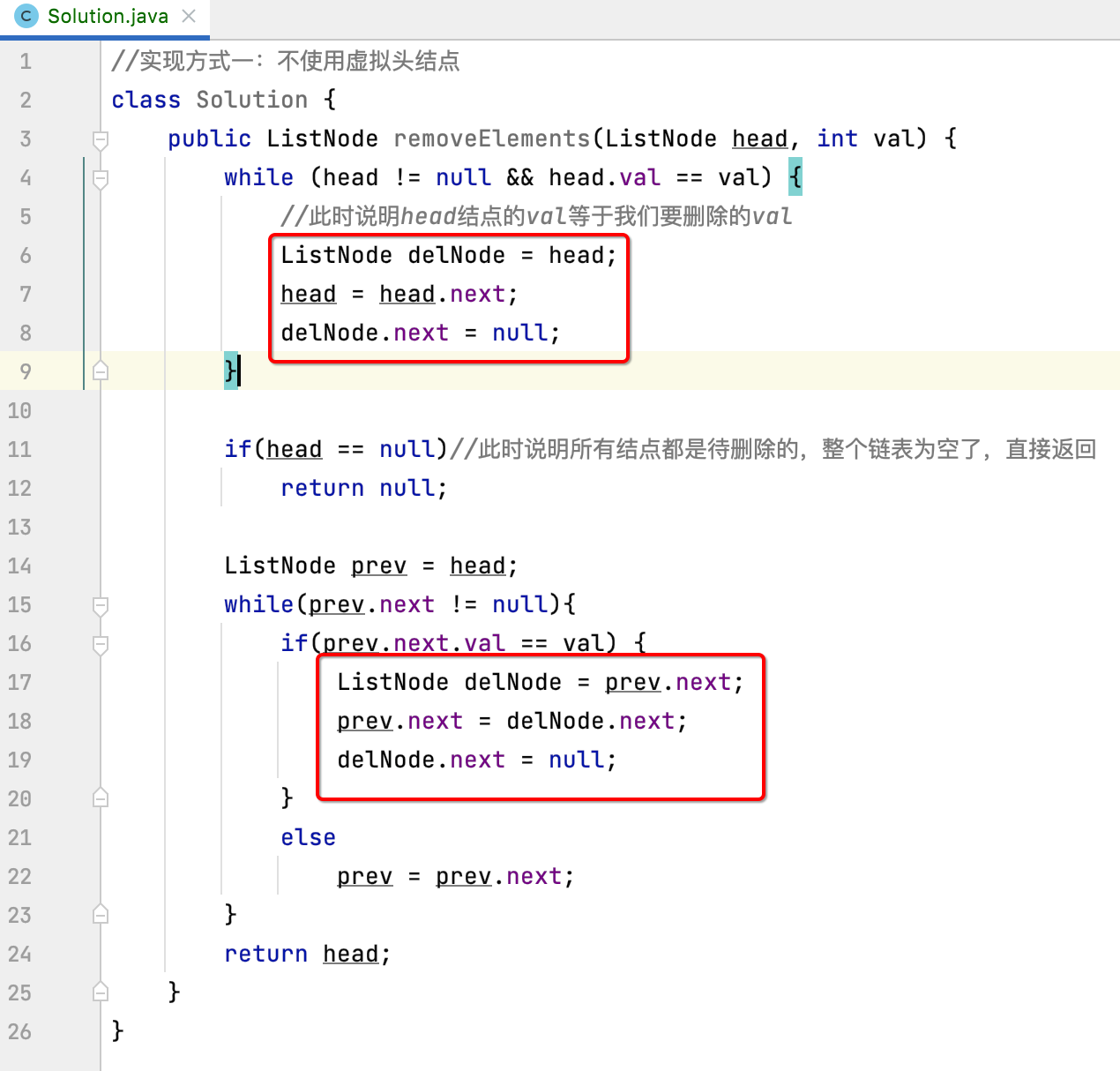
我们是考虑到了删除结点回收的逻辑对吧,其实在LeetCode中主要是运行这个算法, 不用太多过于纠结这些需要待回收的对象【这些对象专业术语叫“loitering objects”,关于这块可以参考https://www.cnblogs.com/webor2006/p/14092866.html】,因为这个程序在LeetCode执行完之后,所有的内存都会被销毁的,所以对于这两块代码就可以精简成:

再提交看一下:
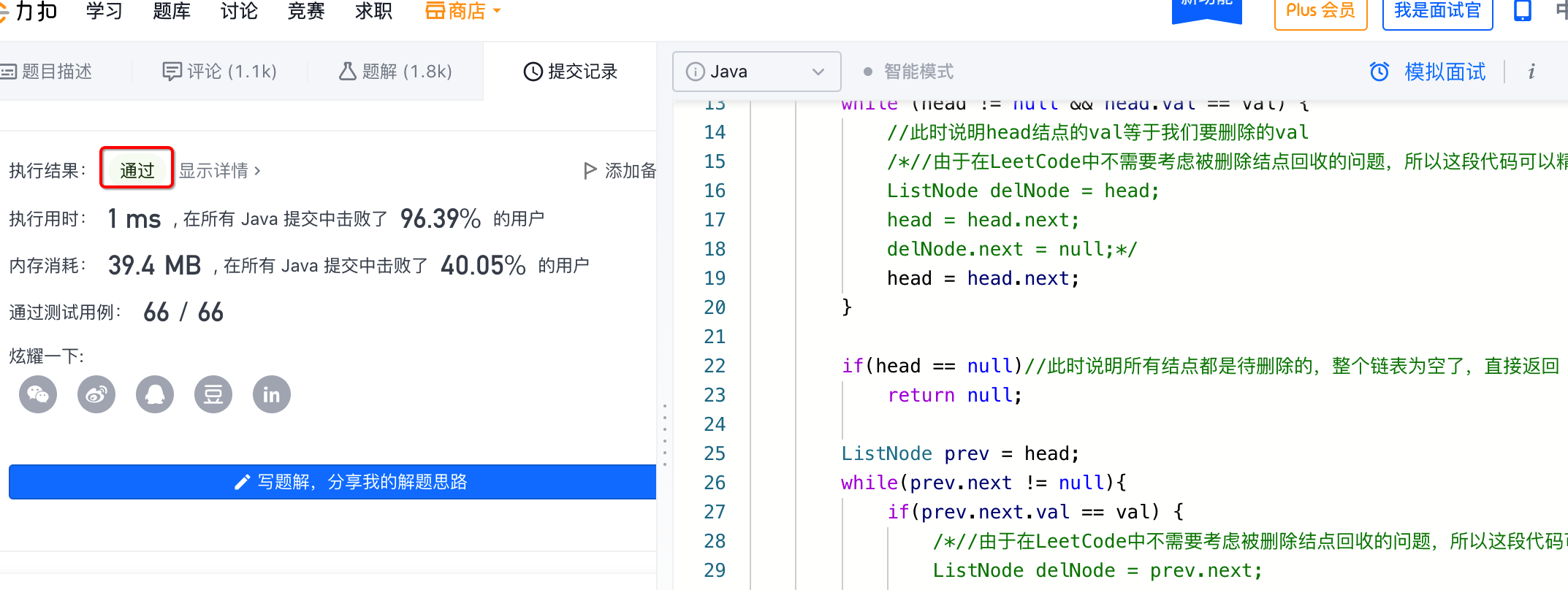
4、实践:使用虚拟头结点:
接下来再使用虚拟头结点的方式来实现一下,来体会使用虚拟头结点之后的好处,这里基于我们已经实现的不使用虚拟头结点的代码进行改造既可:
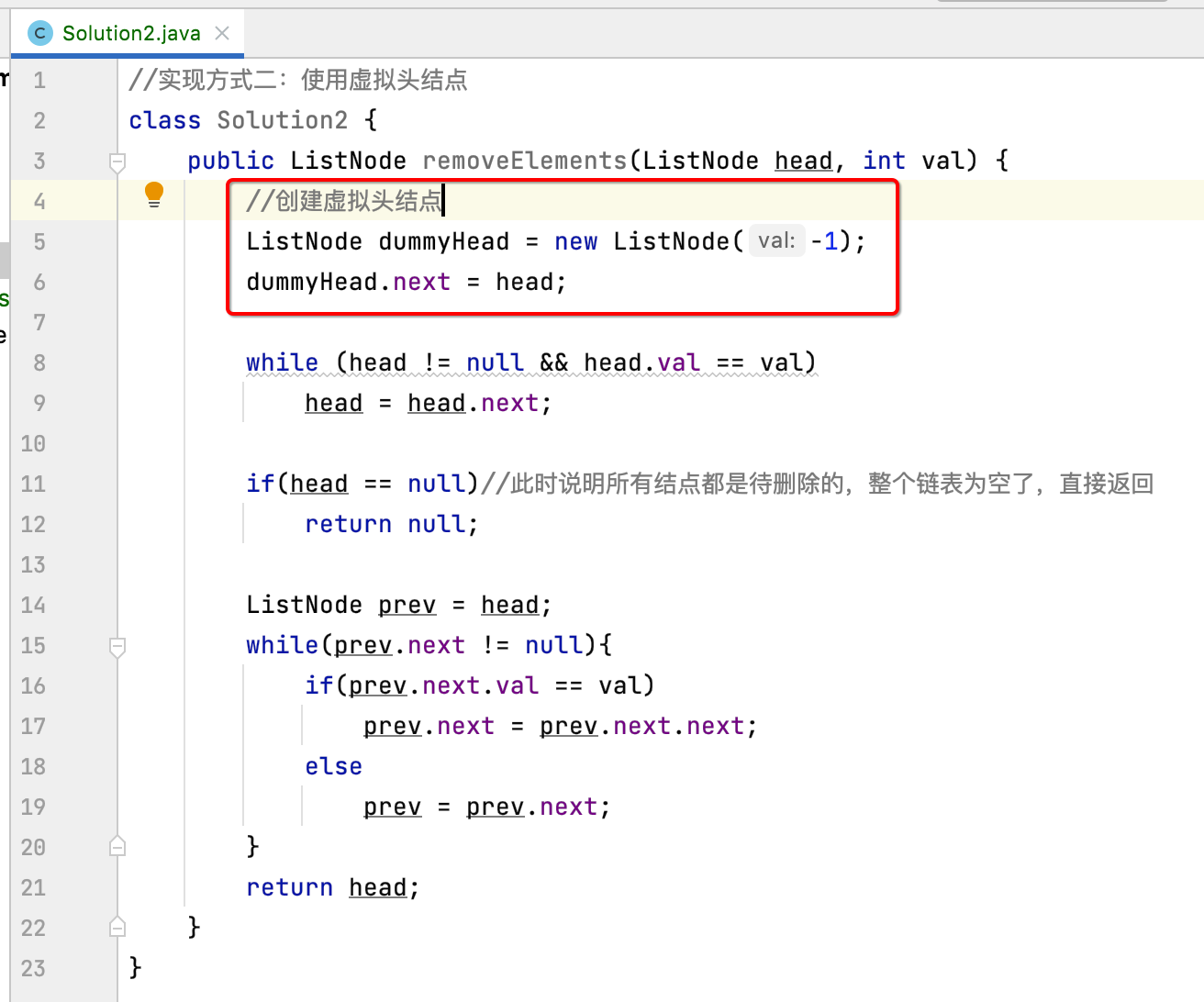
好,由于我们链表中的每一个元素都有前一个结点了对吧,所以此时这段特殊处理的逻辑就可以完全去掉了:
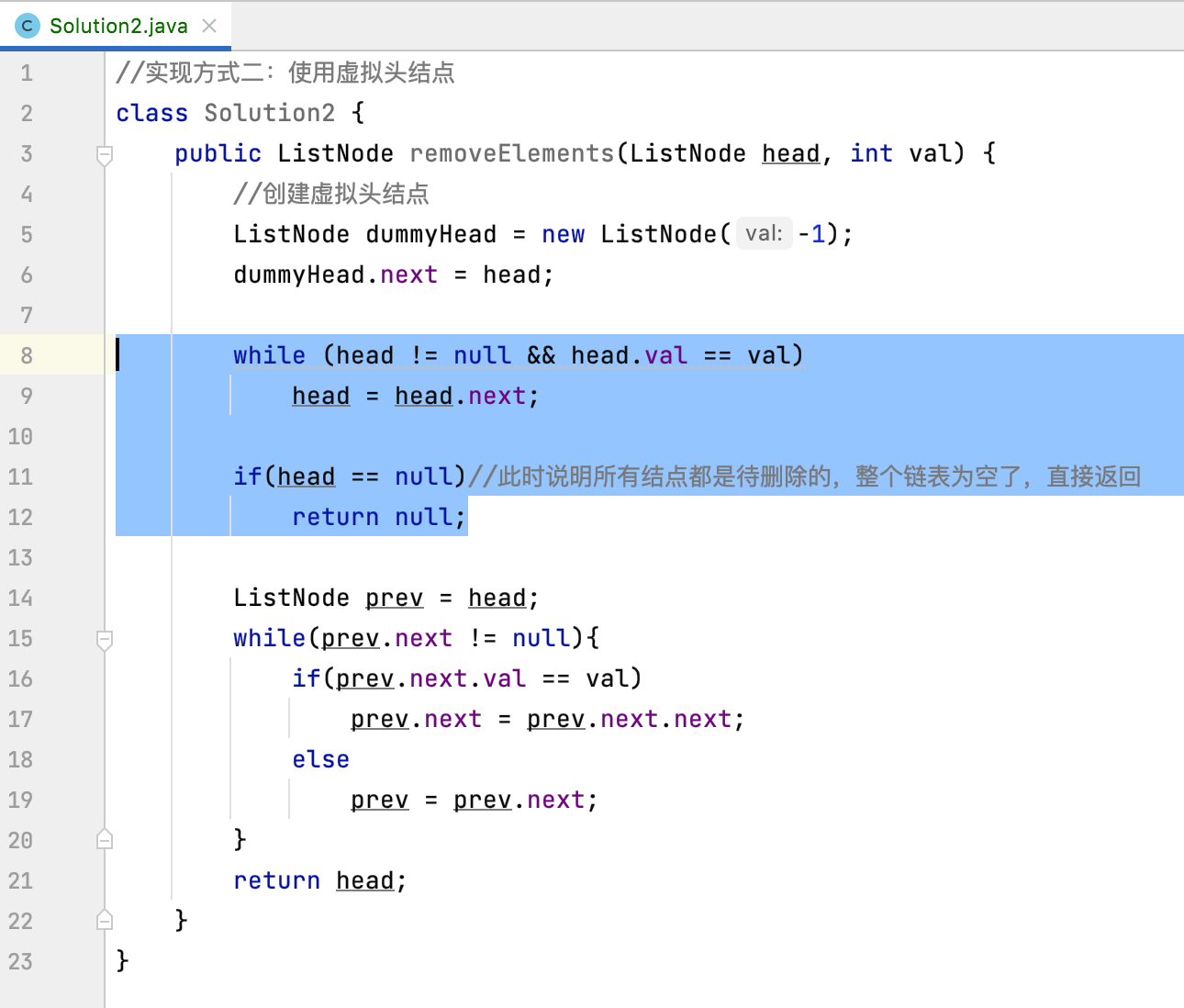
此时代码就精简为:
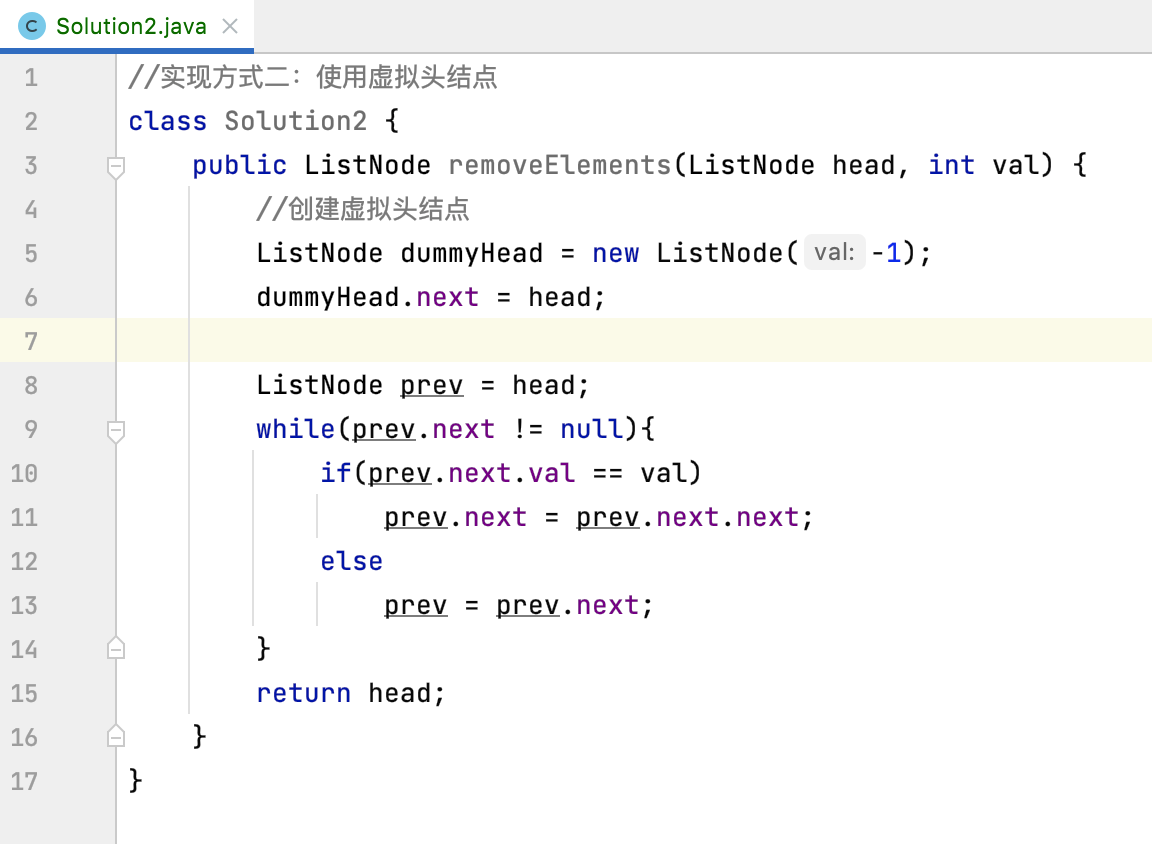
然后再改一个小点整个逻辑就完成,那就是:
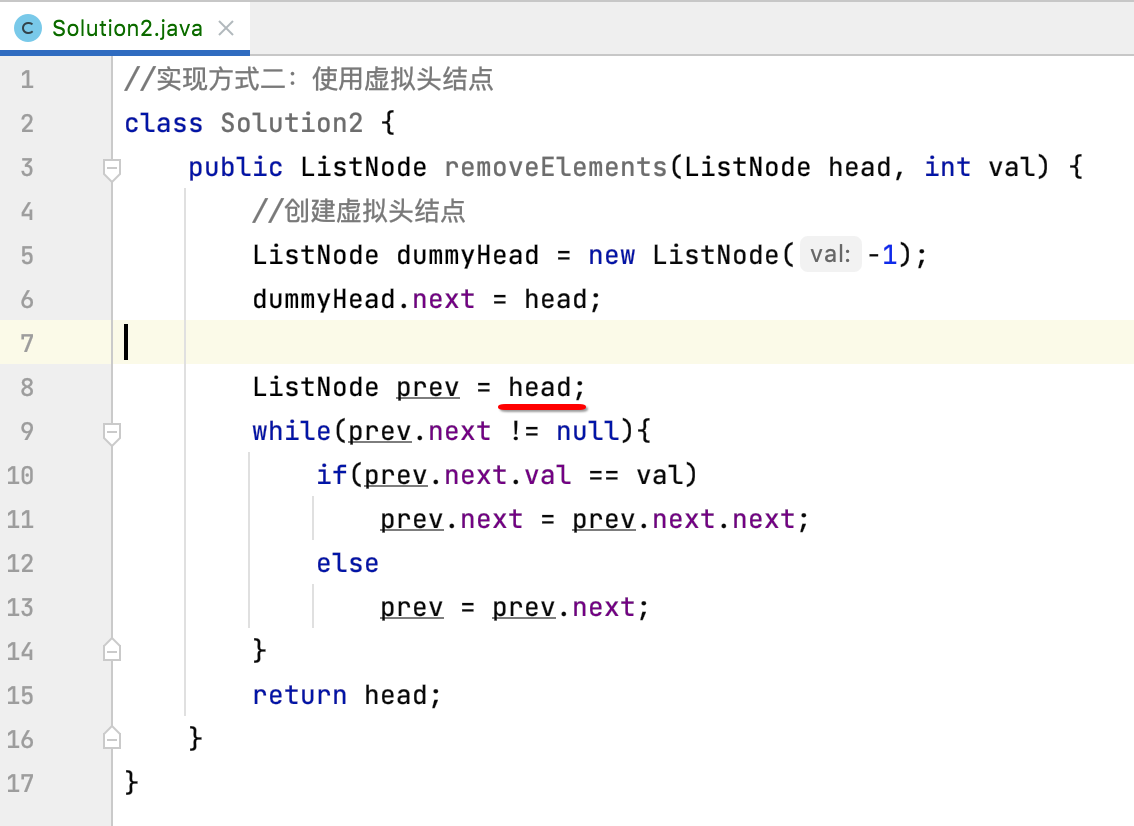
改为虚拟头结点既可:

最后,不要忘了改这:
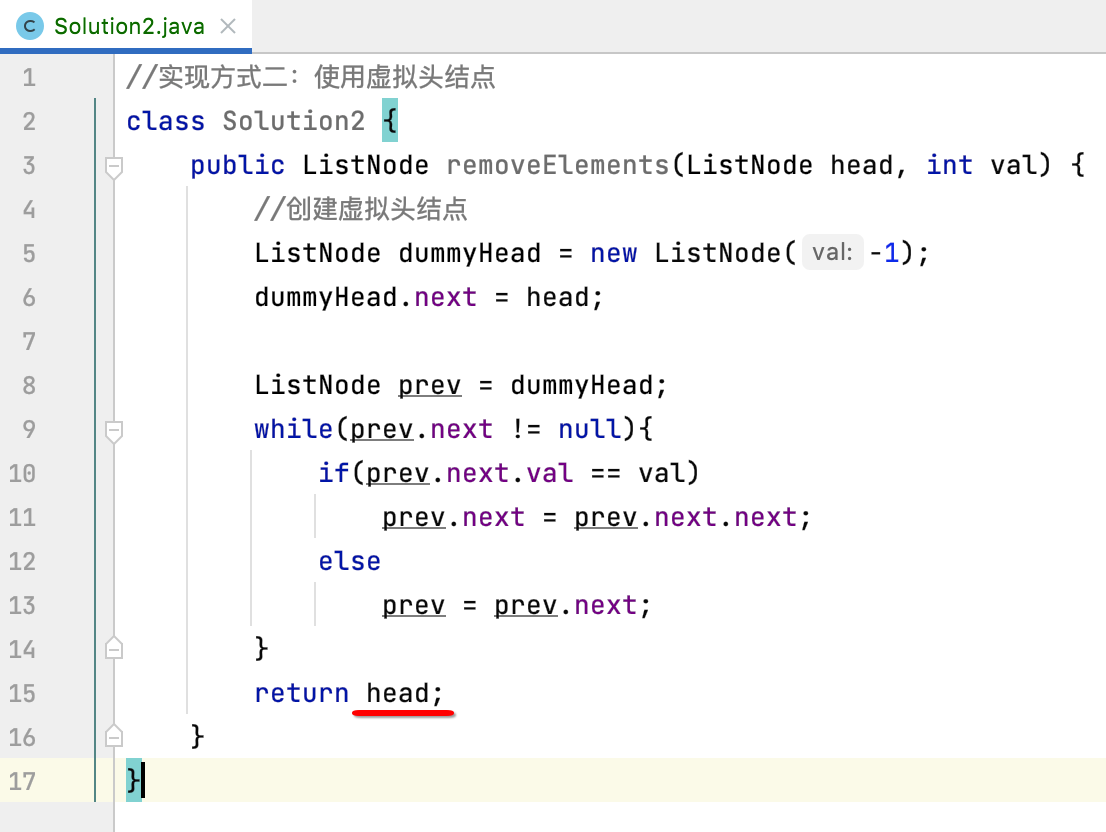
为它:
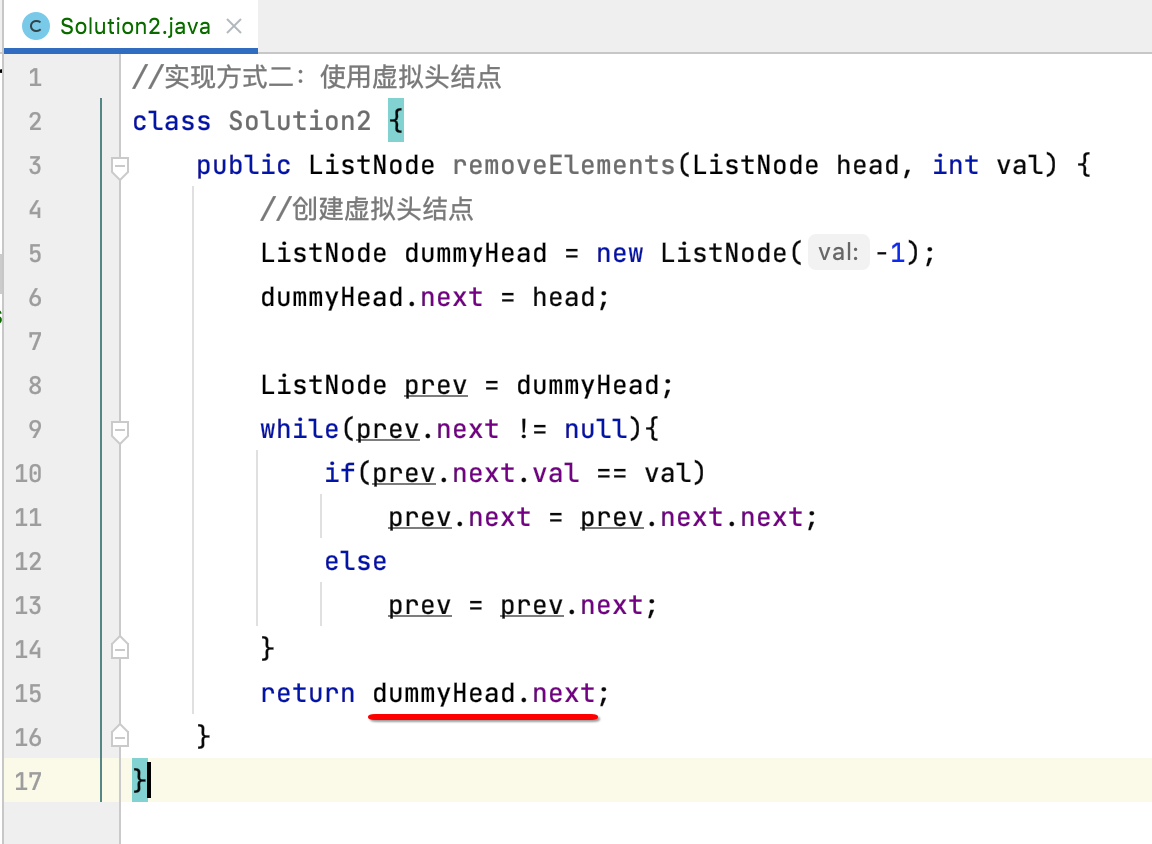
体会到了使用虚拟头结点之后对于我们编写逻辑是不是变得更加的清晰简单?接下来再提交看一下结果:
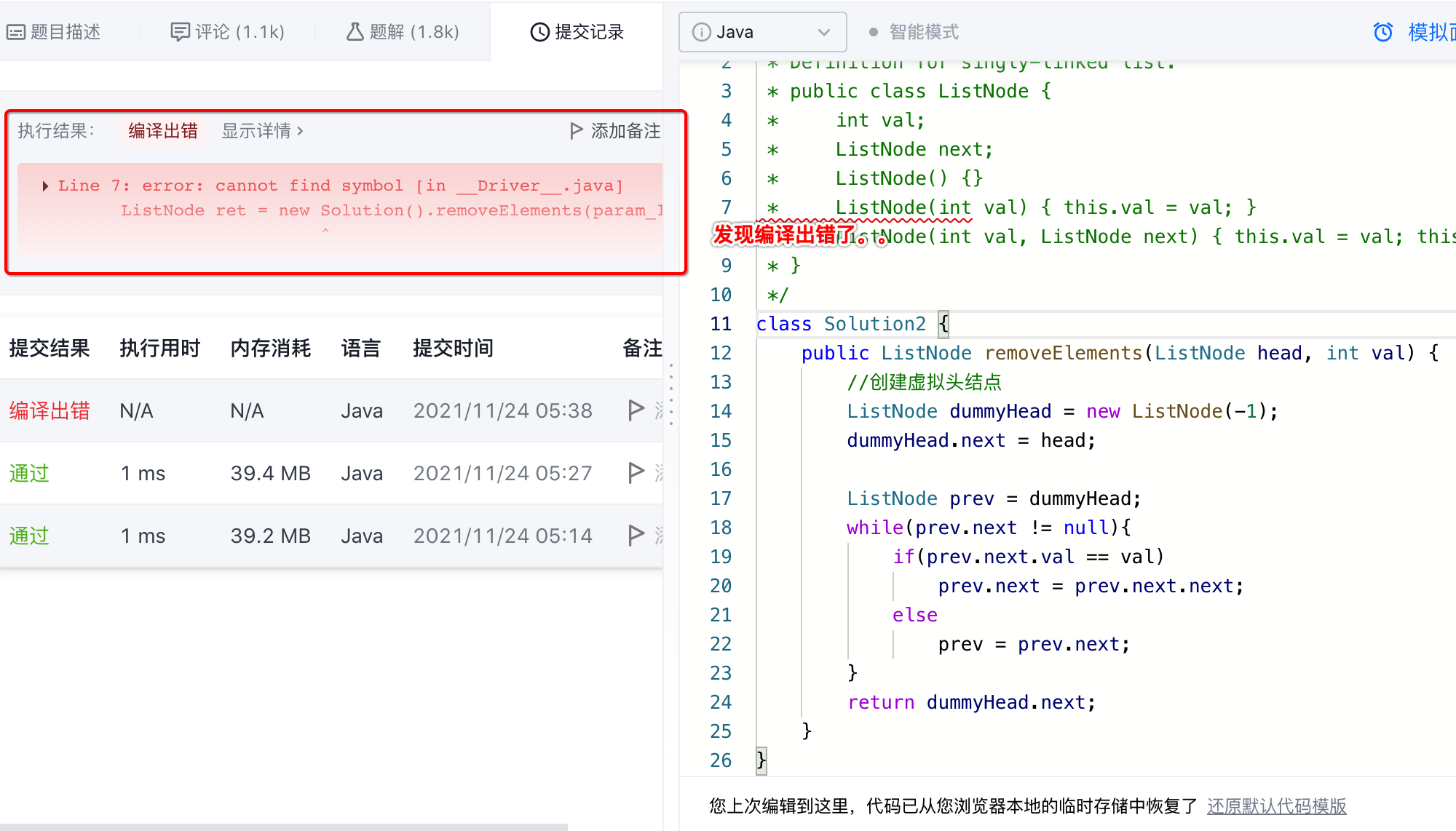
原因是由于我们的类名叫Solution2,而LeetCode中的给的模板类名为Solution,所以这块需要注意了,类名完全不能更改的,咱们改回来再提交一下:
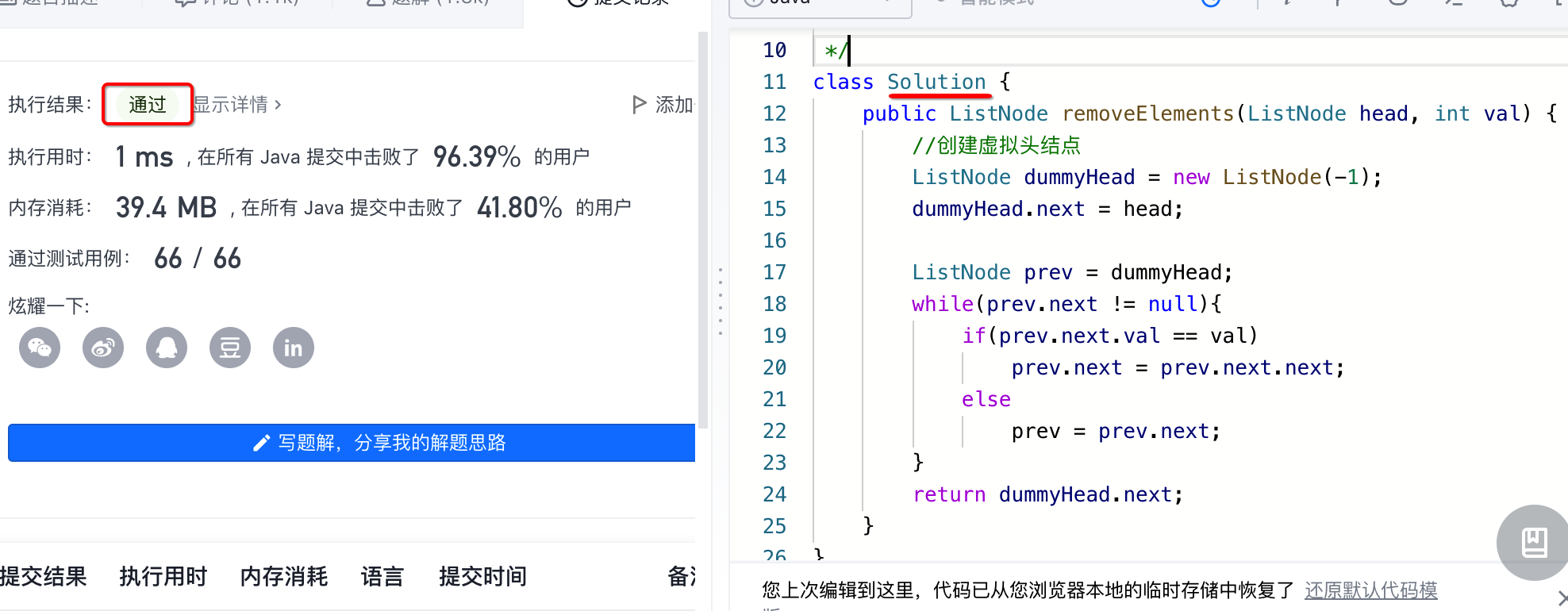
测试自己的Leetcode链表代码:
在咱们这次LeetCode的编写代码中,发现都没有本机进行调试,直接就把结果给贴到LeetCode中了,这貌似不符合正常的代码逻辑编写流程,哪有写了代码不本地测试运行就能知道自己写出来的逻辑就是完成对的呢?所以接下来就来看一下如何来在本机测试LeetCode中这个链表题的代码,很显然先创建main方法:
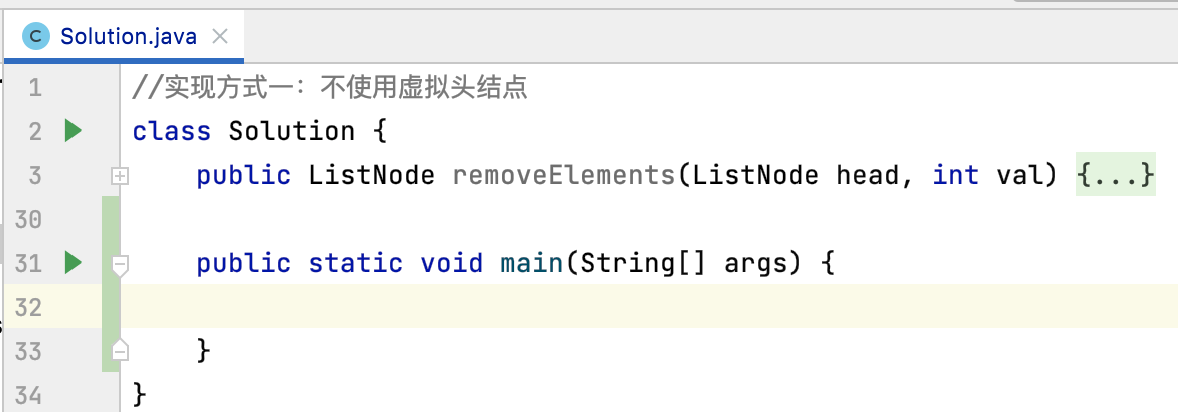
然后接下来需要先来构建一个链表才行,假设要构建的链表元素为:
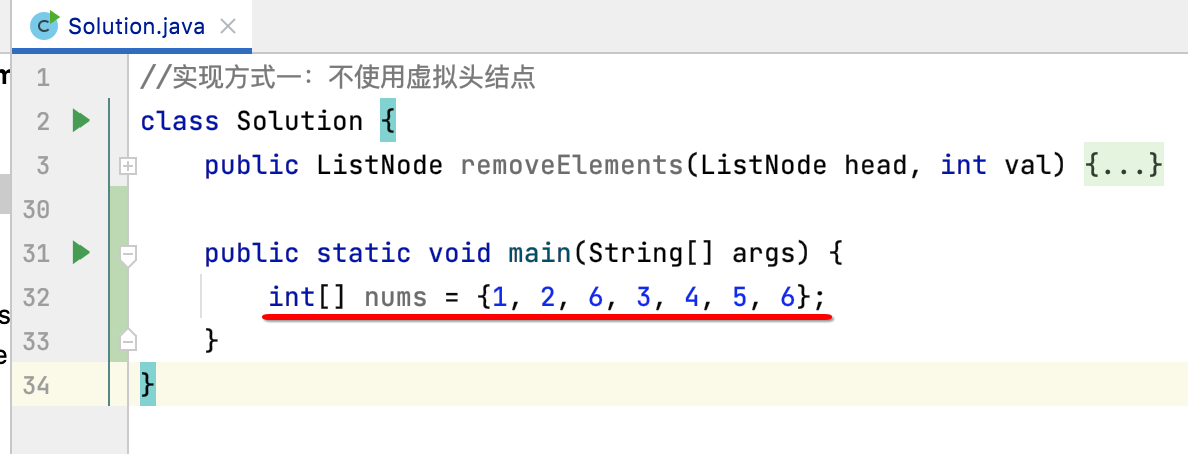
此时就需要将其转换成一个链表,这里在ListNode中定义一个方法来实现它,比较简单:
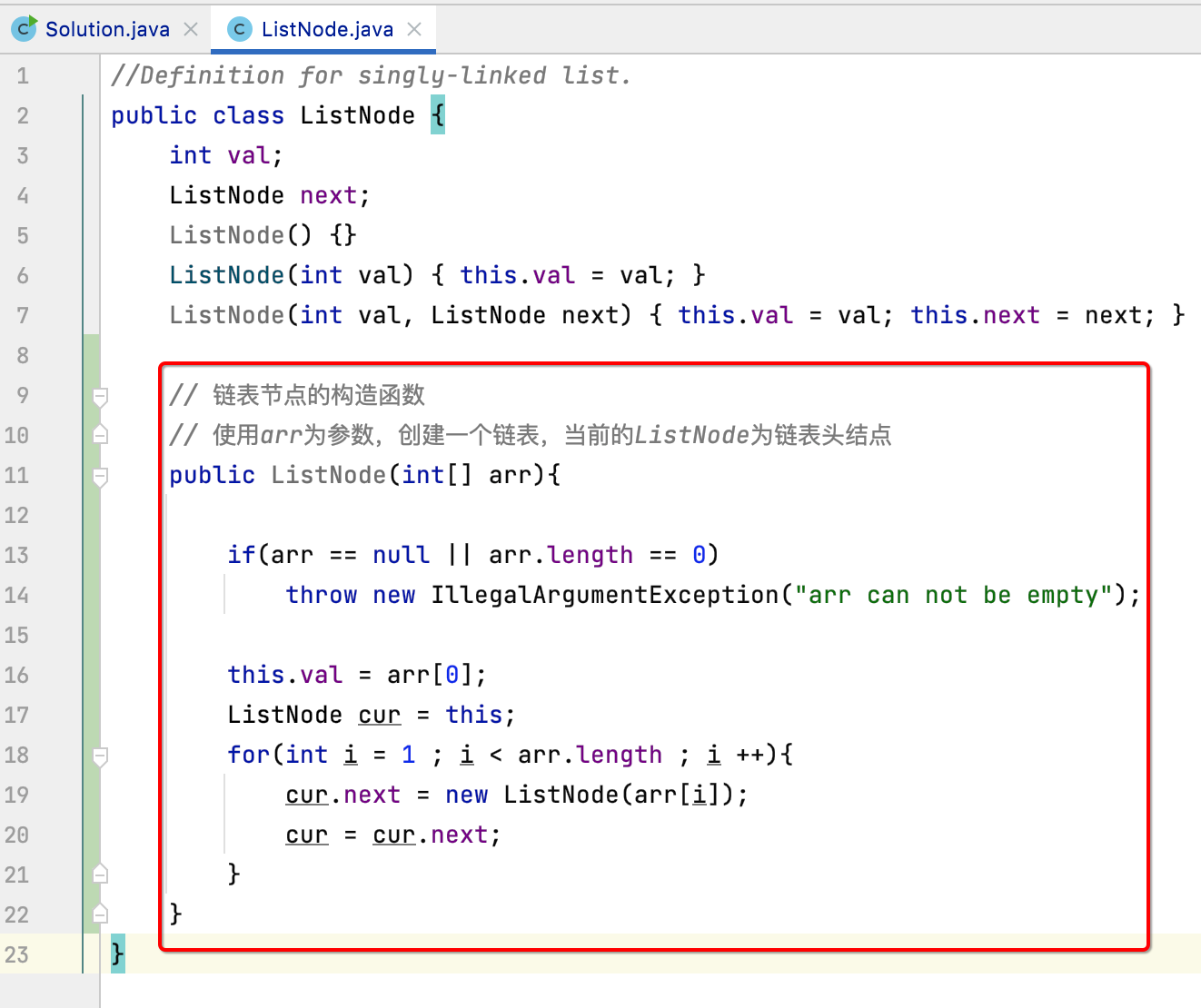
为了方便看到整个链表的情况,覆写一下toString():
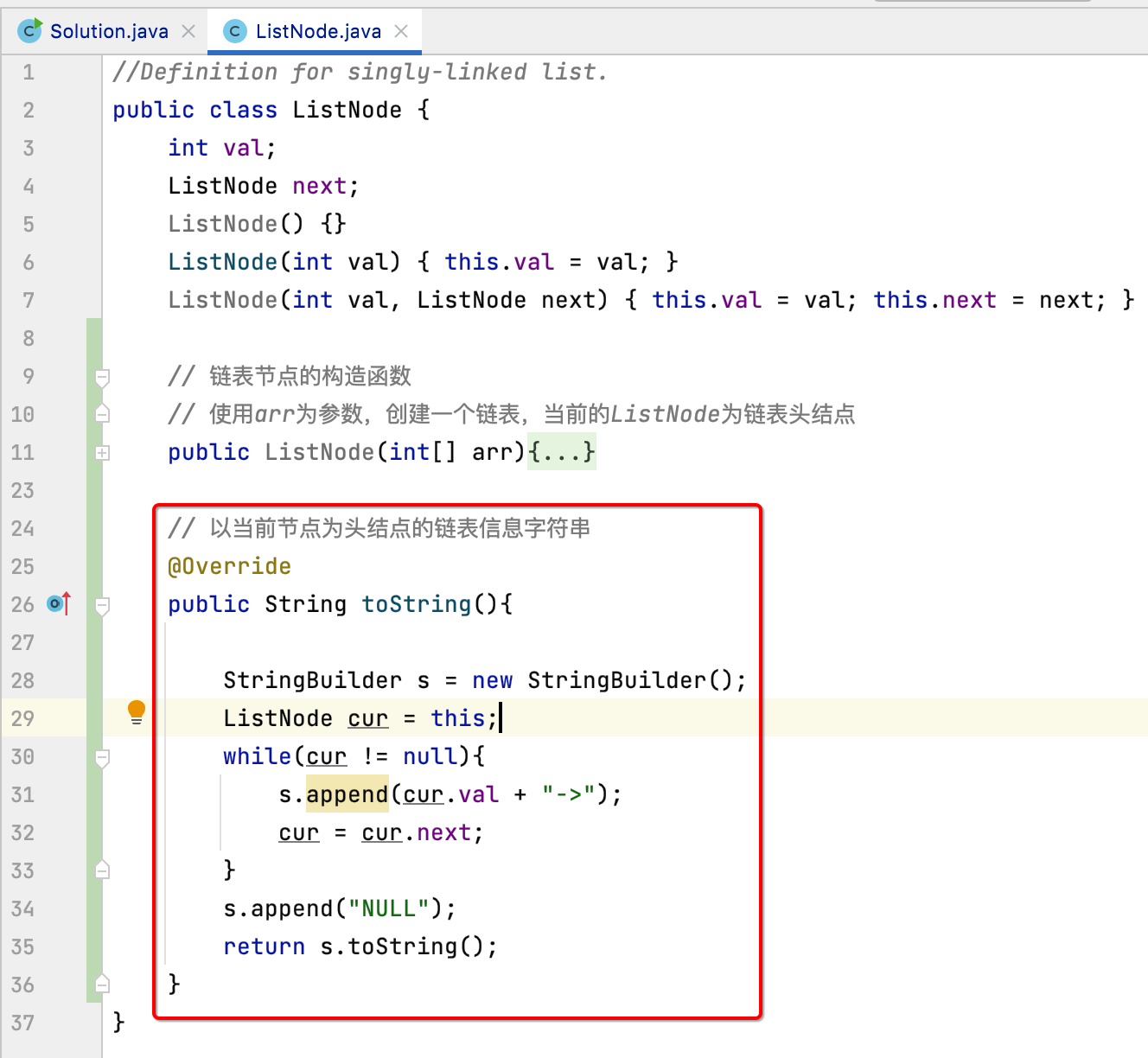
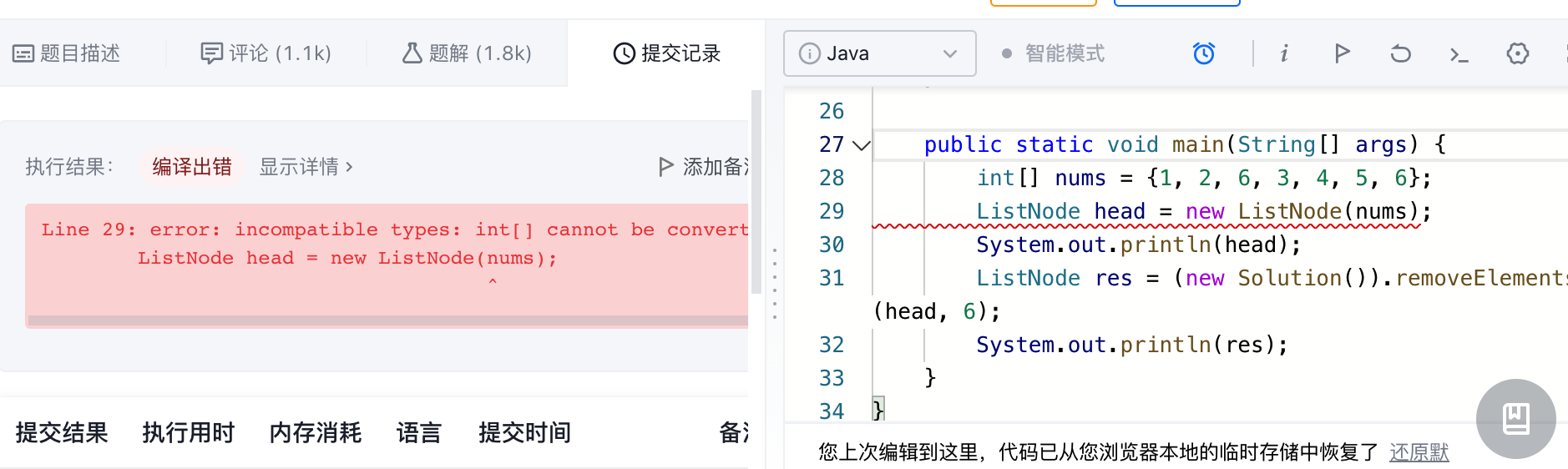
接下来咱们就可以进行main函数的测试用例的编写了,如下:

同样的代码,我们可以放到Solution2中也测试一下:

不过有一个注意点,就是当本地测试代码通过之后,记得提交至LeetCode时要将这个main()函数给删掉,不然会掉错的:
递归基础与递归的宏观语意:
好,终于回到主题来了,关于递归在计算机领域中是非常重要组建组件逻辑的机制,在以后算法的学习中你也将能体会到几乎都与递归相关,通常递归的代码也比较难懂,所以,打好递归的基础是尤为重要的,这里的主题应该是研究链表与递归的关系对吧,但是这里先从递归的基础概念着手,了解透了递归它的语意之后再来研究链表与递归它们之间的关系这样学起来会平滑很多。
递归基础:
本质上递归它就是将原来的问题,转化为更小的“同一”问题,比如拿数组求和来说,比如数组有n个元素,求它们之间的和:
![]()
是不是此时它可以等价于第一个元素+之后的所有元素的和?如下:
![]()
其中,体会一下:

只是:
![]()
其中前面的Sum是对n个元素进行求和,而后面的Sum是对n-1个元素求和,是不是第二个Sum它解决的是更小的同一个问题?
同样的,这里还可以让它的问题变得更小:
![]()
如下:

以此类推,这里一定要理解“更小的同一个问题”它的含义,更小的最后,你会发现就成这样了:

而一个空数组的和不就是为0么,当最基本的问题解决之后,就可以回溯,最终来解决原问题了。
以上就是对于递归它的一个非常直观的理解,但是对于一个数组求和需要用到这么“重”的递归么?事实是不需要的,直接怼一个循环就可以了,但是!!!这是让我们用一个最简单的程序来直观理解递归程序的一个非常好的方式。
实践:递归数组求和
接下来咱们则回到代码,先来手动实现咱们的第一个递归程序,当然每个人对于递归也是比较熟了,只是在于能否比较好的使用递归的区别了,而要用好递归必须得先打好基础,所以练一练有益无害:
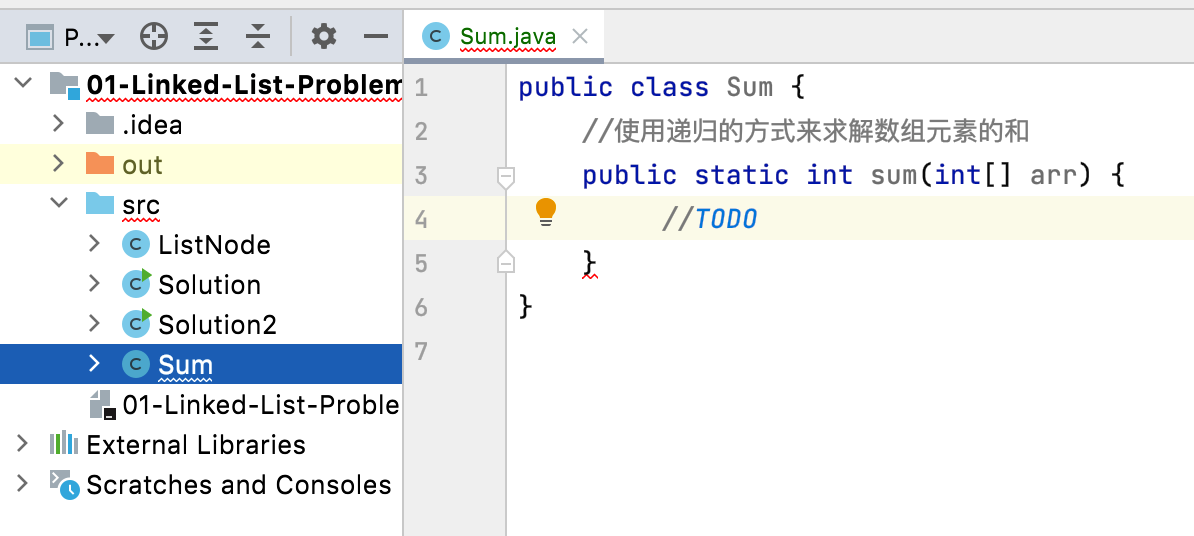
然后递归的思想在于一点点来缩小这个数组的大小对吧,而缩小的关键在于应该指定一下数组的开始元素在哪对吧,所以这里需要再定义一个私有的方法来为这个递归的实现做准备:
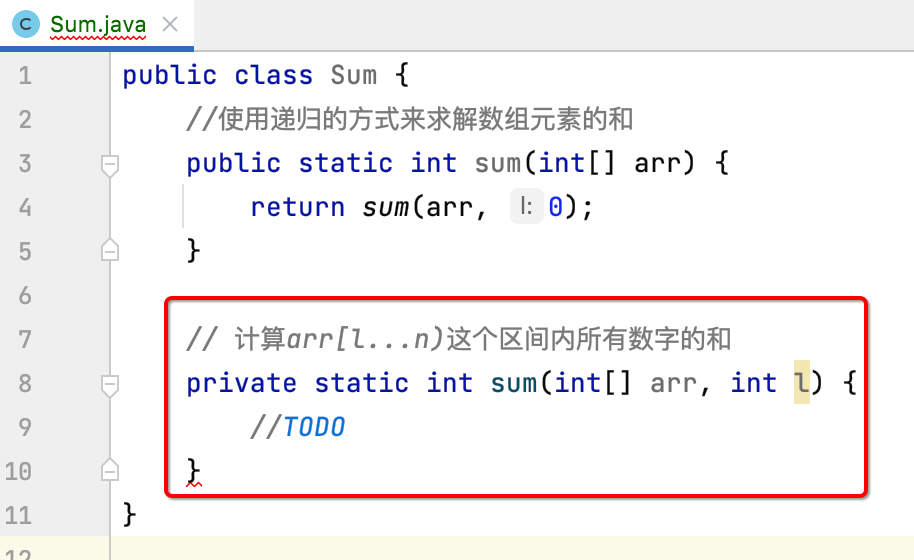
也就是对于初始的情况下,是计算从数组的第0到n-1个位置上的和对吧,接下来递归的体现就在这个私有方法中,对于递归我们知道必须需要有一个条件用来结束递归对吧,所以首先来写终止条件:
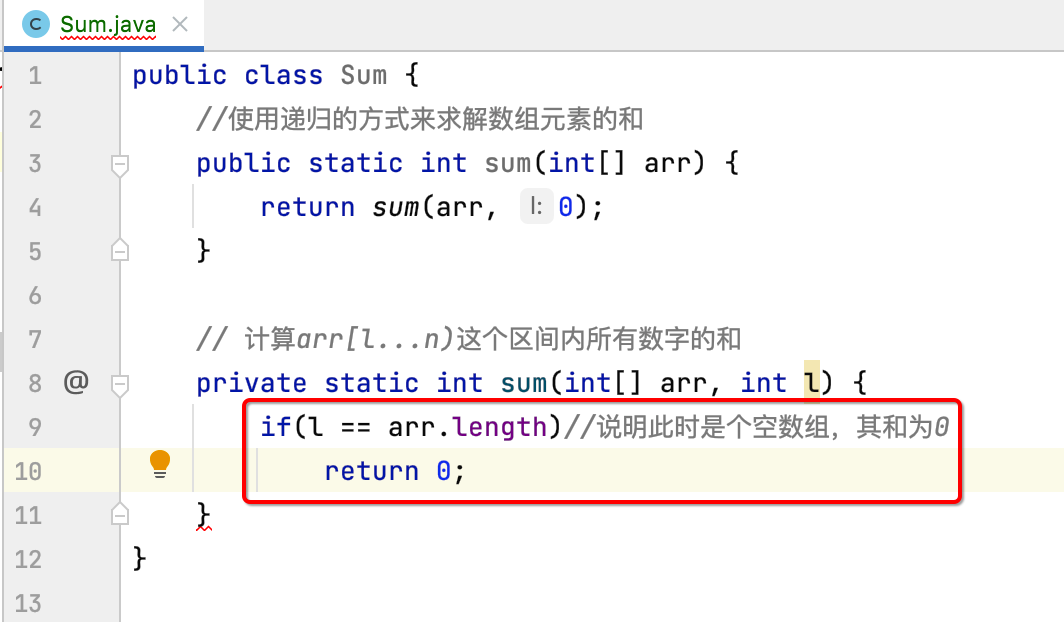
接下来就是递归代码了,这个递归比较简单,如下:
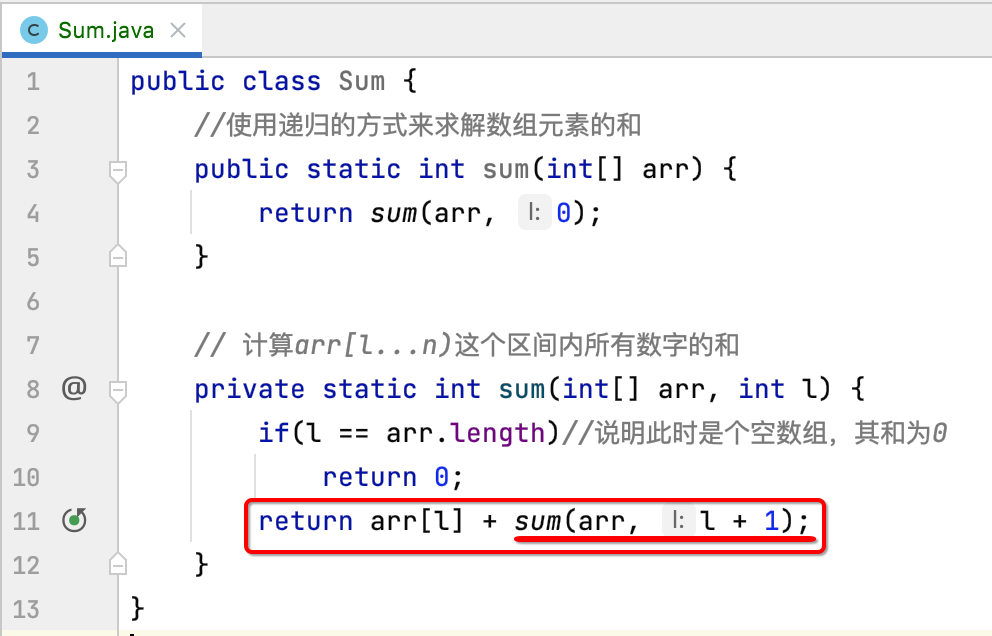
接下来调用测试一下:
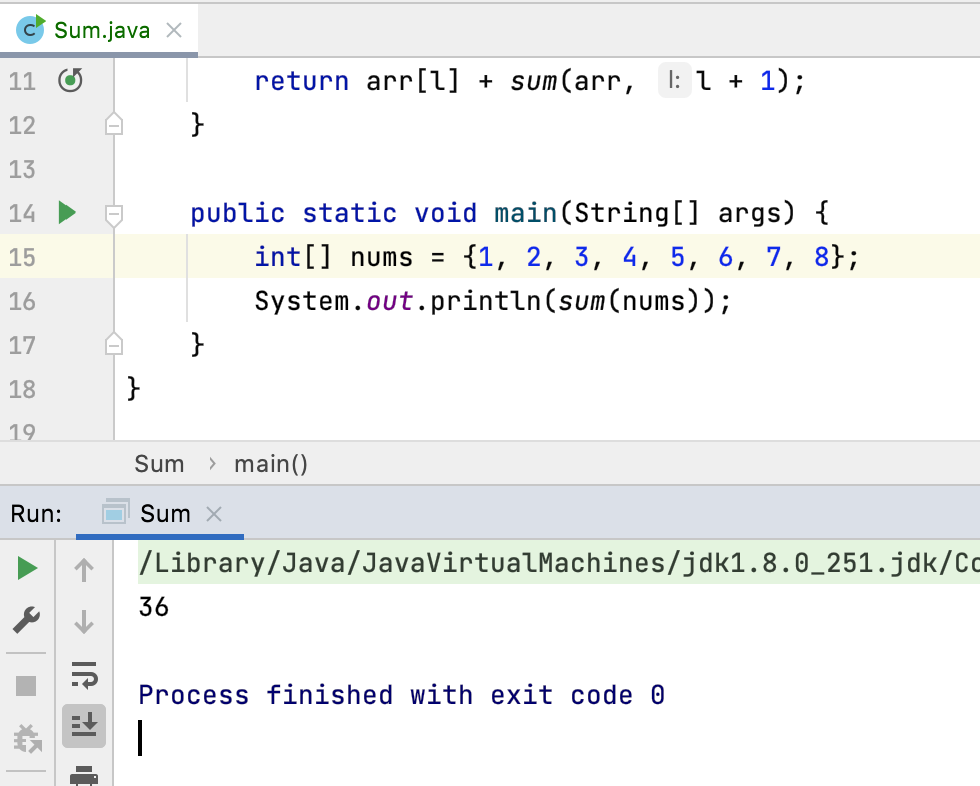
递归的宏观语意:
对于这种小菜级别的递归没啥好说的,人人都会,重点是通过简单的程序来对递归的概念有一个比较深刻地认识才行,通过这个小程序,其实要写好一个递归需要两步骤:

这两步骤是缺一不可的,先把握一个原则。对于目前咱们这个递归程序理解起来是非常容易,但是!!!实际真正递归发生它的作用是在一个非常复杂的逻辑当中,那个时候你不一定就能非常清晰的读懂这个递归函数的逻辑了,原因是主要是函数里面又调函数,非常之晕,因为大多数人所在意的是整个递归程序调用的一个机制【在之后也会完整的分析这个程序的运行机制的】,而其实要摆脱这种困境那就需要注重递归函数的“宏观”语意,啥意思?对于这个函数,它所干的事情就是“计算arr[l...n)这个区间内所有数字的和”对吧,这就是一个宏观语意,在这个语意下, 我们就不要把递归当作是一个算法,而是将它当作一个函数,是用来完成一个功能的,如果一个函数A里面它调用了另一个函数B此时是不是不会晕? 而一旦是函数A里面又调用了函数A此时就晕了,也就是:
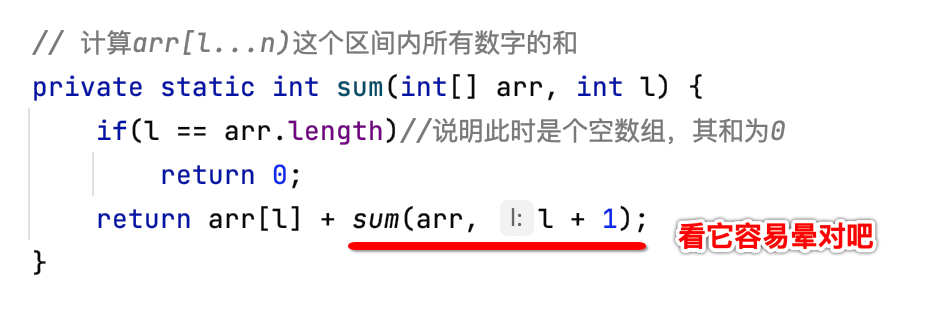
不要去微观的纠结它的整个背后执行的过程,它是如何调用,而是要从宏观的角度把它当成是一个子函数,现在要干的事就是利用这个子函数来构建自己的逻辑,来解决整个函数的功能问题,这样从宏观的角度来实现递归就会让我们理解变得轻松一些。
关于递归后面还得不断操练,这里算是一个开端,打了一个小基础,由于篇幅有限,下次继续。