这次学习一个新的非常重要的概念:"堆",先不急着编码,先用理论对它进行一个详细的阐述,所以这篇是纯理论的东东,在学习"堆"概念之前,先要解决一个问题:怎么将一个二叉树放到一个数组里面呢?之前是用链表来存放二叉树的,用数组怎么表达这种连接的关系呢?
完全二叉树:
这里用一个简单的二叉树为例---完全二叉树,因为完全二叉树是非常适合存放在数组当中的,所以这里又得去学习一下什么是完全二叉树,百度百科一下:


其中标红的部份也提到了,堆实际上就是一种完全二叉树,所以首先得了解完全二叉树的概念,那上面的文本定义实际还是有些抽象,下面看张对比图:
从上面的对比图可以对完全二叉树有个感性的认识:

另外还有一个特点就是:
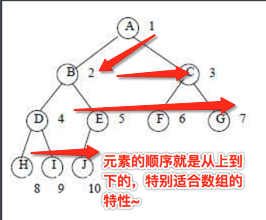
那到底如何存放完全二叉树结点呢?继续看图:

也就是逐层遍历二叉树的元素,然后按顺序去一个个存放,那二叉树是有一个父子元素的关系的,那对于一个父结点,如何知道它的左右两他子元素呢?其实它们是有规律可循,如下:

下面来找下规律:
对于7在数组存放的position=2,而它的子元素6的position=5=2*2[也就是父元素存放的位置]+1、子元素4的position=6=2*2[也就是父元素存放的位置]+2;
同样对于11在在数组存放的position=0,而它的子元素10的position=1=2*0[也就是父元素存放的位置]+1、子元素7的position=2=2*0[也就是父元素存放的位置]+2;
所以对于i个元素,它的左右子节点在数组的位置分别为:2*i+1、2*i+2。
那脑补一下,对于不完全二叉树,如果用数组来存放会有什么问题呢?当然是中间有很多空的元素啦,所以说对于不完全二叉树最好不是用链表来存储~
二叉堆【heap】:
了解了完全二叉树之后,接下来就来阐述下什么是二叉堆,先来百度百科一下:

而对于最大堆和最小堆的表现,可以看下图所示:

那对于上图我们说的完全二叉树实际上就是一个最大堆:
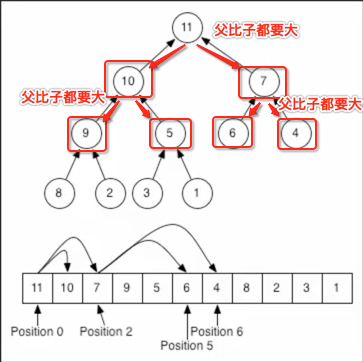
【注意】:堆【heap】不一定就是说的二叉堆,它有很多种表示,但是基本上堆都有这样类似的特性,只是说由二叉树表示的堆称为二叉堆。
二叉堆的操作:
插入元素:
对于二叉堆来说,要插入一个新元素其整个过程是怎么样的呢?这里还是以我们之前的那个二叉堆进行说明,以插入"9"为例:

目前肯定不满足二叉堆的要求,父接点6是小于新插入的节点9的,所以两者进行位置交换:

同样的思路,父节点7比子节点9要小,所以需要调换位置:

至此元素插入完成,也符合二叉堆父元素大于子元素的规则,从添加过程中可以发现:只需更改待比较的元素,其它的任何元素位置不需要动,所以效率还是很高的。
删除元素:
这里以删除根结点为例【因为删除根节点是最重要的,所以以它为例】,整个过程如下:

这时当然是不符合二叉堆的规则,接着这样来做:

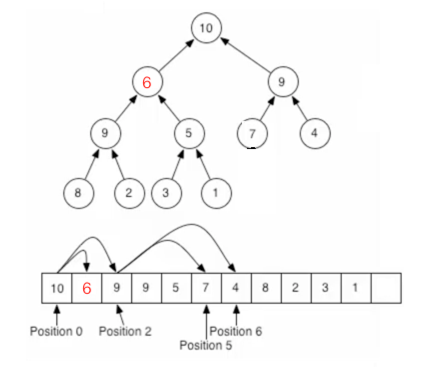
同理继续进行处理:


继续:


经过这些动作之后就将一个根结点给删除掉了,可以发现其实跟插入一个元素一样,只需更改待比较的元素,其它的任何元素位置不需要动,那像这种每次移除掉最大的值有啥用呢?堆排序就产生了,因为每次从根节点拿肯定是最大的数【以最大堆来说】,这样拿出来的数就成了一个有序的数列了。
这次的理论非常重要,虽说有点空谈,但是理解了这些概念才能让我们在之后更复杂的算法中更好的去掌握它们,加油!