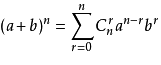因为最近上概率论的时候,发现概率论已经变形了,再也不是概率论,他现在已经变成高数了,哇,还要求二重积分。。高数可能是数学的基础把。于是我觉得把高数再拿出来看看,希望温故后,以后还能愉快的学习数学。
教材是高等教育出版社,同济大学数学系,我发现好多数学教材都是同济的。同济这么牛逼嘛。
第一章讲函数与极限,看过来后没发现什么特别值得注意的。
但是在书上发现一个很有趣的函数。狄利克雷函数。
明显是一个周期函数,但是却没有最小正周期,而任何一个有理数都是周期。
我百度了一下,发现这个函数确实好有趣。
基本性质
2、值域为{0,1}
3、函数为偶函数
4、无法画出函数图像,但是它的函数图像客观存在
分析性质
1、处处不连续
2、处处不可导
3、在任何区间内黎曼不可积
4、函数是可测函数
还有我在书上p11页发现一个证明题。
设函数f(x)的定义域为(-l,l)证明必存在(-l,l)上的偶函数g(x)和奇函数h(x)使得
f(x)=g(x)+h(x)
证明过程很简单:
证明:假设存在,则
f(x)=g(x)+h(x) 一式
f(-x)=g(-x)+h(-x),即 f(-x)=g(x)-h(x) 二式
一二式相加除以二得 g(x)=[f(x)+f(-x)]/2
h(x)=[f(x)-f(-x)]/2
经验证g(x)为偶函数,h(x)为奇函数,命题得证
这个定理对于一个函数定义域只要关于y轴对称,任何函数都可以写成一个偶函数和一个奇函数相加的形式,虽然不知道有什么用,但是感觉这个定理还是蛮有意思的。
这个之前好像就没有教,后来也没怎么用到,粗略的看了一下,稍微了解一下定义和双曲函数和反双曲函数图像的绘制还是蛮有意思的,因为是关于e的函数,我后来百度后,果然双曲在物理上有好多应用,e这个东西,还是蛮奇妙的。可惜我大学没有学物理,对于高中之后的物理了解甚少。
无穷小
这章很多定理都是明显的,但是好多类似的定理重复了一遍又一遍,很多东西虽然是两个主体,但是概念都是可以适用的,但是却重复很多遍同一个原理对于不同对象,感觉这样没什么意义,反而会让人看的更累。无穷小这个东西还是很有意思的,个人感觉,尤其是对于等价无穷小的疯狂替换。感觉很有意思。因为lim(x->0)x/sinx =1 x和sinx等价了,后面几道例题看下来,感觉可以把一些很麻烦的式子直接替换(以前学的时候怎么就没发现呢!)如sinx和tanx是一样的 ,都是x, cosx是-x。很特别。像(A+x^2)^(1/3)-1 直接看出是1/3x^2是等价的。并且在后面也得到了证明。(x->0)(1+x)^a-1 ~ax 的,(x->0) e^x~x ,In(1+x)~x 但是没有做很多题目做实验,这个规律也只能是小猜测把。因为最终目标是掌握二重积分。。所以不在此做过多猜测实验。。以后要是有时间可以再研究。
还有连篇赘述的函数连续性和一些其他定理,都是结合图像后很明显的规律,书上花费篇幅太长不值得。
顺便在记一下两个重要的极限
lim(x->0)( sinx /x )=1 ; lim(x->无穷)(1+ 1/x)=e
后者的证明用到了牛顿二项式定理,我开始都不知道这是啥,证明感觉太过混乱,不想再看,但是 二项式定理还是很简单明了的,感觉二项式定理应用面还是很广泛的。在此 记录一下二项式定理。