地址:http://poj.org/problem?id=1177
题目:
Picture
| Time Limit: 2000MS | Memory Limit: 10000K | |
| Total Submissions: 12905 | Accepted: 6817 |
Description
A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.
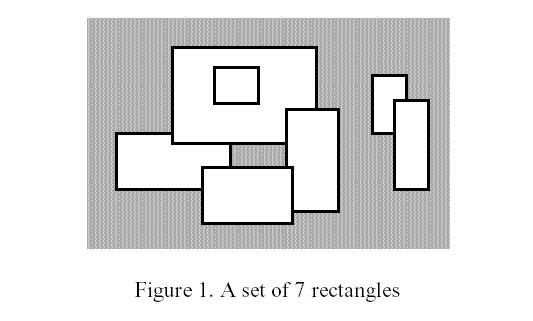
The corresponding boundary is the whole set of line segments drawn in Figure 2.
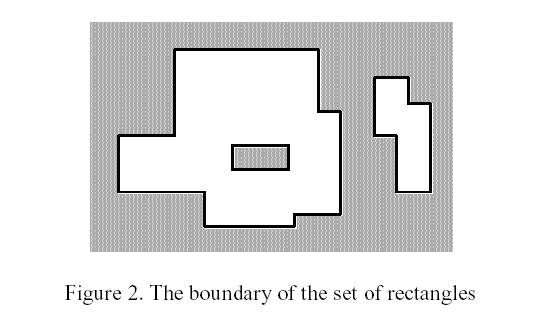
The vertices of all rectangles have integer coordinates.
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.

The vertices of all rectangles have integer coordinates.
Input
Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
Output
Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.
Sample Input
7 -15 0 5 10 -5 8 20 25 15 -4 24 14 0 -6 16 4 2 15 10 22 30 10 36 20 34 0 40 16
Sample Output
228
Source
思路:
复习下。。。
1 #include <cstdio> 2 #include <algorithm> 3 #include <cstring> 4 #include <cmath> 5 6 using namespace std; 7 8 #define MP make_pair 9 #define PB push_back 10 #define lc (o<<1) 11 #define rc (o<<1|1) 12 typedef long long LL; 13 typedef pair<int,int> PII; 14 const double eps=1e-8; 15 const double pi=acos(-1.0); 16 const int K=5e3+7; 17 const int mod=1e9+7; 18 19 struct node 20 { 21 int l,r,y,f; 22 bool operator < (const node &ta)const 23 { 24 return y<ta.y; 25 } 26 }seg[K*2]; 27 int cover[K*8],sum[K*8],lp[K*8],rp[K*8],cnt[K*8]; 28 int hs[K*2]; 29 void push_up(int o,int l,int r) 30 { 31 if(cover[o]) 32 sum[o]=hs[r+1]-hs[l],lp[o]=rp[o]=cnt[o]=1; 33 else if(l==r) 34 sum[o]=lp[o]=rp[o]=cnt[o]=0; 35 else 36 { 37 sum[o]=sum[lc]+sum[rc]; 38 lp[o]=lp[lc],rp[o]=rp[rc]; 39 cnt[o]=cnt[lc]+cnt[rc]-(rp[lc]&lp[rc]); 40 } 41 } 42 void update(int o,int l,int r,int nl,int nr,int f) 43 { 44 if(l==nl&&r==nr) 45 cover[o]+=f,push_up(o,l,r); 46 else 47 { 48 int mid=l+r>>1; 49 if(nr<=mid) update(lc,l,mid,nl,nr,f); 50 else if(nl>mid) update(rc,mid+1,r,nl,nr,f); 51 else update(lc,l,mid,nl,mid,f),update(rc,mid+1,r,mid+1,nr,f); 52 push_up(o,l,r); 53 } 54 } 55 int main(void) 56 { 57 int n; 58 while(~scanf("%d",&n)&&n) 59 { 60 int tot=0,ans=0; 61 memset(cover,0,sizeof cover); 62 memset(lp,0,sizeof lp); 63 memset(rp,0,sizeof rp); 64 memset(cnt,0,sizeof cnt); 65 memset(sum,0,sizeof sum); 66 for(int i=1,lx,ly,rx,ry;i<=n;i++) 67 { 68 scanf("%d%d%d%d",&lx,&ly,&rx,&ry); 69 seg[tot+1]=(node){lx,rx,ly,1}; 70 seg[tot+2]=(node){lx,rx,ry,-1}; 71 hs[tot+1]=lx,hs[tot+2]=rx; 72 tot+=2; 73 } 74 sort(seg+1,seg+1+tot); 75 sort(hs+1,hs+1+tot); 76 int sz=unique(hs+1,hs+1+tot)-hs,ls=0; 77 for(int i=1;i<=tot;i++) 78 { 79 int l=lower_bound(hs+1,hs+sz,seg[i].l)-hs; 80 int r=lower_bound(hs+1,hs+sz,seg[i].r)-hs; 81 update(1,1,sz,l,r-1,seg[i].f); 82 ans+=abs(ls-sum[1]); 83 if(i!=tot) 84 ans+=2*cnt[1]*(seg[i+1].y-seg[i].y); 85 ls=sum[1]; 86 } 87 printf("%d ",ans); 88 } 89 return 0; 90 }