Exploiting Edge Features in Graph Neural Networks

介绍

现如今图神经网络取得了很大进展，最典型的两个模型是GCN模型和GAT模型，然而现有的图神经模型仍然存在以下两个问题：

1. 边特征未被有效考虑。比如GAT只考虑两个节点之间是否有边(binary indicator)，GCN的边特征只能是一个实数(one-dimensional real value)，通常表示权重
2. GAT和GCN在每一层都基于最开始输入的邻接矩阵进行节点特征过滤，而原始的邻接矩阵可能是有噪声，不是最佳的

因此，这篇文章提出一个新的学习框架来增强GCN和GAT，具体的创新点可以概括为如下：

• 提出了一个能够利用多为边特征的框架，克服了上述的GAT和GCN的缺点
• 使用双重随机(doubly stocahstic)对边归一化，这显示出更好的去噪性能
• 设计了一种新的基于注意力的图网络架构，该架构不仅可以过滤节点特征，还可以跨层适应边特征
• 提出了一种编码边方向信息方式，便于学习有向图网络

模型细节

模型架构

给定包含(N)个节点的图，(X in mathbb{R}^{N imes F})表示节点特征，(E in mathbb{R}^{N imes N imes P})是边特征，其中(E_{ijcdot}=mathbf{0})表示节点(i,j)直接没有边连接。文章所提出的模型如下图所示：

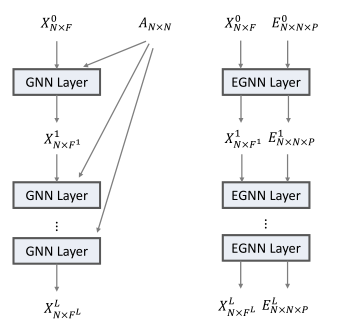
双随机正则化(Doubly stocahstic normalization)

本中使用边特征乘以节点特征的方式过滤节点特征，因此为了避免乘积导致输出特征尺度发生变化，边特征需要被正则化。正则化的方式如下：

[ ilde{E}_{ijp} = frac{hat{E}_{ijp}}{sum_{k=1}^N hat{E}_{ikp}} \ ]

[E_{ijp} = sum_{k=1}^N frac{ ilde{E}_{ikp} ilde{E}_{jkp}}{sum_{v=1}^N ilde{E}_{vkp}} ]

这样做完之后，边特征满足下面条件，即每行每列之和分别都是1：

[E_{ijp} geq 0 ]

[sum limits_{i=1}^N E_{ijp} = sum limits_{j=1}^N E_{ijp} = 1 ]

EGNN(A),基于Attention的EGNN层

为了利用多维边特征，这篇文章提出了如下聚合操作：

[X^l = sigma left[ mathop{||} limits_{p=1}^P left(alpha_{cdot cdot p}^l(X^{l-1}, E^{l-1}_{cdot cdot p})g^l (X^{l-1}) ight) ight] ]

其中(sigma)是激活函数，(alpha)是一个产生(N imes N imes P)张量的函数，(alpha_{cdot cdot p})表示其第(p)个通道切片，(g)是节点特征变换函数。

(alpha^l)就是所谓的注意力系数，(alpha_{ijp})是(X_{icdot}^{l-1})，(X_{jcdot}^{l-1})和(E_{ijp})的函数，其中(E_{ijp})就是边特征的第(p)个通道。对于多维特征，EGNN将之看作多通道信号，每一个通道会产生单独的Attention操作，不同通道结果直接连接。对于一个特定的通道(p)，Attention操作如下：

[alpha_{cdot cdot p}^l=DS( ilde{alpha}_{cdot cdot p}^l) ]

[ ilde{alpha}_{ijp}^l = f^l(X_{icdot}^{l-1},X_{jcdot}^{l-1})E_{ijp}^{l-1} ]

其中，(DS)就是双随机正则化，(f)可以是任何接受两个向量作为输入，输入一个标量值的Attention函数，例如：

[f^l(X_i^{l-1},X_j^{l-1}) = exp left{ L (a^T[WX_{icdot}^{l-1} || WX_{jcdot}^{l-1}]) ight} ]

其中(L)是leakyReLU，(W)是映射矩阵，(||)是连接操作。

因为文章中边特征适用于过滤节点特征的，所以对于下一层，直接将attention系数作为边特征：

[E^l = alpha^l ]

EGNN(C)，基于卷积的层

[X^l = sigma left[ mathop{||} limits_{p=1}^P (E_{cdot cdot p}X^{l-1}W^l) ight] ]

有向图的边特征

对于有向图，EGNN将通道(E_{ijp})拓展成三个通道：

[[E_{ijp}, E_{jip}, E_{ijp} + E_{jip}] ]

分别代表了前向，反向和无向信息。这样在编码时，节点就会从三类邻接点中聚合信息。