最小联结词组

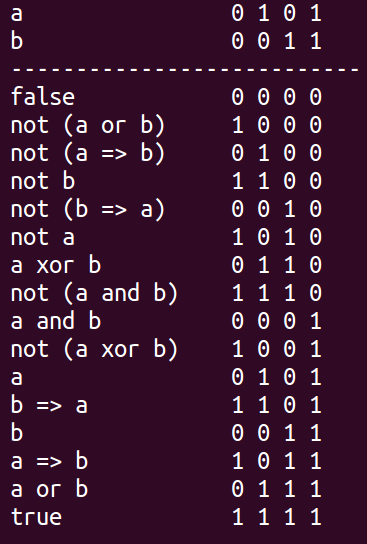
This is only ok in Binary Logic.
有17个最小联结词组(如果认为包含true和false的不是最小联结词组，那么最小联结词组只有11个)

not(or)        |
not(=>)        |not            |
not(and)       |
not            |and            |
not(=>)        |not(xor)       |
false          |and            |not(xor)       |
xor            |and            |not(xor)       |
false          |=>             |
not(=>)        |=>             |
not            |=>             |
xor            |=>             |
not            |or             |
false          |not(xor)       |or             |
xor            |not(xor)       |or             |
not(=>)        |true           |
xor            |and            |true           |
xor            |or             |true           |

整理一下

not(or)
not(and)

not,or
not,and
not,=>
not,not(=>)

not(=>),=>
not(=>),true 
not(=>),not(xor)  
=>,false
=>,xor

xor,and,not(xor)
xor,or,not(xor)
xor,and,true  
xor,or,true

not(xor),and,false
not(xor),or,false  

xor功能比false更丰富，因为false = a xor a，所以一切出现false的地方都可以用xor取代

I got this result by a violent method:If you run this program ,you can see more things.

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<list>
using namespace std;
const int N = 1 << 16;//There are 65536 probability.
bool a[16][4]; //A 10 B 12
const char *desc[16] = { "false", "not (a or b)",
"not (a => b)", "not b",
"not (b => a)", "not a",
"a xor b", "not (a and b)",
"a and b", "not (a xor b)",
"a", "b => a",
"b", "a => b",
"a or b", "true" };
const char*desc_simple[16] = { "false", "not(or)", "not(=>)", "not", "not(=>)", "not", "xor", "not(and)", "and", "not(xor)", "a", "=>", "b", "=>", "or", "true" };
/*
上表中，只有条件运算符和非条件运算符是不满足交换律，但是它们是等价的
也就是说：2，4等价，11，13等价,3,5等价
*/
int eq[] = { 2, 4, 11, 13, 3, 5 }, eq_size = 3;
void init(){//初始化16个逻辑词
	for (int i = 0; i < 16; i++){
		int x = i;
		for (int j = 0; j < 4; j++){
			a[i][j] = x & 1;
			x >>= 1;
		}
	}
}
void show(int n){
	printf("	%-16s", desc[n]);
	for (int i = 0; i < 4; i++)printf("%2d", a[n][i]);
	puts("");
}
void table(){
	show(10), show(12);//10和12代表着原始的a和b
	puts("	---------------------------");
	for (int i = 0; i < 16; i++)show(i);
}

int ans[N], ai = 0;//存储全部的答案
int book[N][16][3];//对于N中逻辑词组，16个逻辑词来源于三个人：a，b，操作 
//判断集合set是否是完备的逻辑词组
bool ok(int n){
	int temp = n;
	n |= (1 << 10) | (1 << 12);
again:
	for (int i = 0; i < 16; i++)
	if (n&(1 << i))
	for (int j = 0; j < 16; j++)
	if (n&(1 << j))
	for (int k = 0; k < 16; k++)
	if (n&(1 << k)){
		//i,j分别操作数，k表示操作符，也就是k表示运算法则
		int t = 0;//t表示运算结果
		for (int l = 0; l < 4; l++)//将四位分别进行运算
			t |= (a[k][a[i][l] + a[j][l] * 2] << l);
		if ((n&(1 << t)) == 0){
			n |= (1 << t);
			book[temp][t][0] = i, book[temp][t][1] = j, book[temp][t][2] = k;
			goto again;
		}
	}
	return n == N - 1;
}
void print(bool detail){
	for (int i = 0; i < ai; i++){
		int n = ans[i];
		for (int j = 0; j < 16; j++){
			if (n&(1 << j)){
				const char*des = detail ? desc[j] : desc_simple[j];
				printf("%-15s|", des);
			}
		}
		puts("");
		if (detail){
			for (int i = 0; i < 16; i++){
				if ((n&(1 << i)) || i == 10 || i == 12)continue;
				printf("		%-15s = %-15s [%-15s] %-15s
", desc[i], desc[book[n][i][0]], desc[book[n][i][2]], desc[book[n][i][1]]);
			}
			puts("");
		}
	}
}
//根据eq数组去掉等价的元素
void simple(){
	for (int i = 0; i < ai; i++){
		int n = ans[i];
		for (int j = 0; j < eq_size; j++){
			if (n&(1 << eq[j << 1 | 1])){
				n &= ~(1 << eq[j << 1 | 1]);
				n |= (1 << eq[j << 1]);
			}
		}
		ans[i] = n;
		for (int j = 0; j < i; j++)
		if (ans[i] == ans[j])
			ans[i] = -1;
	}
	int ind = 0;
	for (int i = 0; i < ai; i++)
	if (ans[i] != -1)ans[ind++] = ans[i];
	ai = ind;
}
bool visited(int x){
	for (int i = 0; i < ai; i++)
	if ((ans[i] & x) == ans[i])
		return true;
	return false;
}
int main(){
	init();
	table();//打印表，说清逻辑运算及其对应的编码
	memset(book, -1, sizeof(book));
	for (int i = 0; i < N; i++){
		//先判断i的某个子集是否已经是最小逻辑词组，如果是，则i必然不是最小逻辑词组
		if (visited(i))continue;
		if (ok(i)) ans[ai++] = i;
	}
	simple();
	print(false);
	return 0;
}