一个正方体盒子,把它展开成平面,有多少种展开方法?
给定一个平面(由若干个小正方形组成),问这个平面能否折成正方体?
下面给出更清晰的定义:
给定一个6×6的方格图,每个方格标识0,1表示是否选择这个方格,问选中的这些方格能否折成正方形?
一开始,我是这么想的:

给最上最左的小方格标上“上”,从这个小方格按照上表进行广搜。每个小方格都有一个“坐标系统”,表示它的上下左右各是哪个方向。最上最左小方格的坐标系统是任意的。
另一种方法:
f[当前状态][当前状态从哪个方向来][当前状态到哪个方向去]=下一状态
一种有24种状态×4种操作
下面回到第一个问题,一个正方体有多少种展开方法?(正方体各个面都相同,各个面都等价,也就是说,只考虑展开之后所得平面的形状)
正方体有12条边,展开成平面只剩下5条边。
正方体有8个顶点,每个顶点对应三条边,这3条边不能同时属于这5条边。
1:141型.只要是141型,无论1怎么排都可以.共5种
2:231型.共3种
3:33型,只有一种.必须是第一排和第二排首尾相连.
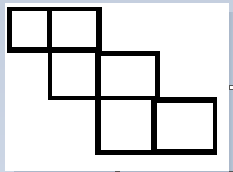
4:222型,必须呈阶梯状.只有1种.

更复杂的问题:
给定平面上若干个面(每个面用多边形表示),问这个平面能否折成封闭的三维体?
给定一个封闭的三维体,问它有多少种展开方法?