导航:复试上机历年真题,题目未搜集全
十四:2003 十三:2004
十二:2005 十一:2006
十:2007 九:2008
八:2009 七:2012
六:2013 五:2014
四:2015 三:2017
二:2018 一:2019
十二、2005
1、蛇形填数
题目:
方阵填数:在一个 n* n 的数组中,填入 1,2,3,….N* N 个数,并要求按如下格式输出该数组的元素,例如一个 5* 5 的数组输出顺序为:
代码:
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
using namespace std;
const int maxn=11;
int num=1;
int a[maxn][maxn]={0};
//输入5的时候
//13 14 15 16 1
//12 23 24 17 2
//11 22 25 18 3
//10 21 20 19 4
// 9 8 7 6 5
int main()
{
int n, k, i, j;
int x, y;
scanf("%d", &n);
k = 1; x = 1;
y = n;
a[x][y] = 1;
while(k<n*n)
{
while(x+1<=n&&(a[x+1][y]==0))
a[++x][y] = ++k;
while(y-1>=1&&(a[x][y-1]==0))
a[x][--y] = ++k;
while(x-1>=1&&(a[x-1][y]==0))
a[--x][y] = ++k;
while(y+1<=n&&(a[x][y+1]==0))
a[x][++y] = ++k;
}
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
printf("%4d", a[i][j]);
printf("
");
}
return 0;
}
2、集合M
题目:
编程,按递增次序生成集合 M 的最小的 100 个数并输出之。M 的定义为:①1∈M②X∈M,则 2X+1∈M 且 3X+1∈M;显然 M 是一无限集合,M={1,3,4,7,9,…}
代码:
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
using namespace std;
const int maxn = 10000;
int M[100]={0}, p[maxn]={1};
int num=0;
int main()
{
int i;
fill(p, p+maxn, 1);
p[1] = 0;
for(i=1;i<=1000;i++)
{
if(p[i]==0&&num<100)
{
M[num++] = i;
p[2*i+1] = 0;
p[3*i+1] = 0;
}
}
for(i=0;i<100;i++)
printf("集合M中的第%d个位%d
", i+1, M[i]);
return 0;
}
3、二叉树
题目:
编程实现:要求建立一颗二叉树以二叉链表存储,输出要求的树状编号。结点结构为
lchild-data-num-rchild
其中二叉树的 num 编号域为整数类型 ,data 数据域为字符类型。
要求生成二叉树中编号,从一开始进行连续编号,每个结点的编号大于其左右孩子的编号,同一个结点的左右孩子中,其左孩子的编号小于其右孩子的编号。
请给出对二叉树中结点的实现如上要求并按如下右图树状实现编号的程序。
测试数据:输入 AB∪D∪∪CE∪F∪∪∪(其中符号∪代表空格)
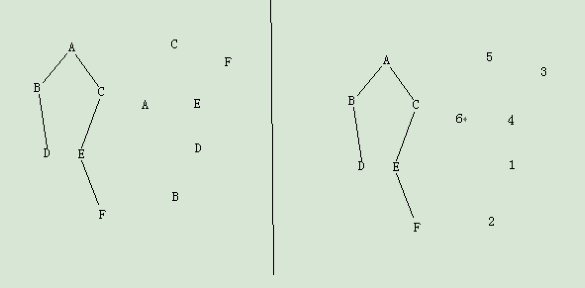
思路:
- 创建一二叉排序树
- 二叉排序树中左孩子节点data小于根节点data小于右孩子节点data值
- 但是节点编号大于左右编号,因此在编号的时候采用后序

代码:
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
using namespace std;
typedef struct BTNode
{
struct BTNode *Lchild, *Rchild;
char Data;
int Num;
}BTNode, *BTree;
int num=1;
void preCreatBTree(BTree *bt)
//先序创建二叉树
{
char ch;
ch = getchar();
if(ch==' ')
*bt = NULL;
else
{
BTNode *p = new BTNode;
p->Data = ch;
*bt = p;
preCreatBTree(&((*bt)->Lchild));
preCreatBTree(&((*bt)->Rchild));
}
}
void layerPrint(BTree bt, int layer)
//树状打印
{
if(bt!=NULL)
{
layerPrint(bt->Rchild, layer+1);
for(int i=0;i<layer;i++)
printf(" ");
printf("%c,%d
", bt->Data, bt->Num);
layerPrint(bt->Lchild, layer+1);
}
}
void setNumber(BTree bt)
//从一开始进行连续编号,每个结点的编号大于其左右孩子的编号,同一个结点的左右孩子中,其左孩子的编号小于其右孩子的编号
//要用后序遍历
{
if(bt!=NULL)
{
setNumber(bt->Lchild);
setNumber(bt->Rchild);
bt->Num = num++;
}
}
int main()
{
BTree bt;
preCreatBTree(&bt);
setNumber(bt);
printf("层级打印:
");
layerPrint(bt, 0);
return 0;
}