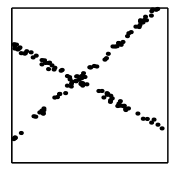
假设有一堆数据点 ,它是由两个线性模型产生的。公式如下:
,它是由两个线性模型产生的。公式如下:
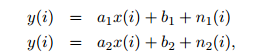
模型参数为a,b,n:a为线性权值或斜率,b为常数偏置量,n为误差或者噪声。
一方面,假如我们被告知这两个模型的参数,则我们可以计算出损失。
对于第i个数据点,第k个模型会预测它的结果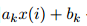
则,与真实结果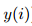 的差或者损失记为:
的差或者损失记为: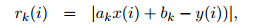
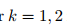
目标是最小化这个误差。
但是仍然不知道具体哪些数据由对应的哪个模型产生的(缺失的信息)。
另一方面,假设我们被告知这些数据对应具体哪个模型,则问题简化为求解约束条件下的线性方程解
(实际上可以计算出最小均分误差下的解,^-^)。
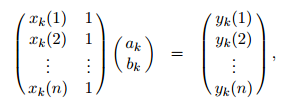
这两个假设,都只知道其中的一部分信息,所以求解困难。
EM算法就是重复迭代上述两步,固定因素A,放开因素B,然后固定因素B,再放开因素A,直到模型收敛,
如此迭代更新估计出模型的输出值以及参数值。
具体如下:
--------------------------------------------------------------------------------------------------------
在E步时,模型参数假定已知(随机初始化或者聚类初始化,后续不断迭代更新参数),
计算出每个点属于模型的似然度或者概率(软判决,更加合理,后续可以不断迭代优化,而硬判决不合理是因为之前的假定参数本身不可靠,判决准则也不可靠)。
根据模型参数,如何计算出每个点属于模型的似然度或者概率?
计算出模型输出值与真实值的残差:
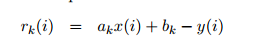
已知残差,计算出i点属于k模型的似然度(残差与似然度建立关系):
贝叶斯展开

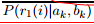 =
= 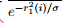 ,假设残差与概率分布为高斯分布,残差距离度量 转换成 概率度量。
,假设残差与概率分布为高斯分布,残差距离度量 转换成 概率度量。
残差越小,则由对应模型生成的概率越大。
根据产生的残差,判断i属于模型k的归属概率
则,

完成点分配到模型的目的
--------------------------------------------------------------------------------------------------------
进入M步,知道各个点属于对应模型的概率,估计出模型参数
绝对值差*概率,误差(均方误差)期望最小化
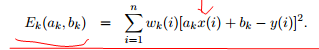 最小化
最小化
求偏导:
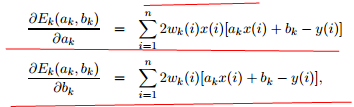
置0,则上述两公式展开为
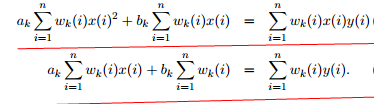
改写成 矩阵式:
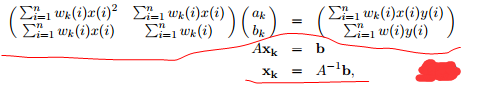
完成计算出ak和bk参数
如此,反复迭代,收敛
EM算法对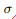 敏感,每轮迭代它的更新推荐公式:
敏感,每轮迭代它的更新推荐公式:
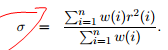
--------------------------------------------------------------------------------

同样地,在 GMM 中,我们就需要确定 影响因子pi(k)、各类均值pMiu(k) 和 各类协方差pSigma(k) 这些参数。 我们的想法是,找到这样一组参数,它所确定的概率分布生成这些给定的数据点的概率最大,而这个概率实际上就等于  ,我们把这个乘积称作似然函数 (Likelihood Function)
,我们把这个乘积称作似然函数 (Likelihood Function)
没法直接用求导解方程的办法直接求得最大值。
不清楚这类数据是具体哪个高斯生成的,或者说生成的概率。
E步中,确定出数据xi属于第i个高斯的概率:通过计算各个高斯分量的后验概率,占比求得。
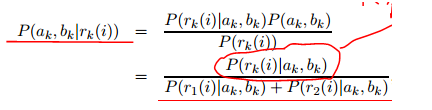
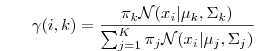
解决了点归属哪个高斯的问题,这是缺失的信息。
M步中,重新计算出各个参数。
根据似然概率最大化,可以推出均值、方差、权重更新公式。
另外知道了各个点属于各个高斯的概率,也可以直接计算求出 均值、方差、权重

如此E步和M步重复。
参考:http://blog.csdn.net/abcjennifer/article/details/8198352
--------------------------------------------------------------------------------------------------------