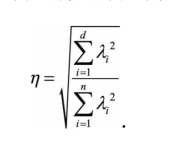1. PCA降维
PCA:主成分分析(Principe conponents Analysis)
2. 维度的概念
一般认为时间的一维,而空间的维度,众说纷纭。霍金认为空间是10维的。
3. 为什么要进行降维?
维度灾难:当维度超过一定值的时候,分类器效果呈现明显下降。
PCA旨在找到数据中的主成分,并利用这些主成分表征原始数据,从而达到降维的目的。举一个简单的例子,在三维空间中有一系列数据点,这些点分布在一个过原点的平面上。如果我们用自然坐标系x,y,z三个轴来表示数据,就需要使用三个维度。而实际上,这些点只出现在一个二维平面上,如果我们通过坐标系旋转变换使得数据所在平面与x,y平面重合,那么我们就可以通过x,y两个维度表达原始数据,并且没有任何损失,这样就完成了数据的降维。而x,y两个轴所包含的信息就是我们要找到的主成分。
4. 目标
提取最有价值的信息(基于方差)
5. 降维后的数据的意义?
降维后物理意义变得模糊,但是不影响我们去后续做分类、预测等的结果。
6. PCA推导过程

7. 结论
- 我们要找最大的方差也就是协方差矩阵最大的特征值;
- 最佳投影方向就是最大特征值对应的特征向量
- 次佳投影方向位于最佳投影方向的正交空间中,是第二大特征值对应的特征向量
求解步骤:
- 对样本数据进行中心化处理
- 求协方差矩阵
- 对协方差矩阵进行特征值分解,将特征值从到小排列
- 取特征值前d大对应的特征向量w1, w2, ..., wd。通过映射关系将n维样本映射到d维空间。
降维后的信息占比定义为: