Andrew Ng机器学习第五章——多变量线性回归

一、多变量线性回归的技巧之一——特征缩放

　　1、为什么要使用特征缩放？

　　　　特征缩放用来确保特征值在相似的范围之内。

　　　　设想这样一种情况（房价预测），两个特征值分别是房子的大小和卧室的数量。每个特征值所处的范围差别很大，其代价函数 的等高线图如下图所示。图像会又瘦又高，这样才利用梯度下降法时需要经过很长时间才会收敛。故使用特征缩短来缩短梯度下降算法的收敛时间。

　　　　

　　

 　　2、特征缩放的基本思想是什么？

　　　　将每一个特征值归一化。例如房子大小x所在的区间是（0,500），将x除以500。这样得到等值图就会比较圆润，梯度下降法也能更快地收敛。

　　　　

　　　　通常将特征值的大小约束在[-1,1]之间。（进行合适的缩放，目的是使图像尽快收敛）

　　　　利用均值归一化使特征值处于（-0.5,0.5）之间：

　　　　　　X := (mean_value - X)/(max - min)

　　　　　　

二、判断是否收敛

1. 　　可以构造迭代次数——代价函数值的图像，通过观察图像判断（该方法可以用来调试学习率α的大小）
2.        设置一个阀值α，当代价函数值小于阀值则说明收敛（通常寻找阀值是一件困难的事）

　　

 

三、正规方程（区别于迭代方法的直接求解）

　　

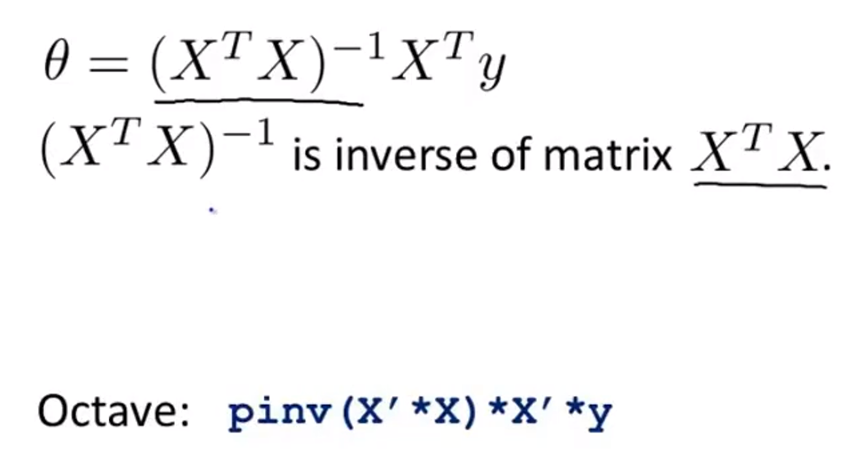
　　正规方程推导：https://blog.csdn.net/rosetta/article/details/74115085

四、选择梯度下降法还是正规方程？

　　两种算法优缺点如下：

　　选择的侧重点主要考虑特征值n的数量.若n很大，上万的数量级，那么选择梯度下降法。否则，选择正规方程。