zoukankan html css js c++ java

wenbao与矩阵

矩阵满足分配率和结合律（非常重要）

****但是不满足交换律

循环矩阵：

　　两个循环矩阵乘积依然是循环矩阵

矩阵乘法

 1 struct mat{
 2     int n, m;
 3     double data[MAXN][MAXN];
 4 };
 5 
 6 int mul(mat& c, const mat& a, const mat& b){
 7     int i, j, k;
 8     if (a.m != b.n)
 9         return 0;
10     c.n = a.n;
11     c.m = b.m;
12     for (i = 0; i < c.n; i++)
13         for (j = 0; j < c.m; j++)
14             for (c.data[i][j] = k = 0; k < a.m; k++)
15                 c.data[i][j] += a.data[i][k] * b.data[k][j];
16     return 1;
17 }

矩阵快速幂

 1 struct Node{
 2     ll x[16][16];
 3 };
 4 Node mul(Node xx, Node yy){
 5     Node X;
 6     for(int i = 0; i < d; ++i){
 7         for(int j = 0; j < d; ++j){
 8             X.x[i][j] = 0;
 9             for(int k = 0; k < d; ++k){
10                 X.x[i][j] = (X.x[i][j] + (xx.x[i][k]*yy.x[k][j])%m) % m;
11             }
12         }
13     }
14     return X;
15 }
16 Node q_m(Node A, ll x){
17     Node AAA;
18     for(int i = 0; i < d; ++i){
19         for(int j = 0; j < d; ++j){
20             AAA.x[i][j] = (i == j);
21             //printf("%lld ", AAA.x[i][j]);
22         }
23         //puts("");
24     }
25     while(x){
26         if(x&1) AAA = mul(AAA, A);
27         A = mul(A, A);
28         x >>= 1;
29     }
30     return AAA;
31 }

--------------------------------------------------------------------------------------------------------------------

矩阵快速幂入门题一：

http://acm.hdu.edu.cn/showproblem.php?pid=1575

直接求矩阵快速幂

 1 #include <iostream>
 2 using namespace std;
 3 #define ll long long
 4 const ll Mod = 9973;
 5 int n;
 6 ll k;
 7 struct Node{
 8     ll x[11][11];
 9 }A;
10 Node mul(Node a, Node b){
11     Node AAA;
12     for(int i = 0; i < n; ++i){
13         for(int j = 0; j < n; ++j){
14             AAA.x[i][j] = 0;
15             for(int k = 0; k < n; ++k){
16                 AAA.x[i][j] = (AAA.x[i][j] + a.x[i][k]*b.x[k][j]%Mod)%Mod;
17             }
18         }
19     }
20     return AAA;
21 }
22 ll q_m(){
23     Node AA;
24     for(int i = 0; i < n; ++i){
25         for(int j = 0; j < n; ++j){
26             AA.x[i][j] = (i == j);
27         }
28     }
29     while(k){
30         if(k&1) AA = mul(AA, A);
31         A = mul(A, A);
32         k >>= 1;
33     }
34     ll sum = 0;
35     for(int i = 0; i < n; ++i){
36         sum = (sum+AA.x[i][i])%Mod;
37     }
38     return sum;
39 }
40 int main(){
41     int t;
42     scanf("%d", &t);
43     while(t--){
44         scanf("%d%lld", &n, &k);
45         for(int i = 0; i < n; ++i){
46             for(int j = 0; j < n; ++j){
47                 scanf("%lld", &A.x[i][j]);
48             }
49         }
50         cout<<q_m()<<endl;
51     }
52     return 0;
53 }

--------------------------------------------------------------------------------------------------------------------

矩阵快速幂入门二：

http://codeforces.com/contest/185/problem/A

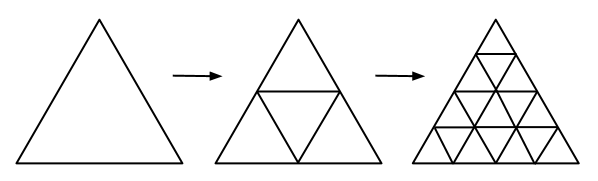
递推上三角形的个数。。。。。。。。。

其实直接推也可以的

 1 #include <iostream>
 2 using namespace std;
 3 #define ll long long 
 4 const ll Mod = 1e9+7;
 5 ll n;
 6 struct Node{
 7     ll x[2][2];
 8 };
 9 Node mul(Node a, Node b){
10     Node AAA;
11     for(int i = 0; i < 2; ++i){
12         for(int j = 0; j < 2; ++j){
13             AAA.x[i][j] = 0;
14             for(int k = 0; k < 2; ++k){
15                 AAA.x[i][j] = (AAA.x[i][j] + a.x[i][k]*b.x[k][j]%Mod)%Mod;
16             }
17         }
18     }
19     return AAA;
20 }
21 ll q_m(ll x){
22     Node AA, A;
23     A.x[0][0] = A.x[1][1] = 3LL;
24     A.x[0][1] = A.x[1][0] = 1LL;
25     AA.x[0][0] = AA.x[1][1] = 1LL;
26     AA.x[0][1] = AA.x[1][0] = 0LL;
27     while(x){
28         if(x&1) AA = mul(AA, A);
29         A = mul(A, A);
30         x >>= 1;
31     }
32     return AA.x[0][0];
33 }
34 int main(){
35     cin >> n;
36     cout<<q_m(n)<<endl;
37     return 0;
38 }

 1 #include <iostream>
 2 using namespace std;
 3 #define ll long long 
 4 const ll Mod = 1e9+7;
 5 ll n;
 6 ll q_m(ll x){
 7     ll xx = 1LL, xxx = 2LL;
 8     while(x){
 9         if(x&1) xx = xx*xxx%Mod;
10         xxx = xxx*xxx%Mod;
11         x >>= 1;
12     }
13     return xx;
14 }
15 int main(){
16     cin >> n;
17     if(n == 0){
18         cout<<1<<endl;
19         return 0;
20     }
21     cout<<(q_m(n-1LL)+q_m(2LL*n-1LL))%Mod<<endl;
22     return 0;
23 }

--------------------------------------------------------------------------------------------------------------------

矩阵快速幂入门三：

http://acm.hdu.edu.cn/showproblem.php?pid=2157

矩阵基本知识关于通路

 1 #include <iostream>
 2 #include <string.h>
 3 using namespace std;
 4 const int Mod = 1000;
 5 int n, m;
 6 struct Node{
 7     int x[22][22];
 8 }A;
 9 Node mul(Node a, Node b){
10     Node AAA;
11     for(int i = 0; i < n; ++i){
12         for(int j = 0; j < n; ++j){
13             AAA.x[i][j] = 0;
14             for(int k = 0; k < n; ++k){
15                 AAA.x[i][j] = (AAA.x[i][j] + a.x[i][k]*b.x[k][j]%Mod)%Mod;
16             }
17         }
18     }
19     return AAA;
20 }
21 void q_m(Node A, int xx, int yy, int zz){
22     Node AA;
23     for(int i = 0; i < n; ++i){
24         for(int j = 0; j < n; ++j){
25             AA.x[i][j] = (i == j);
26         }
27     }
28     while(zz){
29         if(zz&1) AA = mul(AA, A);
30         A = mul(A, A);
31         zz >>= 1;
32     }
33     /*
34     for(int i = 0; i < n; ++i){
35         for(int j = 0; j < n; ++j){
36             printf("%d ", AA.x[i][j]);
37         }
38         cout<<endl;
39     }
40     */
41     printf("%d
", AA.x[xx][yy]);
42 }
43 int main(){
44     while(scanf("%d%d", &n, &m) == 2 && n+m){
45         memset(A.x, 0, sizeof(A.x));
46         while(m--){
47             int xx, yy;
48             scanf("%d%d", &xx, &yy);
49             A.x[xx][yy] = 1;
50         }
51         int t;
52         scanf("%d", &t);
53         while(t--){
54             int xx, yy, zz;
55             scanf("%d%d%d", &xx, &yy, &zz);
56             q_m(A, xx, yy, zz);
57         }
58     }
59     return 0;
60 }

--------------------------------------------------------------------------------------------------------------------

矩阵快速幂入门四

http://poj.org/problem?id=3070

求斐波那契数列

 1 #include <iostream>
 2 #include <stdio.h>
 3 using namespace std;
 4 #define ll long long
 5 const int Mod = 10000;
 6 struct Node{
 7     ll x[2][2];
 8 };
 9 Node mul(Node a, Node b){
10     Node AAA;
11     for(int i = 0; i < 2; ++i){
12         for(int j = 0; j < 2; ++j){
13             AAA.x[i][j] = 0;
14             for(int k = 0; k < 2; ++k){
15                 AAA.x[i][j] = (AAA.x[i][j] + a.x[i][k]*b.x[k][j]%Mod)%Mod;
16             }
17         }
18     }
19     return AAA;
20 }
21 void q_m(ll x){
22     Node AA, A;
23     for(int i = 0; i < 2; ++i){
24         for(int j = 0; j < 2; ++j){
25             AA.x[i][j] = (i == j);
26         }
27     }
28     A.x[0][0] = A.x[0][1] = A.x[1][0] = 1LL, A.x[1][1] = 0;
29     while(x){
30         if(x&1) AA = mul(AA, A);
31         A = mul(A, A);
32         x >>= 1;
33     }
34     /*
35     for(int i = 0; i < 2; ++i){
36         for(int j = 0; j < 2; ++j){
37             printf("%lld ", AA.x[i][j]);
38         }
39         cout<<endl;
40     }
41     */
42     printf("%lld
", AA.x[0][1]);
43 }
44 int main(){
45     int n;
46     while(scanf("%lld", &n) && n != -1){
47         q_m(n);
48     }
49     return 0;
50 }

--------------------------------------------------------------------------------------------------------------------

大牛博客（关于递推构造矩阵）强烈推荐

http://www.cnblogs.com/frog112111/archive/2013/05/19/3087648.html

--------------------------------------------------------------------------------------------------------------------

https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&category=20&problem=1811&mosmsg=Submission+received+with+ID+18912945

　　引用博客　　http://blog.csdn.net/u010304217/article/details/39212049

f[n]=a1*f[n-1]+a2*f[n-2]+...+ad*f[n-d];
由于n太大，不能直接递推，需要用矩阵快速幂来解决，时间复杂度为O(d^3logn)
举例，d=5的矩阵关系式为：
|a1 a2 a3 a4 a5| | f[n] | | f[n+1] |
|1 | | f[n-1] | | f[n] |
| 1 | * | f[n-2] | = | f[n-1] | (空白处为0)
| 1 | | f[n-3] | | f[n-2] |
| 1 | | f[n-4] | | f[n-3] |

矩阵快速幂

 1 #include <iostream>
 2 #include <string.h>
 3 using namespace std;
 4 #define ll long long
 5 ll d, n, m, a[16], f[16];
 6 struct Node{
 7     ll x[16][16];
 8 };
 9 Node mul(Node xx, Node yy){
10     Node X;
11     for(int i = 0; i < d; ++i){
12         for(int j = 0; j < d; ++j){
13             X.x[i][j] = 0;
14             for(int k = 0; k < d; ++k){
15                 X.x[i][j] = (X.x[i][j] + (xx.x[i][k]*yy.x[k][j])%m) % m;
16             }
17         }
18     }
19     return X;
20 }
21 Node q_m(Node A, ll x){
22     Node AAA;
23     for(int i = 0; i < d; ++i){
24         for(int j = 0; j < d; ++j){
25             AAA.x[i][j] = (i == j);
26             //printf("%lld ", AAA.x[i][j]);
27         }
28         //puts("");
29     }
30     while(x){
31         if(x&1) AAA = mul(AAA, A);
32         A = mul(A, A);
33         x >>= 1;
34     }
35     return AAA;
36 }
37 int main(){
38     while(scanf("%lld%lld%lld", &d, &n, &m) && d+n+m){
39         ll xx;
40         for(int i = 0; i < d; ++i) scanf("%lld", &xx), a[i] = xx%m;
41         for(int i = 0; i < d; ++i) scanf("%lld", &xx), f[i] = xx%m;
42         if(n <= d){
43             printf("%lld
", f[n-1]);
44             continue;
45         }
46         Node A;
47         for(int i = 0; i < d; ++i){
48             for(int j = 0; j < d; ++j){
49                 if(i == 0) A.x[i][j] = a[j];
50                 else A.x[i][j] = (i-1 == j);
51                 //printf("%lld ", A.x[i][j]);
52             }
53             //puts("");
54         }
55         Node AA = q_m(A, n-d);
56         ll sum = 0;
57         for(int i = 0; i < d; ++i){
58             sum = (sum + (AA.x[0][i]*f[d-i -1])%m) % m;
59         }
60         printf("%lld
", sum);
61     }
62     return 0;
63 }

--------------------------------------------------------------------------------------------------------------------

https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&category=20&problem=1705&mosmsg=Submission+received+with+ID+2137361

细胞自动机

循环矩阵性质：循环矩阵相乘依然是循环矩阵，且该循环矩阵是对称的。。。。。。。。。

所以可以将　　n^3log(k)　　降为　　n^2long(k)　　因为只要算一行就可以了

做完这个题有个心得，，就是可以将矩阵的下标作为参数传来传去效率高，空间消耗小。。。。。。。牛X

 1 #include <iostream>
 2 #include <stdio.h>
 3 using namespace std;
 4 #define ll long long
 5 ll m[200][550], a[550];
 6 int num, n, d, mod, k;
 7 int mul(int x, int y){
 8     num++;
 9     for(int i = 0; i < n; ++i){
10         ll sum = 0;
11         for(int j = 0; j < n; ++j){
12             sum = (sum + m[x][j] * m[y][(n+j-i)%n] % mod) % mod;
13         }
14         m[num][i] = sum;
15     }
16     return num;
17 }
18 int q_m(int x){
19     int a = 0, b = 1;
20     while(x){
21         if(x&1) a = mul(a, b);
22         b = mul(b, b);
23         x >>= 1;
24     }
25     return a;
26 }
27 int main(){
28     while(scanf("%d%d%d%d", &n, &mod, &d, &k) == 4){
29         num = 1;
30         for(int i = 0; i < n; ++i) scanf("%lld", a+i);
31         for(int i = 0; i < n; ++i){
32             m[0][i] = i == 0 ? 1 : 0;
33             m[1][i] = (i <= d || i >= n-d) ? 1 : 0;
34         }
35         int x = q_m(k);
36         for(int i = 0; i < n; ++i){
37             ll sum = 0;
38             for(int j = 0; j < n; ++j){
39                 sum = (sum + (a[j]*m[x][(n-i+j)%n])%mod) % mod;
40             }
41             if(i != n-1) printf("%lld ", sum);
42             else printf("%lld
", sum);
43         }
44     }
45     return 0;
46 }

--------------------------------------------------------------------------------------------------------------------

http://acm.hdu.edu.cn/showproblem.php?pid=2256

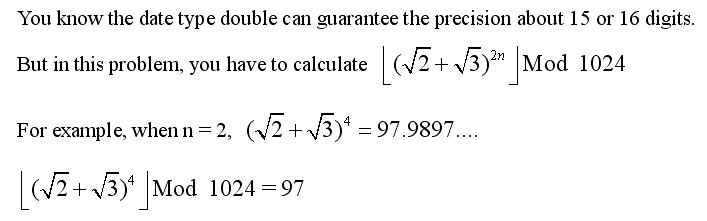
盗图

（/2 + /3）^2*n = = (5+2/6)^n;

(5+2/6)^n + (5-2/6)^n = 1

 1 #include <iostream>
 2 #include <cmath>
 3 using namespace std;
 4 struct Node{
 5     int x[2][2];
 6 };
 7 int n;
 8 const int MOD = 1024;
 9 Node mul(Node x, Node y){
10     Node X;
11     X.x[0][0] = X.x[0][1] = X.x[1][0] = X.x[1][1] = 0;
12     for(int i = 0; i < 2; ++i){
13         for(int j = 0; j < 2; ++j){
14             for(int k = 0; k < 2; ++k){
15                 X.x[i][j] = (X.x[i][j] + x.x[i][k]*y.x[k][j]%MOD)%MOD;
16             }
17         }
18     }
19     return X;
20 }
21 Node q_m(Node A, int x){
22     Node AA;
23     AA.x[0][0] = AA.x[1][1] = 1;
24     AA.x[0][1] = AA.x[1][0] = 0;
25     while(x){
26         if(x&1) AA = mul(AA, A);
27         A = mul(A, A);
28         x >>= 1;
29     }
30     return AA;
31 }
32 int main(){
33     int t;
34     scanf("%d", &t);
35     while(t--){
36         scanf("%d", &n);
37         Node A;
38         A.x[0][0] = A.x[1][1] = 5;
39         A.x[0][1] = 12, A.x[1][0] = 2;
40         Node AA = q_m(A, n);
41         //printf("%d
", (AA.x[0][0]+(int)floor((double)AA.x[1][0]*sqrt(6.0)))%MOD);
42         printf("%d
", (2*AA.x[0][0]-1)%MOD);
43     }
44     return 0;
45 }

--------------------------------------------------------------------------------------------------------------------

http://acm.hdu.edu.cn/showproblem.php?pid=4565

套路题

（X，Y，Z）|A| = （X', Y', Z'）

 1 #include <iostream>
 2 using namespace std;
 3 #define ll long long
 4 ll a, b, n, m;
 5 struct Node{
 6     ll x[2][2];
 7 };
 8 Node mul(Node xx, Node yy){
 9     Node AAA;
10     for(int i = 0; i < 2; ++i){
11         for(int j = 0; j < 2; ++j){
12             AAA.x[i][j] = 0;
13             for(int k = 0; k < 2; ++k){
14                 AAA.x[i][j] = (AAA.x[i][j] + xx.x[i][k]*yy.x[k][j]%m)%m;
15             }
16         }
17     }
18     return AAA;
19 }
20 Node q_m(Node A, int x){
21     Node AA;
22     AA.x[0][0] = AA.x[1][1] = 1;
23     AA.x[0][1] = AA.x[1][0] = 0;
24     while(x){
25         if(x&1) AA = mul(AA, A);
26         A = mul(A, A);
27         x >>= 1;
28     }
29     return AA;
30 }
31 int main(){
32     while(~scanf("%lld%lld%lld%lld", &a, &b, &n, &m)){
33         Node A;
34         A.x[0][0] = a, A.x[0][1] = 1;
35         A.x[1][0] = b, A.x[1][1] = a;
36         Node AA = q_m(A, n);
37         //cout<<AA.x[0][0]<<endl;
38         printf("%lld
", 2*(AA.x[0][0])%m);
39     }
40     return 0;
41 }

--------------------------------------------------------------------------------------------------------------------

http://acm.hdu.edu.cn/showproblem.php?pid=4291

矩阵幂次幂，，找循环节。。。。。。看别人的代码才相通的，还是自己太菜

 1 #include <iostream>
 2 using namespace std;
 3 #define ll long long
 4 ll Mod;
 5 ll Mo[3] = {183120LL, 222222224LL, 1000000007LL};
 6 ll a[3];
 7 ll call(ll x){
 8     a[0] = 0LL, a[1] = 1LL, a[2] = 3LL;
 9     for(ll i = 3LL; ;i++){
10         a[i%3] = (3LL*a[(i-1)%3]+a[(i-2)%3])%x;
11         if(a[i%3] == 3LL && a[(i-1)%3] == 1LL) return i-2;
12     }
13 }
14 ll n;
15 struct Node{
16     ll x[2][2];
17 };
18 Node mul(Node xx, Node yy){
19     Node AAA;
20     for(int i = 0; i < 2; ++i){
21         for(int j = 0; j < 2; ++j){
22             AAA.x[i][j] = 0;
23             for(int k = 0; k < 2; ++k){
24                 AAA.x[i][j] = (AAA.x[i][j] + xx.x[i][k]*yy.x[k][j]%Mod)%Mod;
25             }
26         }
27     }
28     return AAA;
29 }
30 ll q_m(ll x){
31     for(int i = 0; i < 3; ++i){
32         Mod = Mo[i];
33         Node AA, A;
34         AA.x[0][0] = AA.x[1][1] = 1;
35         AA.x[0][1] = AA.x[1][0] = 0;
36         A.x[0][0] = 3, A.x[0][1] = 1;
37         A.x[1][0] = 1, A.x[1][1] = 0;
38         while(x){
39             if(x&1) AA = mul(AA, A);
40             A = mul(A, A);
41             x >>= 1;
42         }
43         x = AA.x[0][0]-1;
44         if(x == -1) return 0;
45     }
46     return x+1;
47 }
48 int main(){
49     while(~scanf("%lld", &n)){
50         if(n == 0){
51             puts("0");
52             continue;
53         }
54         //Node AA = q_m(A, n-1);
55         //cout<<AA.x[0][0]<<endl;
56         printf("%lld
", q_m(n-1));
57         //cout<<call(Mod)<<endl;//222222224
58         //cout<<call(222222224LL)<<endl;//183120
59     }
60     return 0;
61 }

--------------------------------------------------------------------------------------------------------------------

http://poj.org/problem?id=3233

求矩阵一次方加到k次方对m取模

等差数列用二分

 1 #include <stdio.h>
 2 #include <iostream>
 3 #include <string.h>
 4 using namespace std;
 5 #define ll long long
 6 int n, k, m;
 7 struct Node{
 8     int x[31][31];
 9 }A;
10 Node Sum(Node a, Node b){
11     for(int i = 0; i < n; ++i){
12         for(int j = 0; j < n; ++j){
13             a.x[i][j] = (a.x[i][j] + b.x[i][j])%m;
14         }
15     }
16     return a;
17 }
18 Node mul(Node a, Node b){
19     Node B;
20     for(int i = 0; i < n; ++i){
21         for(int j = 0; j < n; ++j){
22             B.x[i][j] = 0;
23             for(int k = 0; k < n; ++k){
24                 B.x[i][j] = (B.x[i][j] + a.x[i][k]*b.x[k][j]%m)%m;
25             }
26         }
27     }
28     return B;
29 }
30 Node q_m(Node AAA, Node A, ll x){
31     while(x){
32         if(x&1) AAA = mul(AAA, A);
33         A = mul(A, A);
34         x >>= 1;
35     }
36     return AAA;
37 }
38 void solve(){
39     Node AA, AAA, X;
40     for(int i = 0; i < n; ++i){
41         for(int j = 0; j < n; ++j){
42             AA.x[i][j] = 0;
43             X.x[i][j] = AAA.x[i][j] = (i == j);
44         }
45     }
46     while(k > 1){
47         if(k&1){
48             AA = Sum(AA, mul(X, q_m(AAA, A, k))); //开始q_m没有乘X导致WA了好几次
49         }
50         k >>= 1;
51         X = mul(Sum(AAA, q_m(AAA, A, k)), X);
52     }
53     X = Sum(mul(A, X), AA);
54     for(int i = 0; i < n; ++i){
55         for(int j = 0; j < n; ++j){
56             printf("%d%c", X.x[i][j], (j == n-1 ? '
' : ' '));
57         }
58     }
59 }
60 int main(){
61     while(~scanf("%d%d%d", &n, &k, &m)){
62         for(int i = 0; i < n; ++i){
63             for(int j = 0; j < n; ++j){
64                 scanf("%d", &A.x[i][j]);
65             }
66         }
67         solve();
68     }
69     return 0;
70 }

构造矩阵，，woc，这也能构造？？？？，，，厉害了。。。。

设　　　　|A　A| 为X

　　　　　|0　I |

则

（I, 0） X = (A, A);　　(A, A) X = (A^2, A^2+A)........

 1 #include <iostream>
 2 #include <string.h>
 3 using namespace std;
 4 const int maxn = 62;
 5 int A[maxn][maxn], B[maxn][maxn];
 6 int n, k, m, x;
 7 void mul(int a[maxn][maxn], int b[maxn][maxn], int x){
 8     int y[maxn][maxn];
 9     for(int i = 0; i < x; ++i){
10         for(int j = 0; j < x; ++j){
11             y[i][j] = 0;
12             for(int k = 0; k < x; ++k){
13                 y[i][j] = (y[i][j] + a[i][k]*b[k][j]%m)%m;
14             }
15         }
16     }
17     memcpy(a, y, sizeof(y));
18 }
19 void q_m(int x, int xx){
20     for(int i = 0; i < x; ++i){
21         for(int j = 0; j < x; ++j){
22             B[i][j] = (i == j);
23         }
24     }
25     while(xx){
26         if(xx&1) mul(B, A, x);
27         mul(A, A, x);
28         xx >>= 1;
29     }
30     for(int i = 0; i < n; ++i){
31         for(int j = n; j < x; ++j){
32             printf("%d%c", B[i][j], (j == x-1 ? '
' : ' '));
33         }
34     }
35 }
36 int main(){
37     while(~scanf("%d%d%d", &n, &k, &m)){
38         memset(A, 0, sizeof(A));
39         for(int i = 0; i < n; ++i){
40             for(int j = 0; j < n; ++j){
41                 scanf("%d", &x);
42                 A[i][j] = A[i][n+j] = x;
43             }
44             A[i+n][i+n] = 1;
45         }
46         q_m(2*n, k);
47     }
48     return 0;
49 }

下面的代码是二分写的，上面是构造矩阵的。很明显，，构造的代码不但简单好写而且耗时短，比二分快了将近三倍。。。6666666

看来还是构造吊一点。。毕竟一次快速幂就可以出来，而二分的话要多次快速幂。。。。

--------------------------------------------------------------------------------------------------------------------

http://acm.hdu.edu.cn/showproblem.php?pid=5667

矩阵快速幂加费马定理

 1 #include <iostream>
 2 using namespace std;
 3 #define ll long long
 4 ll n, a, b, c, p, Mod;
 5 struct Node{
 6     ll x[3][3];
 7 };
 8 Node mul(Node a, Node b){
 9     Node B;
10     for(int i = 0; i < 3; ++i){
11         for(int j = 0; j < 3; ++j){
12             B.x[i][j] = 0;
13             for(int k = 0; k < 3; ++k){
14                 B.x[i][j] = (B.x[i][j] + a.x[i][k]*b.x[k][j]%Mod)%Mod;
15             }
16         }
17     }
18     return B;
19 }
20 ll Q_m(ll a, ll x){
21     if(a == 0) return 0;
22     ll X = 1LL;
23     while(x){
24         if(x&1) X = X*a%p;
25         a = a*a%p;
26         x >>= 1;
27     }
28     return X;
29 }
30 void q_m(){
31     Node A, AA;
32     Mod = p-1LL;
33     for(int i = 0; i < 3; ++i){
34         for(int j = 0; j < 3; ++j){
35             AA.x[i][j] = (i == j);
36             A.x[i][j] = 0LL;
37         }
38     }
39     A.x[1][1] = c%Mod;
40     A.x[1][0] = A.x[2][1] = A.x[0][1] = A.x[2][2] = 1LL;
41     n --;
42     while(n){
43         if(n&1) AA = mul(AA, A);
44         A = mul(A, A);
45         n >>= 1;
46     }
47     /*
48     for(int i = 0; i < 3; ++i){
49         for(int j = 0; j < 3; ++j){
50             printf("%lld%c", AA.x[i][j], (j == 2 ? '
' : ' '));
51         }
52     }
53     */
54     b%=Mod;
55     printf("%lld
", Q_m(a%p, ((AA.x[1][0]+AA.x[2][0])%Mod)*b%Mod));
56 }
57 int main(){
58     int t;
59     scanf("%d", &t);
60     while(t--){
61         scanf("%lld%lld%lld%lld%lld", &n, &a, &b, &c, &p);
62         q_m();
63     }
64     return 0;
65 }

--------------------------------------------------------------------------------------------------------------------

http://acm.hdu.edu.cn/showproblem.php?pid=5451

一个网络赛的题目，，，漩斌大神可是十分钟就A的题，。。。我太菜！！！！！！！！！

 1 #include <iostream>
 2 #include <stdio.h>
 3 #include <string.h>
 4 using namespace std;
 5 #define ll long long
 6 ll n, m, Mod;
 7 int a[50000];
 8 bool vis[50000];
 9 struct Node{
10     ll x[2][2];
11 };
12 int w = 1;
13 ll Q_m(){
14     ll X = 1LL, x = 2LL;
15     while(n){
16         if(n&1) X = X*x%Mod;
17         x = x*x%Mod;
18         n >>= 1;
19     }
20     return X;
21 }
22 Node mul(Node a, Node b){
23     Node B;
24     for(int i = 0; i < 2; ++i){
25         for(int j = 0; j < 2; ++j){
26             B.x[i][j] = 0;
27             for(int k = 0; k < 2; ++k){
28                 B.x[i][j] = (B.x[i][j] + a.x[i][k]*b.x[k][j]%Mod)%Mod;
29             }
30         }
31     }
32     return B;
33 }
34 ll get(Node A, Node AA){
35     for(ll i = 1; ; ++i){
36      //cout<<"*********"<<endl;
37         AA = mul(A, AA);
38         if(AA.x[0][0] == 5%Mod && AA.x[0][1] == 2%Mod && AA.x[1][0] == 12%Mod && AA.x[1][1] == 5%Mod){
39            // cout<<i<<"***************"<<endl;
40             return i;
41         }
42     }
43 }
44 void q_m(){
45     Node A, AA;
46     AA.x[0][0] = AA.x[1][1] = 1LL;
47     AA.x[1][0] = AA.x[0][1] = 0;
48     A.x[0][0] = A.x[1][1] = 5LL;
49     A.x[0][1] = 2LL, A.x[1][0] = 12LL;
50     if(!vis[m]){
51         Mod = m;
52         Mod = get(A, A);
53         vis[m] = true;
54         a[m] = Mod;
55     }else{
56         Mod = a[m];
57     }
58     ll x = Q_m()+1LL;
59     Mod = m;
60     while(x){
61         if(x&1) AA = mul(AA, A);
62         A = mul(A, A);
63         x >>= 1;
64     }
65     printf("Case #%d: %lld
", w++, (2LL*AA.x[0][0]%Mod-1LL+Mod)%Mod);
66 }
67 int main(){
68     int t;
69     scanf("%d", &t);
70     while(t--){
71         scanf("%lld%lld", &n, &m);
72         q_m();
73     }
74     return 0;
75 }

该题循环节为（m+1）*（m-1）

细节参考

关于斐波那契数列的循环节：http://blog.csdn.net/acdreamers/article/details/25616461

--------------------------------------------------------------------------------------------------------------------

中南邀请赛（湘潭） http://202.197.224.59/OnlineJudge2/index.php/Problem/read/id/1243

找循环节。。

挖了好次，有几个特例。。。。

  1 #include <iostream>
  2 #include <string.h>
  3 #include <stdio.h>
  4 using namespace std;
  5 #define ll long long
  6 struct Node{
  7     int x[2][2];
  8 };
  9 Node T, M;
 10 int Mod;
 11 char str[100009];
 12 Node mul(Node a, Node b){
 13     Node c;
 14     for(int i = 0; i < 2; ++i){
 15         for(int j = 0; j < 2; ++j){
 16             c.x[i][j] = 0;
 17             for(int k = 0; k < 2; ++k){
 18                 c.x[i][j] = (c.x[i][j] + a.x[i][k]*b.x[k][j]%7)%7;
 19             }
 20         }
 21     }
 22     return c;
 23 }
 24 void read(Node b){
 25     for(int i = 0; i < 2; ++i){
 26         for(int j = 0; j < 2; ++j){
 27             if(j == 1) printf("%d
", b.x[i][j]);
 28             else printf("%d ", b.x[i][j]);
 29         }
 30     }
 31 }
 32 bool go(){
 33     //read(T);
 34     for(int i = 2; ; ++i){
 35         //cout<<"&&"<<endl;
 36         M = mul(T, M);
 37         if(!M.x[0][0] && !M.x[0][1] && !M.x[1][0] &&!M.x[1][1]){
 38             //read(T);
 39             //printf("%d******
", i);
 40             return false;
 41         }
 42         if(M.x[0][0] == T.x[0][0] && M.x[0][1] == T.x[0][1] && M.x[1][0] == T.x[1][0] && M.x[1][1] == T.x[1][1]){
 43             Mod = i - 1;
 44             //printf("%d%%%%
", i);
 45             return true;
 46         }
 47     }
 48 }
 49 void q(Node a, ll x){
 50     Node b;
 51     b.x[0][0] = b.x[1][1] = 1;
 52     b.x[0][1] = b.x[1][0] = 0;
 53     while(x){
 54         if(x&1) b = mul(b, a);
 55         a = mul(a, a);
 56         x >>= 1;
 57     }
 58     read(b);
 59 }
 60 
 61 void lala(int x){
 62     if(x == 4){
 63         M.x[0][0] = T.x[0][0], M.x[0][1] = T.x[0][1];
 64         M.x[1][0] = T.x[1][0], M.x[1][1] = T.x[1][1];
 65         go();
 66         return ;
 67     }
 68     for(int i = 0; i < 7; ++i){
 69         //cout<<i<<"**"<<x<<endl;
 70         T.x[x/2][x%2] = i;
 71         lala(x+1);
 72     }
 73 }
 74 
 75 int main(){
 76     //lala(0);
 77     while(~scanf(" %s", str)){
 78         int x, y, z, w;
 79         scanf("%d%d%d%d", &x, &y, &z, &w);
 80         T.x[0][0] = M.x[0][0] = x, T.x[0][1] = M.x[0][1] = y;
 81         T.x[1][0] = M.x[1][0] = z, T.x[1][1] = M.x[1][1] = w;
 82         int len = strlen(str);
 83         if(!go()){
 84             if(len == 1 && str[0] == '1') printf("%d %d
%d %d
", x, y, z, w);
 85             else printf("0 0
0 0
");
 86             continue;
 87         }
 88         //printf("%d****
", Mod);
 89         if(Mod == 1){
 90             printf("%d %d
%d %d
", x, y, z, w);
 91             continue;
 92         }
 93         ll sum = 0;
 94         for(int i = 0; i < len; ++i){
 95             //cout<<sum<<" "<<i<<endl;
 96             sum = (sum*10+str[i]-'0')%Mod;
 97         }
 98         //cout<<sum<<endl;
 99         q(T, sum);
100     }
101     return 0;
102 }

--------------------------------------------------------------------------------------------------------------------

只有不断学习才能进步！

查看全文

相关阅读:
java打包成windows服务（转）
java程序在windows系统作为服务程序运行(转)
java String 转 Long 两种方法区别(转)
css清除浮动clearfix:after的用法详解(转)
管理界面的头2
ROS 设置串口USB软连接
 ROS 用 roboware实现节点信息发送和接收
 javascript实现html中关键字查询
 winfrom 中 label 文字随着窗体大小变化
 lattice planner 规划详解

原文地址：https://www.cnblogs.com/wenbao/p/6506556.html