#include<stdio.h>
#include<stdlib.h>
int array[15][15];
int init(int degree) //初始化
{
int i;
int j;
for(i=0; i<=degree+1; i++)
for(j=0; j<=degree+1; j++)
array[i][j] = 0;
return 0;
}
int test_print(int x, int y, int w, int h) //测试用的,输出以(x,y)为原点,宽为w,高为h,这个区域的数值
{
int i;
int j;
for(i=y; i<=y+h-1; i++){
for(j=x; j<=x+w-1; j++){
printf("%2d ",array[i][j]);
}
printf("
");
}
return 0;
}
int lao_bo_er(int degree, int x, int y, int num) //劳伯法
{
int i;
int j;
int k;
i = y;
j = degree/2 + x;
for(k=num; k<=num+degree*degree-1; k++){
array[i][j] = k;
if((k-num+1)%degree == 0){ //如果这个数所要放的格已经有数填入
i = (i-y+1)%degree+y;
}
else{ //每一个数放在前一个数的右上一格
i = (i-y-1+degree)%degree+y;
j = (j-x+1)%degree+x;
}
}
return 0;
}
int seq_range(int degree) //把数字按顺序填
{
int i;
int j;
int num;
num = 1;
for(i=1; i<=degree; i++){
for(j=1; j<=degree; j++){
array[i][j] = num++;
}
}
return 0;
}
int si_te_la_zi(int degree, int x, int y, int num) //斯特拉兹法
{
int deg;
int k;
int temp;
int i;
int j;
deg = degree/2;
lao_bo_er(deg, x, y, num); //用罗伯法,依次在A象限,D象限,B象限,C象限按奇数阶幻方的填法填数
lao_bo_er(deg, x+deg, y, num+2*deg*deg);
lao_bo_er(deg, x, y+deg, num+3*deg*deg);
lao_bo_er(deg, x+deg, y+deg, num+deg*deg);
k = (degree-2)/4;
for(i=1; i<=deg; i++){ //A象限和C象限对换数据
for(j=1; j<=k; j++){
temp = array[i][j];
array[i][j] = array[i+deg][j];
array[i+deg][j]=temp;
}
for(j=deg+deg/2+1; j>=deg+deg/2-k+3; j--){
temp = array[i][j];
array[i][j] = array[i+deg][j];
array[i+deg][j]=temp;
}
}
for(i=j=1; j<=deg/2+k; j++){ //B象限和D象限对换数据
temp = array[i+deg/2][j];
array[i+deg/2][j] = array[i+deg+deg/2][j];
array[i+deg+deg/2][j]=temp;
}
return 0;
}
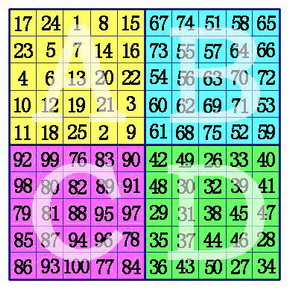
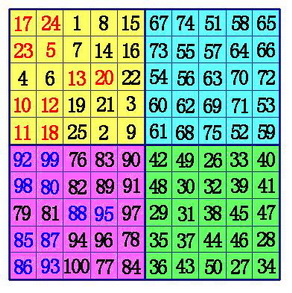
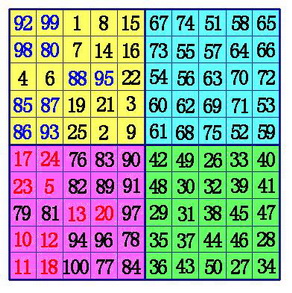
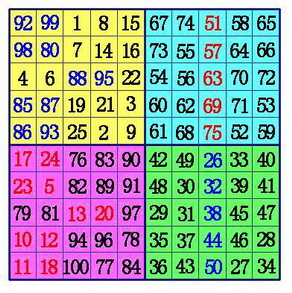
int hai_er_fa(int degree) //海尔法
{
int i;
int j;
int complement;
int deg;
seq_range(degree);
complement = degree*degree+1;
deg = degree/4;
for(i=0; i<deg; i++){
for(j=0; j<deg; j++){ //对角线上的数字换成和它互补的数
array[i*4+1][j*4+1] = complement - array[i*4+1][j*4+1];
array[i*4+1][j*4+4] = complement - array[i*4+1][j*4+4];
array[i*4+4][j*4+1] = complement - array[i*4+4][j*4+1];
array[i*4+4][j*4+4] = complement - array[i*4+4][j*4+4];
array[i*4+2][j*4+2] = complement - array[i*4+2][j*4+2];
array[i*4+2][j*4+3] = complement - array[i*4+2][j*4+3];
array[i*4+3][j*4+2] = complement - array[i*4+3][j*4+2];
array[i*4+3][j*4+3] = complement - array[i*4+3][j*4+3];
}
}
return 0;
}
int main()
{
int degree;
printf("please input the degree
");
scanf("%d",°ree);
init(degree);
if(degree%2 == 1){ //奇数阶幻方
lao_bo_er(degree,1,1,1);
test_print(1,1,degree,degree);
}
else if(degree%4 == 2){ //双偶阶幻方
si_te_la_zi(degree, 1, 1, 1);
test_print(1,1,degree,degree);
}
else{ //单偶阶幻方
hai_er_fa(degree);
test_print(1,1,degree,degree);
}
return 0;
}