NET与Matlab结合 —— 最小二乘法直线拟合（C#） 首先是一个.m文件drawgraph.m，确保它能够在Matlab里运行。
我这里是最小二乘法直线拟合程序。
%最小二乘法直线拟合
%Created by Safirst C. Ke 2007.8.29 Wed 14:51
function drawgraph(coords)
%传入的参数为两行向量，第一行为x坐标，第二行为坐标。
%axis ([0 100 0 100]);
grid on;
hold on;
%显示欲拟合的点的位置
plot(coords(1,:), coords(2,:), '*');
%分解x，y坐标
x = coords(1,:)
y = coords(2,:)'
b = size(coords);
c = ones(1, b(2));
MT = [c; x];
M = MT';
%f为直线函数，f = mx + b;
f = inv(MT * M) * MT * y
['y = ', num2str(f(2)), 'x + ', num2str(f(1))]
%显示最终拟合的直线
x = -max(x):max(x);
y = f(1) + f(2) * x;
plot(x, y);
xlabel('X轴');
ylabel('Y轴');
title('最小二乘法直线拟合 by Safirst C. Ke');
legend(['y = ', num2str(f(2)), 'x + ', num2str(f(1))]);
然后将这个文件包含在.NET的类库工程中，并进行编译。
这里需要理解它的过程，毕竟.NET不能编译.m文件。怎么做到的呢？
通过设置这个工程的生成事件属性，添加为
call PlotDemoBuild.bat
然后在PlotDemoBuild.bat这个文件里面写好用Matlab编译器mcc编译的命令行，最重要的部分就是
mcc -M -silentsetup -vg -B "dotnet:PlotDemoComp,Plotter,2.0,private" -d ../../src ../../drawgraph.m
这样的话，点击生成，就会通过mcc产生dll，即我们需要的类库。
然后建立我们真正的C#工程，添加引用为刚才的类库，并开始写程序program.cs
using System;
using System.Collections.Generic;
using System.Text;
using MathWorks.MATLAB.NET.Utility;
using MathWorks.MATLAB.NET.Arrays;
//这两个引用显然要添加，不过好在这两个命名空间属于一个库MWArray.dll
//C:/Program Files/MATLAB/R2007a/toolbox/dotnetbuilder/bin/win32/v2.0/MWArray.dll
using PlotDemoComp;
namespace ConsoleApplication2
{
class Program
{
//[STAThread]
static void Main(string[] args)
{
try
{
Console.WriteLine("Please Input the points you want to fit:");
string[] y = Console.ReadLine().Trim().Split();
int size = y.Length;
double[] x = new double[size];
for(int i = 0; i < size; i++)
{
x[i] = Convert.ToDouble(y[i]);
}
double[,] pointValues = new double[2, size / 2];
//从开头算起，相邻的两个数为一个点，所以x和y都是间隔一个的。如1，2，3，4代表两点(1,2),(3,4)
for(int i = 0; i < size; i += 2)
{
int index = i / 2;
pointValues[0, index] = x[i];
}
for(int i = 1; i < size; i += 2)
{
int index = (i - 1) / 2;
pointValues[1, index] = x[i];
}
Plotter plotter = new Plotter();
plotter.drawgraph((MWNumericArray)pointValues);
Console.ReadLine();
}
catch(Exception exception)
{
Console.WriteLine("Error: {0}", exception);
}
}
}
}
运行结果如下：
Please Input the points you want to fit:
1 2 3 4 5 6 -1 -2 -3 -4 -5 -6
*号标记欲拟合的点，直线为拟合直线！
就写这么多，以后再加入一个曲线拟合的程序。
特别声明：在下学习.NET C#和Matlab的时间均不超过1个月，
望高手不要批评指责，照顾一下新手学习钻研的积极性！
假如给定的实验数据点为（Xi,Yi),其中i=0,1,...n,那么 直线与数据点的偏差平方和为
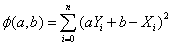
要使得
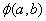取到极小值，则要求:
， 
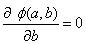这两个式子是取得极小值的必要条件，具体运算的过程如下:
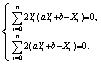
对该式求解得到:
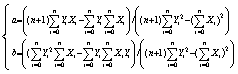
<!--[if !vml]--><!--[endif]-->
以下就是我用C#做的源代码:
{
/// <summary>
/// To Draw Linear Least Square Fitting Curve
/// </summary>
/// <param name="g">The device on which to draw the curve</param>
/// <param name="lp">A list of point used to do the approximation</param>
public static void LeastSquare2(Graphics g, List<PointF> lp)
{
// Clear the client window with the white color
g.Clear(Color.White);
// Move the drawing origin to the point(200,200)
g.TranslateTransform(200, 200);
// Use FillEllipse method to draw each point as an ellipse
foreach (PointF p in lp)
{
g.FillEllipse(Brushes.Red, new RectangleF(p.X - 5.0f, p.Y - 5.0f, 10.0f, 10.0f));
}
int i;
float a, b, sumX, sumY2, sumY, sumXY;
sumX = 0.0f;
sumY2 = 0.0f;
sumY = 0.0f;
sumXY = 0.0f;
// To calculate as per the description of the Mathematical Formular
for (i = 0; i < lp.Count; i++)
{
sumY += lp[i].Y;
sumY2 += lp[i].Y * lp[i].Y;
sumX += lp[i].X;
sumXY += lp[i].X * lp[i].Y;
}
// Deduct the coefficients required to do the approximation using the mathematical formular
a = (lp.Count * sumXY - sumX * sumY) / (lp.Count * sumY2 - sumY * sumY);
b = (sumY2 * sumX - sumY * sumXY) / (lp.Count * sumY2 - sumY * sumY);
Pen newPen = new Pen(Color.Blue, 3.0f);
g.DrawLine(newPen, new PointF(0, -b / a), new PointF(360, (360 - b) / a));
}
}
下面则是调用上述代码的程序:
{
// Declare a list of points
List<PointF> lp = new List<PointF>();
// PointF array
PointF[] pf = new PointF[]{
new PointF(0.0f,68.0f),
new PointF(10.0f,73.1f),new PointF(20.0f,66.4f),
new PointF(30.0f,70.6f),new PointF(40.0f,64.6f),
new PointF(50.0f,68.8f),new PointF(60.0f,61.0f),
new PointF(70.0f,65.8f),new PointF(80.0f,60.4f),
new PointF(90.0f,61.0f)
};
// Using AddRange method of the list to add the pointf array to the end of the list
lp.AddRange(pf);
// Call the static metod LeastSquare2 of LeastSquare Class to proceed
LeastSquare.LeastSquare2(this.CreateGraphics(), lp);
}
下面是本程序运行结果的屏幕截图(Screen Shot):