CF390-E. Inna and Large Sweet Matrix（区间更新＋区间查询）

题意很好理解，不说了

题解就是每次把值压缩成一维，比如x上，这样就可以求出任意宽度的整个竖条的和。

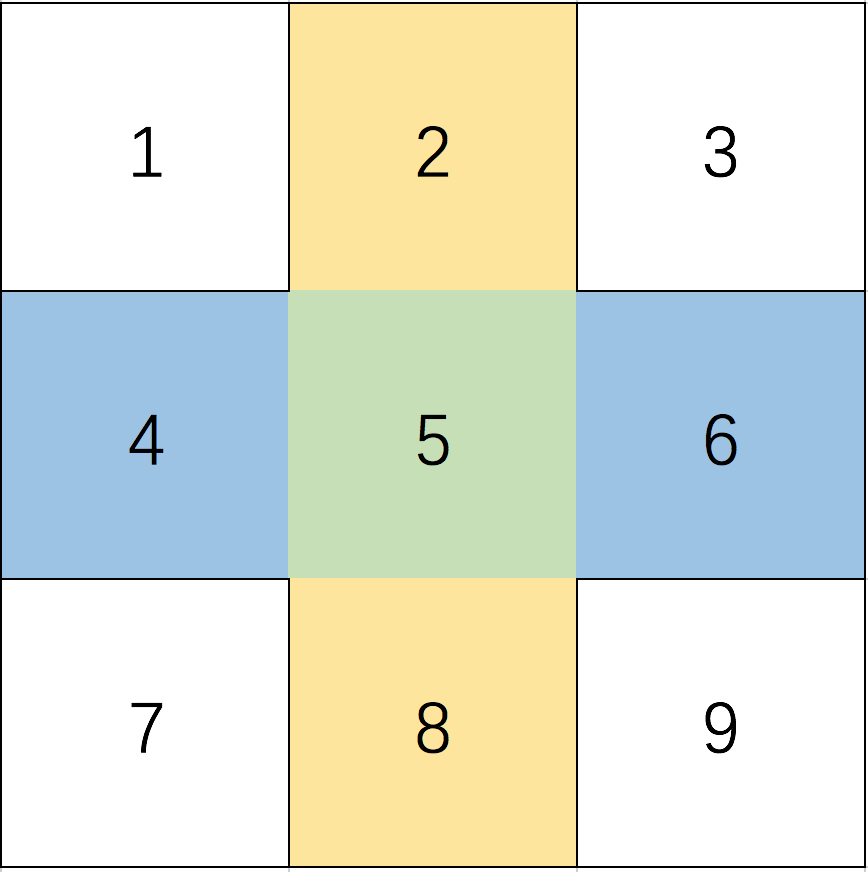
如这张图，求的是s5-(s1+s3+s7+s9)

因为可以求出一整竖条和一整横条，我们可以求出是s2+s5+s8 也可以求出s4+s5+s6 当然也很容易求出总面积S

那么S-(s2+s5+s8)-(s4+s5+s6) = s1+s3+s7+s9-s5

对，答案已经出来了，很简单。

以后看到这种求解公式十分奇怪的题，就要算一算是不是能构造出很简单的公式。

注意这题用cin cout 会超时！因为codeforce是单样例，所以都忘了这点，t了好多次……T^T

区间更新＋区间查询，线段树＋lazy操作 （514ms

#include <stdio.h>

typedef long long ll;

const int N = 4000005;
ll tx[N<<2], ty[N<<2], fx[N<<2], fy[N<<2];
int yl, yr, yv;
#define lson (o<<1)
#define rson ((o<<1)+1)

void pushdown(ll tr[], ll fg[], int o, int l, int r)
{
    if (fg[o]) {
        fg[lson] += fg[o];
        fg[rson] += fg[o];
        int m = (l+r) >> 1;
        tr[lson] += fg[o] * (m-l+1);
        tr[rson] += fg[o] * (r-m);
        fg[o] = 0;
    }
}

void add(ll tr[], ll fg[], int o, int l, int r)
{
    if (l == r) {
        tr[o] += yv;
        return ;
    }
    if (yl <= l && yr >= r) {
        tr[o] += (ll)yv * (r-l+1);
        fg[o] += yv;
        return ;
    }
    pushdown(tr, fg, o, l, r);
    int m = (l+r) >> 1;
    if (yl <= m) add(tr, fg, lson, l, m);
    if (yr > m) add(tr, fg, rson, m+1, r);
    tr[o] = tr[lson] + tr[rson];
}

ll query(ll tr[], ll fg[], int o, int l, int r)
{
    if (l >= yl && r <= yr) {
        return tr[o];
    }
    pushdown(tr, fg, o, l, r);
    int m = (l+r) >> 1;
    ll ans = 0;
    if (m >= yl) ans += query(tr, fg, o<<1, l, m);
    if (m < yr) ans += query(tr, fg, (o<<1)+1, m+1, r);
    return ans;
}


int main()
{

    int n, m, w;
    scanf("%d%d%d", &n, &m, &w);
    int op;
    int x1, x2, y1, y2;
    ll v;
    ll tot, ans;
    while (w--) {
        scanf("%d%d%d%d%d", &op, &x1, &y1, &x2, &y2);
        if (op) {
            yl = 1, yr = n;
            tot = query(tx, fx, 1, 1, n);
            ans = 0;
            yl = x1, yr = x2;
            ans += query(tx, fx, 1, 1, n);
            yl = y1, yr = y2;
            ans += query(ty, fy, 1, 1, m);
            printf("%lld
", ans-tot);
        } else {
            scanf("%lld", &v);
            yl = x1, yr = x2, yv = v*(y2-y1+1);
            add(tx, fx, 1, 1, n);
            yl = y1, yr = y2, yv = v*(x2-x1+1);
            add(ty, fy, 1, 1, m);
        }
    }
    return 0;
}

顺便学习了一下树状数组的区间操作（202ms 时间空间都优于线段树

#include <stdio.h>

typedef long long ll;

const int MAXN = 4000005;

int lowbit(int x) { return x&-x; }

struct tree_array {
    struct tree_array_single {
        int N; 
        ll arr[MAXN];
        void add(int x, ll v) { while(x <= N) arr[x] += v, x += lowbit(x); }  
        ll sum(int x) { ll sum = 0; while(x) sum+=arr[x], x-=lowbit(x); return sum; }  
    } T1, T2;  
    void add(int x, ll v) { T1.add(x, v); T2.add(x, x*v); }
    void update(int L, int R, ll v) { add(L, v); add(R+1, -v); }
    ll sum(int x) { return (x+1)*T1.sum(x)-T2.sum(x); }
    ll query(int L,int R) { return sum(R)-sum(L-1); }
} tx, ty;

int main()
{
    //freopen("in.txt", "r", stdin);
    int n, m, w;
    scanf("%d%d%d", &n, &m, &w);
    int op;
    int x1, x2, y1, y2;
    ll v;
    tx.T1.N = tx.T2.N = n;
    ty.T1.N = ty.T2.N = m;
    ll tot = 0;
    while (w--) {
        scanf("%d%d%d%d%d", &op, &x1, &y1, &x2, &y2);
        if (op) {
            ll ans = tx.query(x1, x2) + ty.query(y1, y2);
            printf("%lld
", ans-tot);
        } else {
            scanf("%lld", &v);
            tot += (y2-y1+1)*(x2-x1+1)*v;
            tx.update(x1, x2, v*(y2-y1+1));
            ty.update(y1, y2, v*(x2-x1+1));
        }
    }
    return 0;
}