快速幂小结

（本文不涉及取模运算……）

快速幂，顾名思义，就是快速地求幂运算。

现在要求x=yⁿ的值，最朴素的解法：

int pow(int y, int n) {
    int result = 1;
    for (int i = 0; i < n; i++) {
        result *= y;
    }
    return result;
}

x=pow(y,n)

复杂度是O(n)

当n是偶数的时候，我们设n=2*m，则x=yⁿ=y^2*m=(y^m)^2

当n是奇数的时候，我们设n=2*m+1，则x=yⁿ=y^2*m+1=y*(y^m)^2

这样，我们就把复杂度从O(n)降到了O(n/2)，递归下去，算法的复杂度就是O(log₂n)……该怎么解释这个……其实我不会……

用递归实现比较容易理解，具体代码：

int quick_pow(int y, int n) {
    if (n == 0) return 1;
    if (n % 2 == 1) {
        // n是奇数 n=2*m+1
        // x = y^(2*m+1) = y * (y^m)^2
        int m = n / 2;
        int temp = quick_pow(y, m);
        return y * temp *temp;
    } else {
        // n是偶数 n=2*m
        // x = y^(2*m) = (y^m)^2
        int m = n / 2;
        int temp = quick_pow(y, m);
        return temp *temp;
    }
}

可以简化一下~~

int quick_pow(int y, int n) {
    if (!n) return 1;
    int temp = quick_pow(y, n >> 1);
    if (n & 1) return y * temp *temp;
    else return temp *temp;
}

非递归的版本也很容易理解啦

int quick_pow(int y, int n) {
    int result = 1;
    while (n > 0) {
        if (n % 2 == 1) {
            // y^n = y^(2*m+1) = y*(y^2)^m
            result *= y;
            // 接下来让y=y^2, n=m
            y = y * y;
            n = n / 2;
        } else {
            // y^n = y^(2*m) = (y^2)^m
            y = y * y;
            n = n / 2;
        }
    }
    return result;
}

简化一下~~~

int quick_pow(int y, int n) {
    int result = 1;
    while (n) {
        if (n & 1) result *= y;
        y = y * y;
        n >>= 1;
    }
    return result;
}

矩阵快速幂

我们都知道斐波那契数列（Fibonacci sequence），1、1、2、3、5、8、13、21、34……每一项是前两项的和。

如果要求第n项，需要从第一项开始递推。

int fibonacci(int n) {
    int a[n];
    a[0] = 1, a[1] = 1;
    for (int i = 2; i < n; i++) {
        a[i] = a[i-1] + a[i-2];
    }
    return a[n-1];
}

复杂度很容易看出来，O(n)。

我们都是学过线性代数的人，那么也就知道矩阵。这里斐波那契数列可以通过矩阵来算。

首先复习一下矩阵乘法的公式

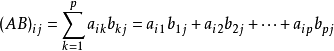
就是当我们求第 i 行第 j 列时，就使用第一个矩阵的第 i 行每一个元素和第二个矩阵第 j 列每一个元素分别相乘然后求和。所以第一个矩阵的列数要等于第二个矩阵的行数。

随便画一幅图理解下，

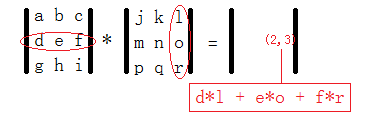
矩阵是怎么作用到这里的呢，我们设斐波那契数列为一个数组a[]，那么a[0]=1，a[1]=1，a[n]=a[n-1]+a[n-2]

通过这个递推公式，我们可以得出

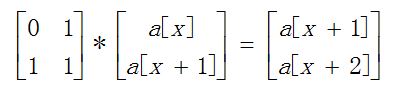
例如，

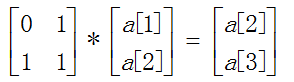
我们知道矩阵乘法满足结合律，接下来我们可以得出

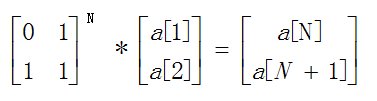
设构造的矩阵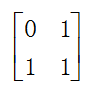为F

于是我们求a[n]的重点变成了求矩阵F的n次幂，此处可以直接将上文所述快速幂应用到这里。

注意构造的矩阵F必须是方阵，也就是行列必须相等，矩阵乘法的复杂度是O(k^3)，k是矩阵的行数。所以总复杂度就是O(log₂n*k^3)，因为一般k都非常小，所以总体复杂度大大降低。

矩阵乘法的代码比较简单，不想写了。。。。（才不说是忘了怎么写了。。

这样我们可以用矩阵快速求出所有类似的递推数列的第n项。

比如：a[n] =a[n-1]+a[n-3]+a[n-4]

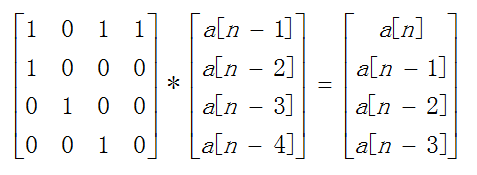
还是斐波那契数列，如果我们想求前n项的和，a[1]+a[2]+……+a[n]，依然可以通过矩阵快速幂求得、需求要简单的加一行用来记录当前和，

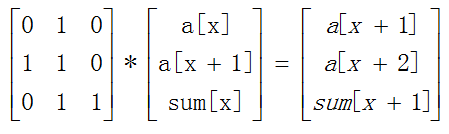
这样，

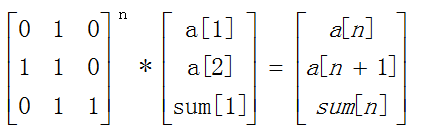
是不是好厉害，好神奇！

例题，如果你一次可以走1~k个楼梯，那么你要走到第n个楼梯有多少种走法？(k<n)

dp[n] = dp[n-1]+dp[n-2]+...+dp[n-k]

然后写出转移矩阵，快速幂求解即可。

例题 HDU5863

有k种不同的字符，每种字符有无限个，要求用这k种字符构造两个长度为n的字符串a和b，使得a串和b串的一一对应的连续相同字符长度不大于m，求方案数。

待续。。