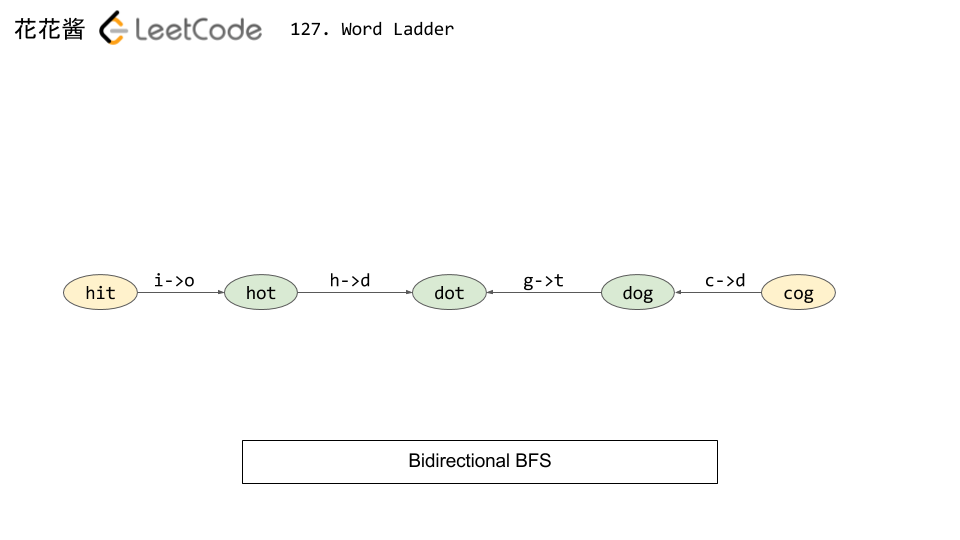
Given two words (beginWord and endWord), and a dictionary's word list, find the length of shortest transformation sequence from beginWord to endWord, such that:
- Only one letter can be changed at a time.
- Each transformed word must exist in the word list. Note that beginWord is not a transformed word.
Note:
- Return 0 if there is no such transformation sequence.
- All words have the same length.
- All words contain only lowercase alphabetic characters.
- You may assume no duplicates in the word list.
- You may assume beginWord and endWord are non-empty and are not the same.
Example 1:
Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"] Output: 5 Explanation: As one shortest transformation is "hit" -> "hot" -> "dot" -> "dog" -> "cog", return its length 5.
Example 2:
Input: beginWord = "hit" endWord = "cog" wordList = ["hot","dot","dog","lot","log"] Output: 0 Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.
// Author: Huahua // Running time: 92 ms (<76.61%) class Solution { public int ladderLength(String beginWord, String endWord, List<String> wordList) { Set<String> dict = new HashSet<>(); for (String word : wordList) dict.add(word); if (!dict.contains(endWord)) return 0; //不存在dict的endword直接返回0 Queue<String> q = new ArrayDeque<>(); q.offer(beginWord); int l = beginWord.length(); int steps = 0; while (!q.isEmpty()) { ++steps;//进入新的一层 for (int s = q.size(); s > 0; --s) { String w = q.poll(); char[] chs = w.toCharArray(); //方便修改某一位 for (int i = 0; i < l; ++i) { char ch = chs[i]; for (char c = 'a'; c <= 'z'; ++c) { if (c == ch) continue; //c == ch,重复,可以跳过 chs[i] = c; String t = new String(chs); if (t.equals(endWord)) return steps + 1; if (!dict.contains(t)) continue; //跳过无意义的case dict.remove(t); //dict单词只能使用一次,否则路径一定会增加 q.offer(t); } chs[i] = ch; //一位字符用完后要恢复原值 } } } return 0; } }
转自花花酱https://zxi.mytechroad.com/blog/searching/127-word-ladder/
https://www.youtube.com/watch?v=vWPCm69MSfs