310. Minimum Height Trees

For an undirected graph with tree characteristics, we can choose any node as the root. The result graph is then a rooted tree. Among all possible rooted trees, those with minimum height are called minimum height trees (MHTs). Given such a graph, write a function to find all the MHTs and return a list of their root labels.

Format
The graph contains n nodes which are labeled from 0 to n - 1. You will be given the number n and a list of undirected edges (each edge is a pair of labels).

You can assume that no duplicate edges will appear in edges. Since all edges are undirected, [0, 1] is the same as [1, 0] and thus will not appear together in edges.

Example 1 :

Input: n = 4, edges = [[1, 0], [1, 2], [1, 3]]

        0
        |
        1
       / 
      2   3 

Output: [1]

Example 2 :

Input: n = 6, edges = [[0, 3], [1, 3], [2, 3], [4, 3], [5, 4]]

     0  1  2
       | /
        3
        |
        4
        |
        5 

Output: [3, 4]

Note:

• According to the definition of tree on Wikipedia: “a tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.”
• The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

class Solution {
    public List<Integer> findMinHeightTrees(int n, int[][] edges) {
        if(n == 1) return Collections.singletonList(0);
        List<Integer>[] g = new ArrayList[n];
        
        for(int i = 0; i < n; i++) g[i] = new ArrayList();
        for(int[] e: edges){
            g[e[0]].add(e[1]);
            g[e[1]].add(e[0]);
        }
        List<Integer> leaves = new ArrayList();
        for(int i = 0; i < n; i++){
            if(g[i].size() == 1) leaves.add(i);
        }
        while(n > 2){
            n -= leaves.size();
            List<Integer> newleaves = new ArrayList();
            for(int i: leaves){
                int j = g[i].get(0);
                g[j].remove((Integer) i);
                if(g[j].size() == 1) newleaves.add(j);
            }
            leaves = newleaves;
        }
        return leaves;
    }
}

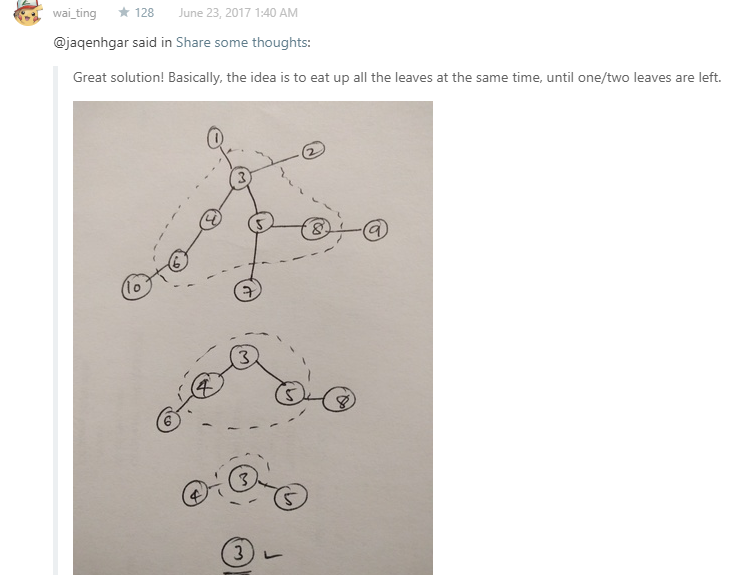
 每次把leaves（只有1个邻居）踢掉，最后剩下1或2个就是答案。

具体做法是先用arraylist数组存图，然后把leaves存起来，

进入循环后通过前一个leaves数组遍历找到他们相连的其他潜在leaves,通过remove除掉前一个leaves，判断是否成为了新的leaves并存到newleaves中，完事leaves = newleaves
为什么是n > 2呢？

因为是图，不存在circle，那说明最多有两个点能当根（偶数n），一个点当根（奇数n）。或者想想n个点，只有它的根在中点时，height才能minimum

class Solution {
    public List<Integer> findMinHeightTrees(int n, int[][] edges) {
        if(n == 1) return Collections.singletonList(0);
        Set<Integer>[] g = new HashSet[n];
        
        for(int i = 0; i < n; i++) g[i] = new HashSet();
        for(int[] e: edges){
            g[e[0]].add(e[1]);
            g[e[1]].add(e[0]);
        }
        List<Integer> leaves = new ArrayList();
        for(int i = 0; i < n; i++){
            if(g[i].size() == 1) leaves.add(i);
        }
        while(n > 2){
            n -= leaves.size();
            List<Integer> newleaves = new ArrayList();
            for(int i: leaves){
                int j = g[i].iterator().next();
                g[j].remove(i);
                if(g[j].size() == 1) newleaves.add(j);
            }
            leaves = newleaves;
        }
        return leaves;
    }
}

将arraylist替换成hashset能提高运算速度