You are given two sorted arrays of distinct integers nums1 and nums2.
A valid path is defined as follows:
- Choose array nums1 or nums2 to traverse (from index-0).
- Traverse the current array from left to right.
- If you are reading any value that is present in
nums1andnums2you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
Score is defined as the sum of uniques values in a valid path.
Return the maximum score you can obtain of all possible valid paths.
Since the answer may be too large, return it modulo 10^9 + 7.
Example 1:
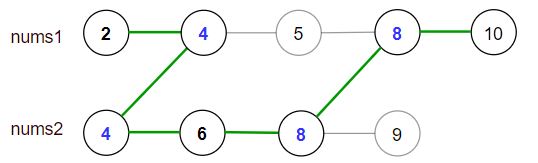
Input: nums1 = [2,4,5,8,10], nums2 = [4,6,8,9] Output: 30 Explanation: Valid paths: [2,4,5,8,10], [2,4,5,8,9], [2,4,6,8,9], [2,4,6,8,10], (starting from nums1) [4,6,8,9], [4,5,8,10], [4,5,8,9], [4,6,8,10] (starting from nums2) The maximum is obtained with the path in green [2,4,6,8,10].
Example 2:
Input: nums1 = [1,3,5,7,9], nums2 = [3,5,100] Output: 109 Explanation: Maximum sum is obtained with the path [1,3,5,100].
Example 3:
Input: nums1 = [1,2,3,4,5], nums2 = [6,7,8,9,10] Output: 40 Explanation: There are no common elements between nums1 and nums2. Maximum sum is obtained with the path [6,7,8,9,10].
Example 4:
Input: nums1 = [1,4,5,8,9,11,19], nums2 = [2,3,4,11,12] Output: 61
Constraints:
1 <= nums1.length <= 10^51 <= nums2.length <= 10^51 <= nums1[i], nums2[i] <= 10^7nums1andnums2are strictly increasing.
class Solution { public int maxSum(int[] nums1, int[] nums2) { int n1 = nums1.length, n2 = nums2.length; int i = 0, j = 0; long a = 0, b = 0; while(i < n1 || j < n2) { if(i < n1 && j < n2 && nums1[i] == nums2[j]) { a = b = Math.max(a, b) + nums1[i]; i++; j++; } else if(i < n1 && (j == n2 || nums1[i] < nums2[j])) { a += nums1[i++]; } else b += nums2[j++]; } return (int) (Math.max(a, b) % 1000000007); } }
https://zxi.mytechroad.com/blog/two-pointers/leetcode-1537-get-the-maximum-score/
2pointers DP
a是以nums1为结尾的最大path,b是nums2的
因为只有相同的时候才能跑过来,所以不同的时候只能老老实实走自己的路,每次把较小的往前挪动一位,否则会漏掉许多
如果nums1和nums2相同,说明面临选择,选择a和b中间大的加上当前值,把a、b重置成当前大值。