1557. Minimum Number of Vertices to Reach All Nodes

Given a directed acyclic graph, with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [fromi, toi] represents a directed edge from node fromi to node toi.

Find the smallest set of vertices from which all nodes in the graph are reachable. It's guaranteed that a unique solution exists.

Notice that you can return the vertices in any order.

Example 1:

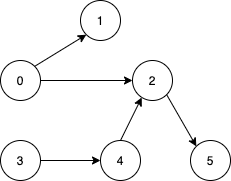
Input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
Output: [0,3]
Explanation: It's not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].

Example 2:

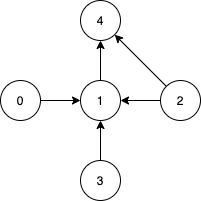
Input: n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
Output: [0,2,3]
Explanation: Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.

Constraints:

• 2 <= n <= 10^5
• 1 <= edges.length <= min(10^5, n * (n - 1) / 2)
• edges[i].length == 2
• 0 <= fromi, toi < n
• All pairs (fromi, toi) are distinct.

老union find了，回顾一下，unionfind是一个算法/数据结构，用来查找某个节点的祖先，以及把两个节点关联（union）起来。最后把所有独立的祖先找出来

这题和547 friend cycle有点像

class Solution {
    public List<Integer> findSmallestSetOfVertices(int n, List<List<Integer>> edges) {
        Set<Integer> set = new HashSet();
        boolean[] hasparent = new boolean[n];
        int[] anc = new int[n];
        for(int i = 0; i < n; i++) anc[i] = i;
        for(List<Integer> list : edges) {
            if(!hasparent[list.get(1)]) {
                union(list.get(1), list.get(0), anc);
                hasparent[list.get(1)] = true;
            }
            
        }
        for(int i = 0; i < n; i++) {
            set.add(find(anc, i));
        }
        return new ArrayList(set);
    }
    
    public int find(int[] anc, int x) {
        if(x != anc[x]) anc[x] = find(anc, anc[x]);
        return anc[x];
    }
    
    public void union(int x, int y, int[] anc) {
        int a = anc[x];
        int b = anc[y];
        anc[a] = b;
    }
}

有点注意的是可能节点的parent不止一个，我们就先到先得吧，设置一个used数组。