题意
给你一个 (n*m) 的矩阵,你可以每次将其中一个数 (+1) 或 (-1) ,求多少次可以使矩阵每一行每一列为回文的.
若一个数列 ((a_1,a_2,a_3,dots,a_n)) 为回文, (forall a_i ,a_i = a_{n-i+1})
( exttt{Data Range:})
(1 leq n,m leq 100,a_i leq 10^9)
思路
我们注意到,要使每行每列都是回文的,就要使
(a_{i,j} = a_{i,m-j+1} = a_{n-i+1,j} = a_{n-i+1,m-j+1})
如图:
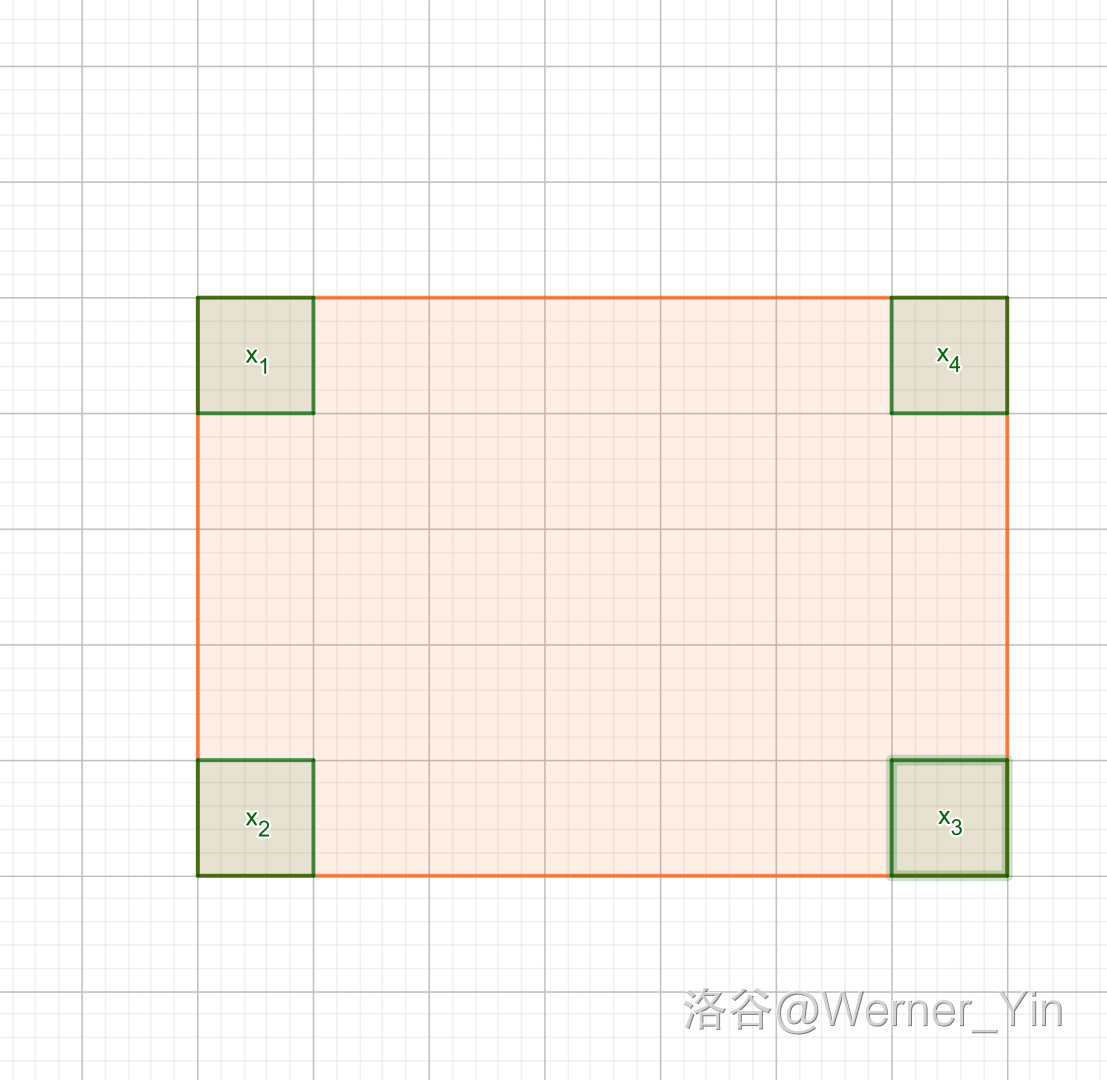
即图中的 (4) 个绿色方块
那我们只要每次处理这 (4) 个绿色方块,使其相同的操作次数最小。
设这 (4) 个方块的数从小到大为 (x_1,x_2,x_3,x_4) ,最后我们要是这些数都变为 (mid) 。
代价为 (s = |x_1-mid| + |x_2 - mid| + |x_3 - mid| + |x_4 - mid|)
结论
当 (x_2 leq mid leq x_3) , (s) 有最小值。
证明
如图:
绿色的线段和 代表 (s) 。
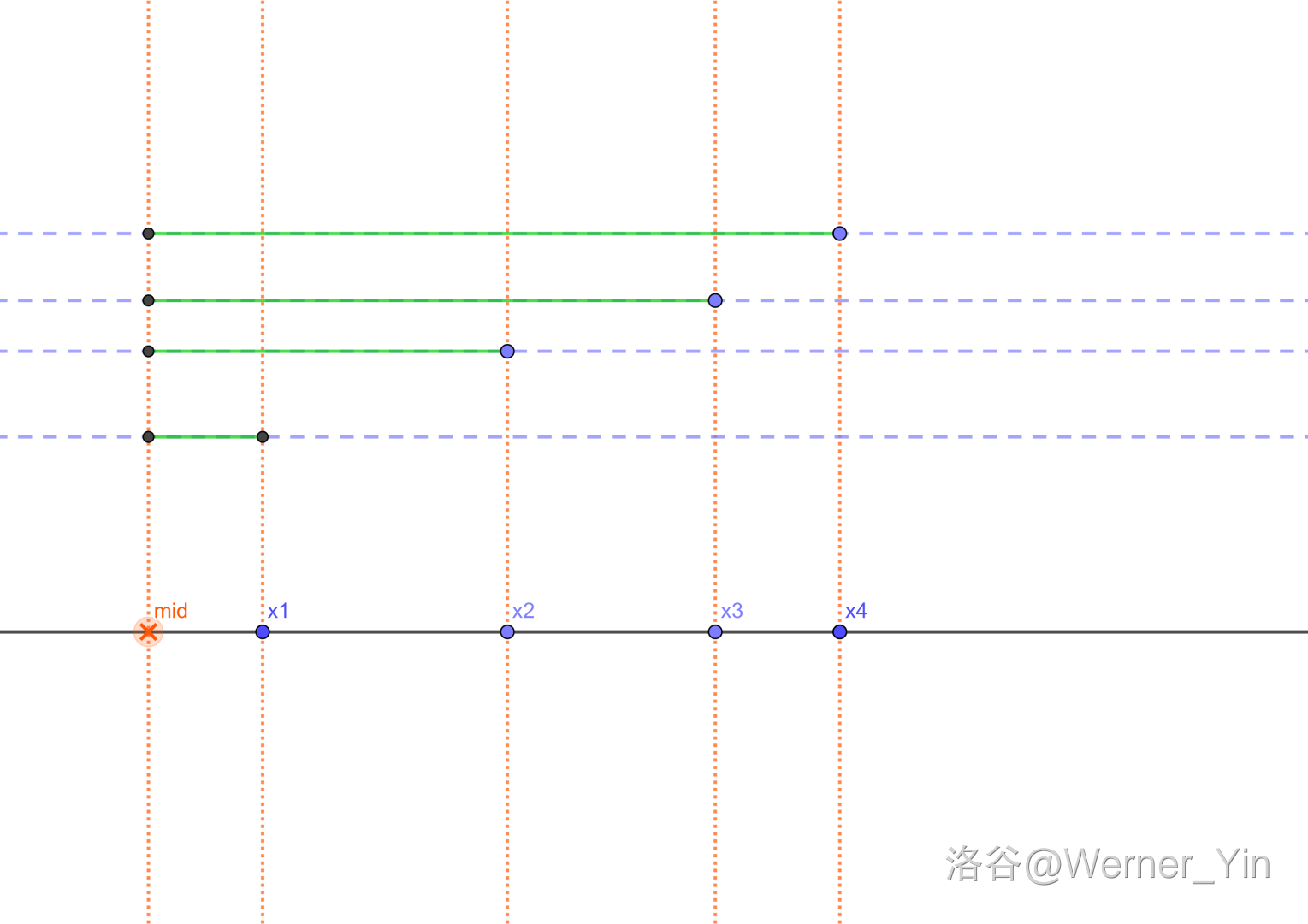
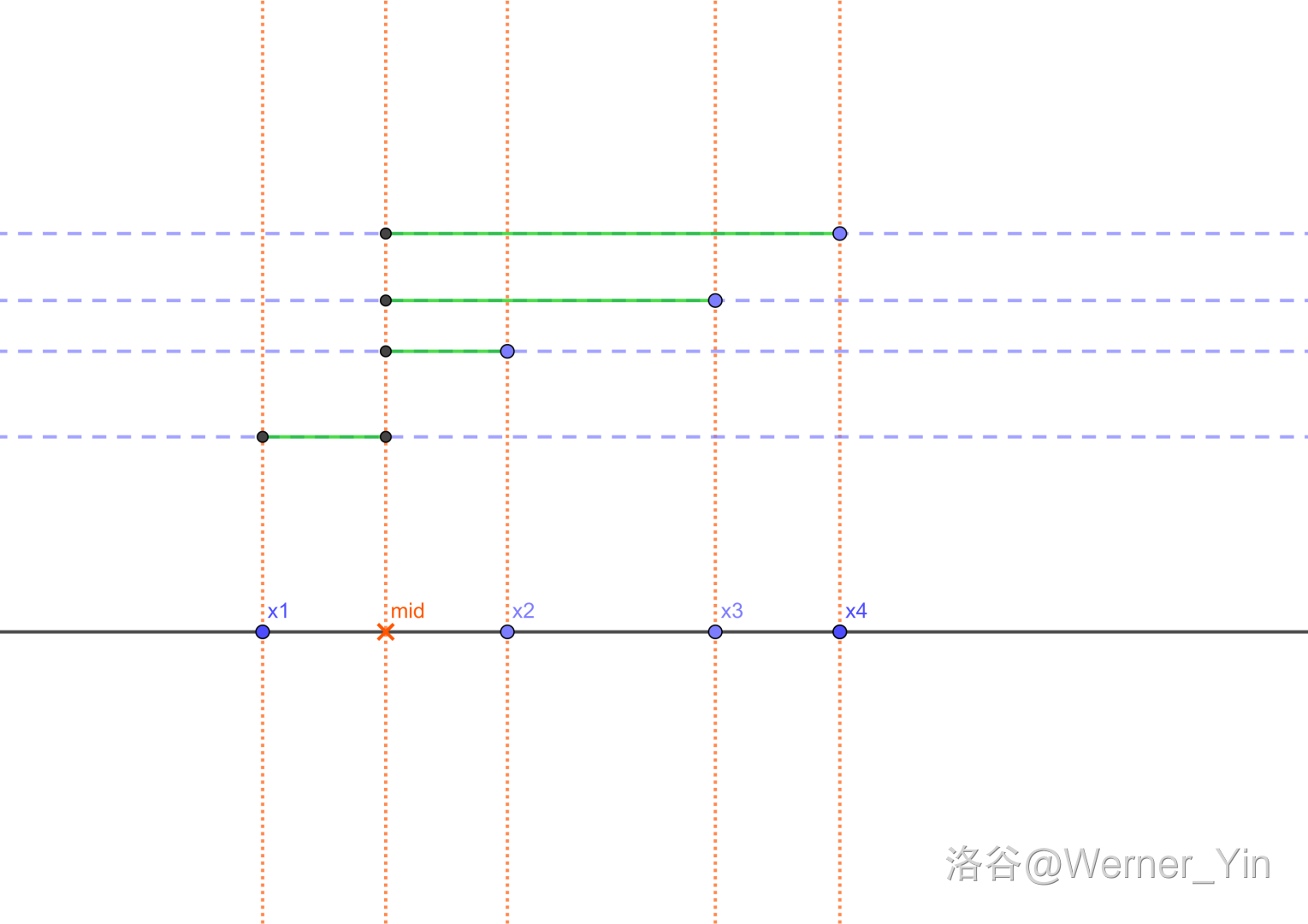
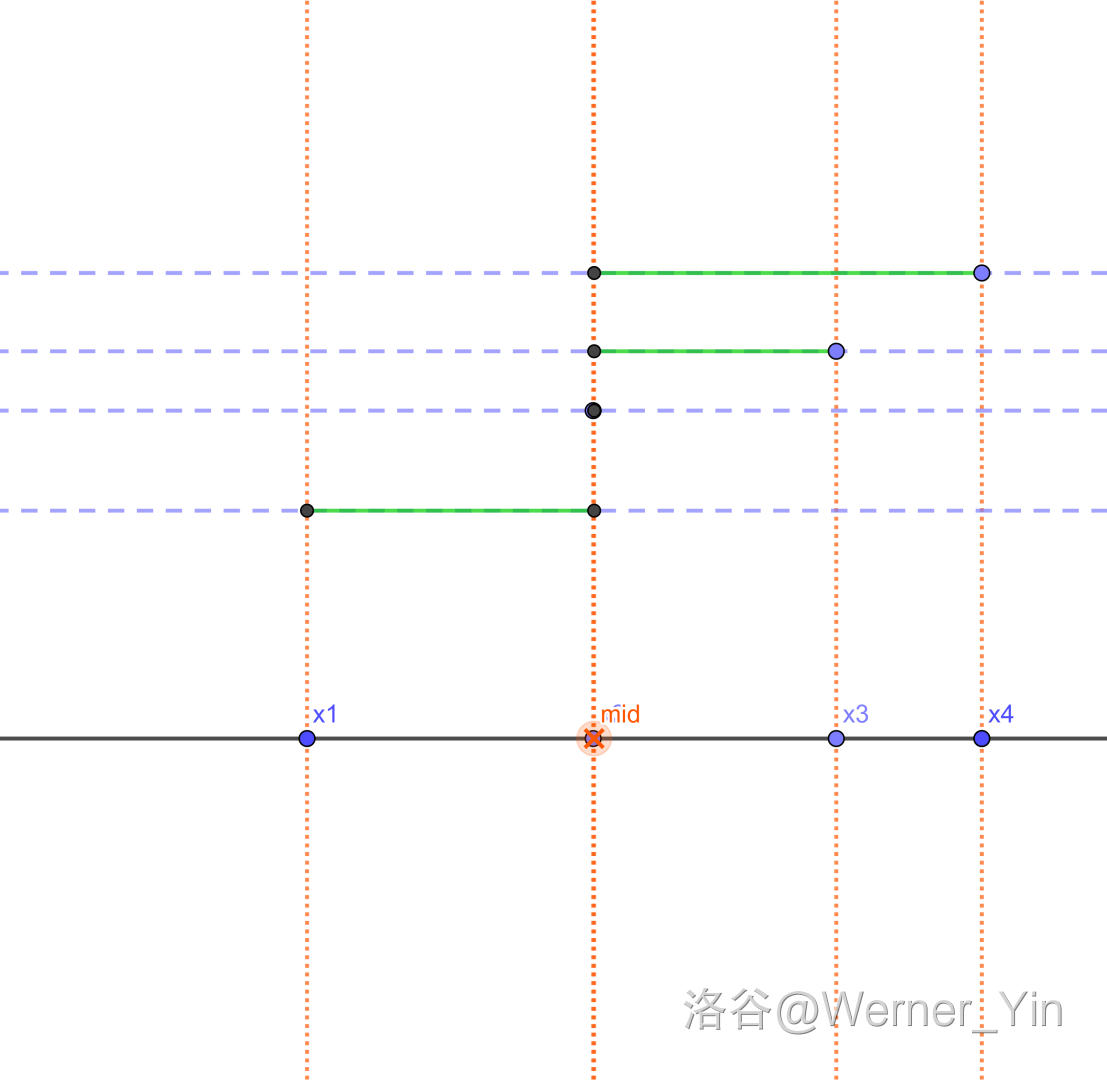
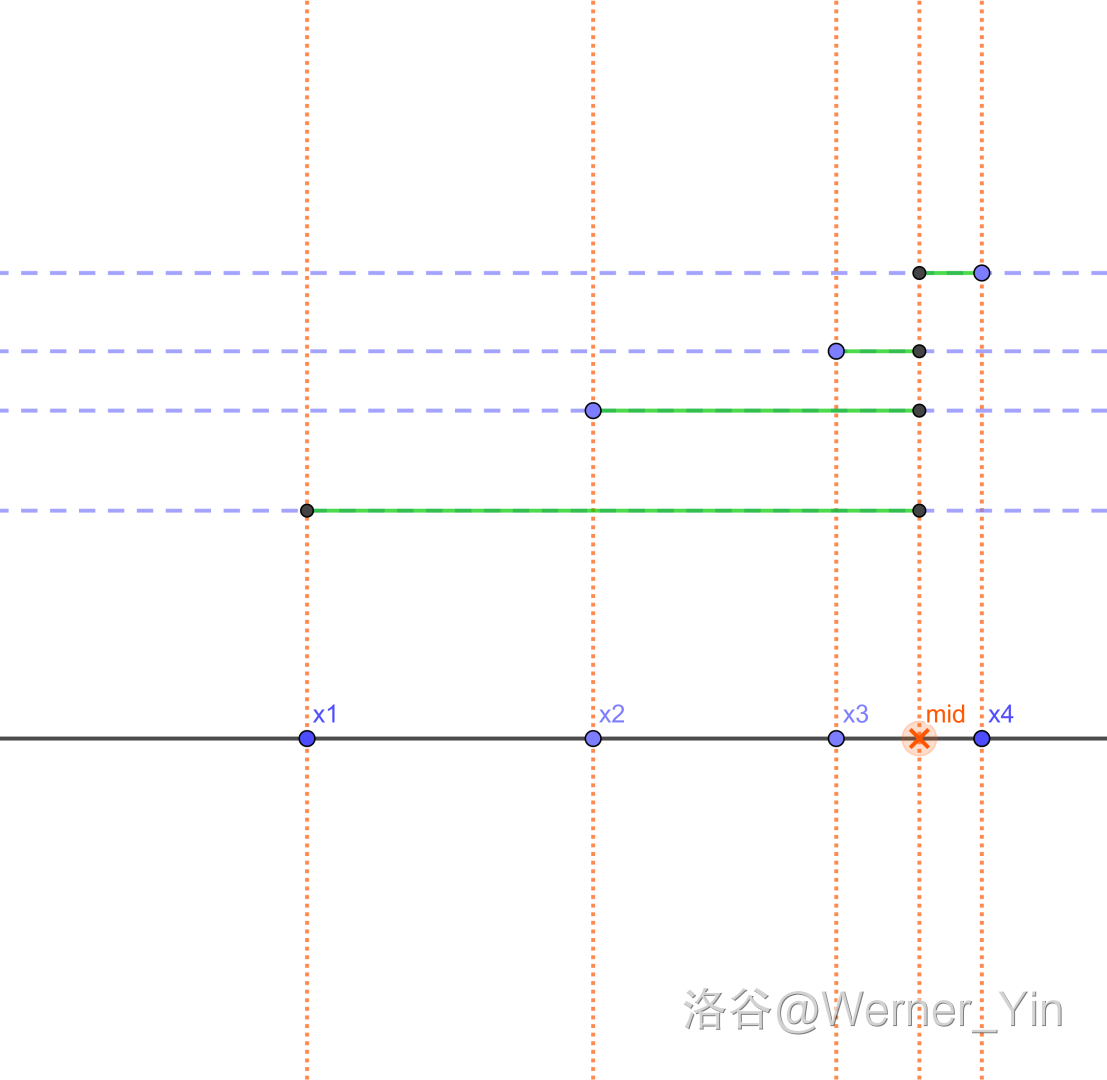
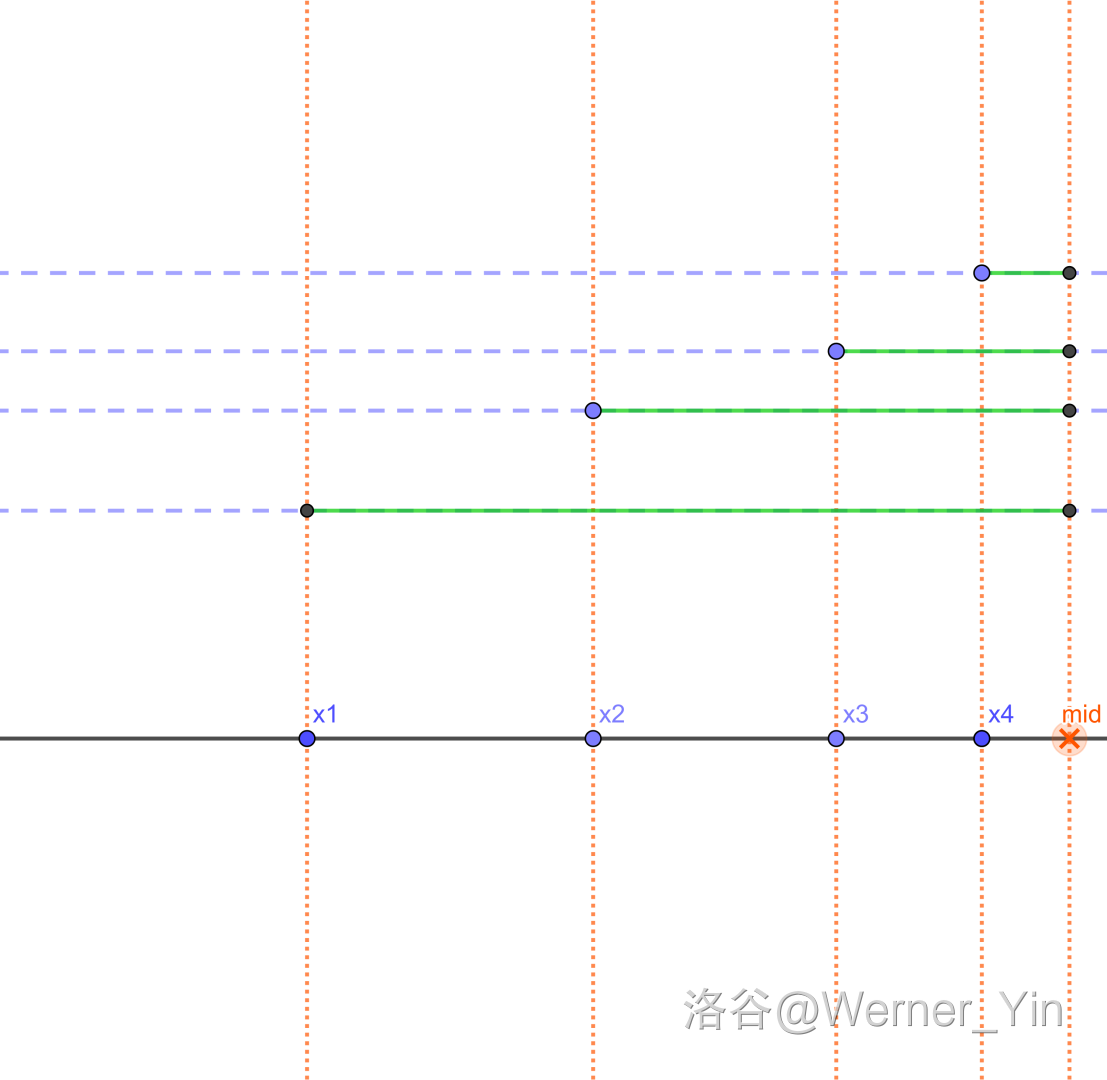
不管 (x_1,x_2,x_3,x_4) 的大小,我们都可以发现:
(x_2 <= mid <= x_3) 的情况最优。
因此,我们只要枚举 (mid = x_2) 或(mid = x_3) 就可以算答案了。
代码
#define re(x) read(x)
#define ll long long
using namespace std;
const int MAXN = 110;
const ll INF = 1e15;
int n,m,a[MAXN][MAXN];
int main (){
int T; re(T);
while(T--){
re(n);re(m);
for(int i = 1;i <= n;i++)
for(int j = 1;j <= m;j++)
re(a[i][j]);
ll ans = 0;
for(int i = 1;i <= n/2;i++){
for(int j = 1;j <= m/2;j++){ //每一行正中间的一个数无需考虑
ll tt = INF,sum;
sum = a[i][j];
tt = min(tt,abs(a[i][j]-sum) + abs(a[n-i+1][j]-sum)+abs(a[i][m-j+1]-sum) + abs(a[n-i+1][m-j+1]-sum));
sum = a[n-i+1][j];
tt = min(tt,abs(a[i][j]-sum) + abs(a[n-i+1][j]-sum)+abs(a[i][m-j+1]-sum) + abs(a[n-i+1][m-j+1]-sum));
sum = a[i][m-j+1];
tt = min(tt,abs(a[i][j]-sum) + abs(a[n-i+1][j]-sum)+abs(a[i][m-j+1]-sum) + abs(a[n-i+1][m-j+1]-sum));
sum = a[n-i+1][m-j+1];
tt = min(tt,abs(a[i][j]-sum) + abs(a[n-i+1][j]-sum)+abs(a[i][m-j+1]-sum) + abs(a[n-i+1][m-j+1]-sum));
ans += tt;
//注意,当时我写的时候没有排序,而是每个数进行枚举,因为数据量很小,所以可以过
}
if(m&1) ans += abs(a[i][m/2+1]-a[n-i+1][m/2+1]);
//如果有居中的行,只要满足这一行为回文的.
}
if(n&1){
for(int i = 1;i <= m/2;i++){
ans += abs(a[n/2+1][i] - a[n/2+1][m-i+1]);
}
}
write(ans);
}
return 0;
}