高度平衡树（AVL）

高度平衡树，又称 平衡二叉树。由Adelse-Velskil和Landis在1962年提出的高度平衡的二叉树，简称AVL树。

AVL结点

因为树的旋转，结点的高度可改变，需要重新定义结点的高等属性。

/// <summary>
/// AVL结点
/// </summary>
public class AVLNode<T> : BTNode<T> where T : IComparable<T>
{
    /// <summary>
    /// 当前结点的高度
    /// </summary>
    public new int Height { get; set; }
    /// <summary>
    /// 当前父结点
    /// </summary>
    public new AVLNode<T> Parent
    {
        get { return (AVLNode<T>)base.Parent; }
        set { base.Parent = value; }
    }
    /// <summary>
    /// 左子结点
    /// </summary>
    public new AVLNode<T> LeftChild
    {
        get { return (AVLNode<T>)base.LeftChild; }
        set { base.LeftChild = value; }
    }
    /// <summary>
    /// 右子结点
    /// </summary>
    public new AVLNode<T> RightChild
    {
        get { return (AVLNode<T>)base.RightChild; }
        set { base.RightChild = value; }
    }

    public AVLNode() : base() { }
    public AVLNode(T value) : base(value) { }

    public AVLNode(T value, int height, AVLNode<T> parent, AVLNode<T> left, AVLNode<T> right) : base(value, parent, left, right)
    {
        Height = height;
    }
}

实现

public class AVLTree<T> : BinarySearchTree<T> where T : IComparable<T>
{
    /// <summary>
    /// 返回根结点
    /// </summary>
    public new AVLNode<T> Root
    {
        get { return (AVLNode<T>)base.Root; }
        internal set { base.Root = value; }
    }

    public AVLTree() : base() { }

    /// <summary>
    /// 在树中插入元素
    /// </summary>
    /// <param name="item">插入项</param>
    public override void Insert(T item)
    {
        var node = new AVLNode<T>() { Data = item };
        if (InsertNode(node))
        {
            RebalanceTreeAt(node);
        }
        else
        {
            throw new InvalidOperationException("树不允许插入重复元素" + item.ToString());
        }
    }

    /// <summary>
    /// 从树中删除元素
    /// </summary>
    public override void Remove(T item)
    {
        if (IsEmpty)
        {
            throw new Exception("树是空的");
        }
        var node = FindNode(Root, item);
        if (Remove(node))
        {
            RebalanceTreeAt((AVLNode<T>)node);
        }
        else
        {
            throw new Exception("找不到元素项" + item.ToString());
        }
    }
    // TODO
}

在插入结点的过程中，会破坏AVL树的特性，旋转原则如下：

左-左型：做右旋；

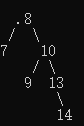
右-右型：做左旋转；

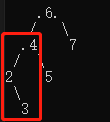
左-右型：先做左旋，后做右旋；

右-左型：先做右旋，再做左旋；

其他具体实现，同学们可根据AVL的特点，自行补充完善。

应用

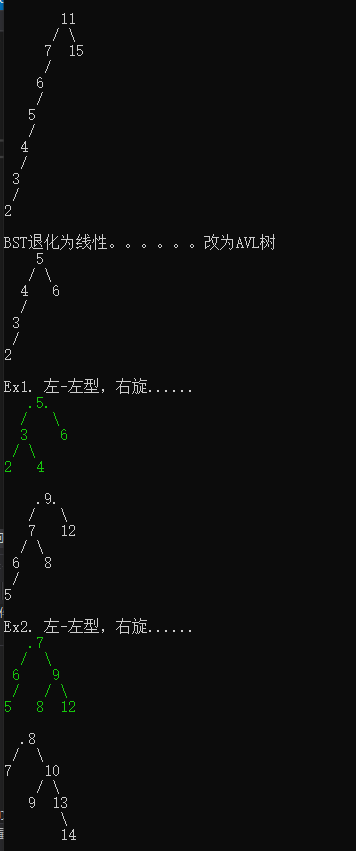
public void Test()
{
    var bst = new BinarySearchTree<int>();
    int[] values = new int[] { 11, 7, 15, 6, 5, 4, 3, 2 };
    bst.Insert(values);

    WsCommFunc.ConsoleWriteLine(bst.ToString(TraversalMode.LevelOrder));
    Console.WriteLine(TreeDrawer.DrawTree(bst));
    Console.WriteLine("BST退化为线性。。。。。。改为AVL树");


    var avl = new AVLTree<int>();
    values = new int[] { 5, 4, 6, 3, 2 };
    bst.Clear();
    bst.Insert(values);
    Console.WriteLine(TreeDrawer.DrawTree(bst));
    Console.WriteLine("Ex1. 左-左型，右旋......");
    avl.Clear();
    avl.Insert(values);
    WsCommFunc.ConsoleWriteLine(TreeDrawer.DrawTree(avl));

    values = new int[] { 9, 7, 12, 6, 8, 5 };
    bst.Clear();
    bst.Insert(values);
    Console.WriteLine(TreeDrawer.DrawTree(bst));
    Console.WriteLine("Ex2. 左-左型，右旋......");
    avl.Clear();
    avl.Insert(values);
    WsCommFunc.ConsoleWriteLine(TreeDrawer.DrawTree(avl));


    values = new int[] { 8, 7, 10, 9, 13, 14};
    bst.Clear();
    bst.Insert(values);
    Console.WriteLine(TreeDrawer.DrawTree(bst));
    Console.WriteLine("Ex3. 右-右型，左旋......");
    avl.Clear();
    avl.Insert(values);
    WsCommFunc.ConsoleWriteLine(TreeDrawer.DrawTree(avl));


    values = new int[] { 8, 7 };
    avl.Clear();
    avl.Insert(values);
    Console.WriteLine("Ex4. 原始树");
    Console.WriteLine(TreeDrawer.DrawTree(avl));
    Console.WriteLine("插入 6, 右旋");
    avl.Insert(6);
    Console.WriteLine(TreeDrawer.DrawTree(avl));
    Console.WriteLine("插入 9");
    avl.Insert(9);
    Console.WriteLine(TreeDrawer.DrawTree(avl));
    Console.WriteLine("插入 10, 左旋");
    avl.Insert(10);
    Console.WriteLine(TreeDrawer.DrawTree(avl));
    Console.WriteLine("插入 11, 左旋");
    avl.Insert(11);
    Console.WriteLine(TreeDrawer.DrawTree(avl));
    Console.WriteLine("插入 12, 左旋");
    avl.Insert(12);
    Console.WriteLine(TreeDrawer.DrawTree(avl));
    Console.WriteLine("插入 15");
    avl.Insert(15);
    Console.WriteLine(TreeDrawer.DrawTree(avl));
    Console.WriteLine("插入 14，先右旋，再左旋");
    avl.Insert(14);
    Console.WriteLine(TreeDrawer.DrawTree(avl));
    Console.WriteLine("删除最大值 15");
    avl.RemoveMax();    //avl.Remove(15);
    Console.WriteLine(TreeDrawer.DrawTree(avl));
    Console.WriteLine("插入 13，先左旋，再右旋");
    avl.Insert(13);
    Console.WriteLine(TreeDrawer.DrawTree(avl));

}