八大排序算法之七-归并排序

归并类的排序算法

归并：将两个或两个以上的有序表组合成一个新的有序表。

内部排序中，通常采用的是 2-路归并排序。即：将两个位置相邻的记录有序子序列归并为一个记录有序的序列。归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

图解如下

看成是 n 个有序的子序列（长度为 1），然后两两归并。

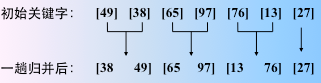
得到 n/2 个长度为2 或 1 的有序子序列。继续亮亮归并

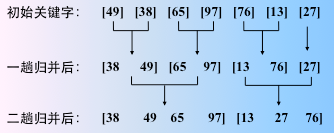
最后一趟

代码如下：

#include<iostream>
#include <cstdlib>
using namespace std;
////二路一次归并过程的算法
void Merge(int a[],int low,int mid,int high)
{
     //mid+1为第2有序区第1个元素，mid为第1有序区的最后1个元素
     //i 指向第 1 有序区的第 1 个元素
    int i=low;
    int j=mid+1;
    int *temp=new int[high-low+1];
    //内存分配失败
    if(!temp)
    {
        cout<<"数组分配失败";
        exit(0);
    }
    int k=0;
    //顺序选取两个有序区的较小元素，存储到t数组中，因为是递增排序
    while(i<=mid&&j<=high)
    {
        if(a[i]<=a[j])
            temp[k++]=a[i++];
        else
        {
            temp[k++]=a[j++];
        }
    }
    //比完之后，假如第1个有序区仍有剩余，则直接全部复制到 temp 数组
    while(i<=mid)
    {
        temp[k++]=a[i++];
    }
    //比完之后，假如第2个有序区还有剩余，则直接全部复制到 temp 数组
    while(j<=high)
    {
        temp[k++]=a[j++];
    }
     //将排好序的序列，重存回到 a 中 low 到 high 区间
    for(i=low,k=0;i<=high;i++,k++)
    {
        a[i]=temp[k];
    }
    delete[]temp;
}
void mergeSort(int a[],int low,int high)
{
    //二路归并排序，分为二路
    int mid=(low+high)/2;
    if(low<high)
    {
        ////递归过程，二路归并排序递归过程
        mergeSort(a,low,mid);
        mergeSort(a,mid+1,high);
        //归并
        Merge(a,low,mid,high);
    }
}
int main()
{
    int source[]={49,38,65,97,76,13,27};
    mergeSort(source,0,6);
    for(int i=0;i<7;i++)
    {
        cout<<source[i]<<" ";
    }
    return 0;
}