斐波那契数列问题是算法学习者必定接触到的问题。作为经典问题,首次接触时通常是作为递归算法的案例教程。
然而递归解决斐波那契。其效率低的令人发指,有人算出其时间复杂度为O(2^n)。指数级时间复杂度。
假设面试的时候面试官问你斐波那契的求解方法,你来一个递归求解,基本上能够说,你已经game over了。
那么有没有更高效的算法呢。本文将一一介绍。
以下是斐波那契的4种解法:
1.递归 时间复杂度O(2^n)
int f(int n){
if(n == 1 || n == 2){
return 1;
}
return f(n-1) + f(n-2);
}2.循环 时间复杂度O(n)
public int f(int n) {
// write code here
int f0 = 1;
int f1 = 1;
int f2 = 0;
for(int i = 2; i < n; i++){
f2 = f0 + f1;
f0 = f1;
f1 = f2;
}
return f2;
}
斐波那契的递推公式能够表示成例如以下矩阵形式。所以其
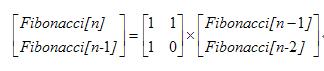
所以依据矩阵的分治算法。能够在O(logn)时间内算出结果。
笔试问题:
对于斐波拉契经典问题。我们都很熟悉。通过递推公式F(n) = F(n - 1) + F(n - 2),我们能够在线性时间内求出第n项F(n),如今考虑斐波拉契的加强版,我们要求的项数n的范围为int范围内的非负整数,请设计一个高效算法,计算第n项F(n)。
第一个斐波拉契数为F(0) = 1。
给定一个非负整数,请返回斐波拉契数列的第n项,为了防止溢出,请将结果Mod 1000000007。
long[][] f = new long[][]{{0,1},{1,1}};
public int getNthNumber1(int n) {
if(n == 0)
return 1;
if(n == 1)
return 1;
f = pow(n,f);
return (int) f[1][1];
}
private long[][] pow(int n,long[][] f){
if(n == 1)
return f;
if(n == 2){
return fun(f,f);
}
if( n % 2 == 0){//偶数
f = pow(n/2,f);
return fun(f, f);
}else{
return fun(pow(n/2,f),pow(n/2 + 1,f));
}
}
private long[][] fun(long[][] f,long[][] m){
long[][] temp = new long[2][2];
temp[0][0] = (f[0][0]*m[0][0] + f[0][1]*m[1][0])%1000000007;
temp[0][1] = (f[0][0]*m[0][1] + f[0][1]*m[1][1])%1000000007;
temp[1][0] = (f[1][0]*m[0][0] + f[1][1]*m[1][0])%1000000007;
temp[1][1] = (f[1][0]*m[0][1] + f[1][1]*m[1][1])%1000000007;
return temp;
}
4.公式求解 时间复杂度O(1)
对,你没看错。斐波那契数列是有求解公式的。其通项公式例如以下:

所以,不论什么斐波那契数都能够在O(1)时间内计算出来,可是有一点,由于牵涉到无理数。所以无法保证精度。
详细代码略。
综上,眼下代码效率最高也最准确的,是第3种矩阵求解方法,笔试面试时务必掌握。
【完】