首先将原图中的连通分量缩点,一定可以将原图缩成一棵树的形式,然后统计这棵树的叶子节点个数,答案就是(leaf+1)/2。这里不再证明,可以画个图看一下。
(简单说明一下,首先把两个最近公共祖先最远的两个叶节点之间连接一条边,这样可以把这两个点到祖先的路径上所有点收缩到一起,因为一个形成的环一定是双连通的。然后再找两个最近公共祖先最远的两个叶节点,这样一对一对找完,恰好是(leaf+1)/2次,把所有点收缩到了一起。 --Byvoid)
怎么统计呢?用并查集缩点,可以知道,缩点后留下的边全部是原图的桥,这是我们可以用Tarjan求出原图的所有桥,然后枚举每条桥,桥两端的点度数分别+1,就可以求出每个点(缩点后的点)的度数了,找出度数为1的即为叶子节点。
怎么用Tarjan求桥呢?根据Tarjan算法性质可知,若low[v]>dfn[u],则边(u,v)为桥(v被封死在子树内)
如图,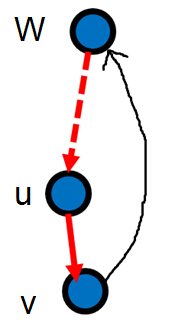 若low[v]>dfn[u],则v被封死在u的子树内,删除点u,或者删除边(u,v),都将使v与u的祖先w不连通。
若low[v]>dfn[u],则v被封死在u的子树内,删除点u,或者删除边(u,v),都将使v与u的祖先w不连通。
关于Tarjan求桥可见:http://hi.baidu.com/lydrainbowcat/item/f8a5ac223e092b52c28d591c
代码:

#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <algorithm> #include <string> #include <vector> #include <map> #include <set> #include <time.h> #include <queue> #include <cctype> #include <utility> #include <numeric> #include <cstdlib> #include <functional> #include <iomanip> #include <sstream> #define Mod 1000000007 #define SMod 10007 #define INT 2147483647 #define pi acos(-1.0) #define eps 1e-4 #define lll __int64 #define ll long long using namespace std; #define N 10007 vector<int> G[N]; struct Bridge { int u,v; }bg[2*N]; int vis[N],low[N],dfn[N],Time; int fa[N],deg[N]; int n,m,cnt; int findset(int x) { if(x != fa[x]) fa[x] = findset(fa[x]); return fa[x]; } void Tarjan(int u,int father) { low[u] = dfn[u] = ++Time; vis[u] = 1; for(int i=0;i<G[u].size();i++) { int v = G[u][i]; if(v == father) continue; if(!vis[v]) { Tarjan(v,u); low[u] = min(low[u],low[v]); if(low[v] > dfn[u]) //u->v为桥 bg[cnt].u = u,bg[cnt++].v = v; else //否则,u,v同属一个连通分量,合并 { int fx = findset(u); int fy = findset(v); if(fx != fy) fa[fx] = fy; } } else low[u] = min(low[u],dfn[v]); } } int main() { int i,j,u,v; while(scanf("%d%d",&n,&m)!=EOF) { for(i=0;i<=n;i++) G[i].clear(); cnt = Time = 0; for(i=0;i<m;i++) { scanf("%d%d",&u,&v); G[u].push_back(v); G[v].push_back(u); } for(i=1;i<=n;i++) fa[i] = i; memset(dfn,0,sizeof(dfn)); memset(low,0,sizeof(low)); memset(vis,0,sizeof(vis)); Tarjan(1,-1); //统计桥端度数 memset(deg,0,sizeof(deg)); for(i=0;i<cnt;i++) { int fx = findset(bg[i].u); //fx,fy为缩点后的代表点 int fy = findset(bg[i].v); deg[fx]++; deg[fy]++; } int leaf = 0; for(i=1;i<=n;i++) if(deg[i] == 1) leaf++; printf("%d ",(leaf+1)/2); } return 0; }
