DS博客作业2--线性表

0.PTA得分截图

1.本周学习总结

1.1 总结线性表内容

• 顺序表

1.顺序表结构体定义

#define MaxSize 50        //设置线性表最大长度，方便修改
typedef int ElemType;            //为int类型取别名ElemType
typedef struct
{
    ElemType data[MaxSize];            //定义数组存放线性表元素
    int length;                    //记录线性表长度
}SqList，*List;            //定义顺序表类型

2.顺序表的建立

void CreatList(List &L,ElemType a[],int n)            //由传入的a中的n个元素来建立线性表
{
    int i=0；            
    int k=0;            //k表示L中元素个数，开始顺序表为空，所以K初始值为0

    L=new SqList;            //给顺序表分配空间

    while(i<n)                //利用while循环扫描数组a
    {
    L->data[k]=a[i];            //将数组a中的元素a[i]放入L中
    k++;                
    i++;
    }

    L->length=k;                   //记录顺序表长度为k
}

3.顺序表的元素插入(利用布尔类型来返回插入结果，返回True表示插入成功，返回False表示插入失败）

bool ListInsert(List &L,int i,ELemType e)
{
    int j;
    if(i<1||i>L->lengeh+1)            //若参数i小于1或者大于数组长度+1，则改参数错误，返回False
    {
        return False;
    }

    i--;                                //将插入位置的逻辑序号转换成为对应的物理序号

    for(j=L->length;j>i;j--)            //若该位置存在，则将该位置及其后的所有元素后移一位
    {
        L->data[j]=L->data[j-1];
    }

    L->data[i]=e;                        //将待插入元素e插入
    L->length++;                         //因为插入一个元素，所以顺序表元素多了一个，顺序表长度增1
    return True;                         //插入成功，返回True

4.顺序表元素的删除(利用布尔类型来返回删除结果）

bool ListDelete(List &L, int i, ElemType &e)
{
    int j;
    
    if(i<1||i>L->lengeh+1)            //若参数i小于1或者大于数组长度+1，则改参数错误，返回False
    {
        return False;
    }

    i--;

    e=L->data[i];            
    
    for(j=i;j<L->length;j++)        //利用循环覆盖第i个值
    {
        L->data[j]=L->data[j+1];
    }
    
    L->length--;            //因为成功删除第i个值，元素少了一个，顺序表长度减1
    return True;            //删除成功，返回True
}

• 链表

1.链表结构体定义

typedef int ElemType;
typedef struct LNode
{
    ElemType data;
    struct LNode *next;
}LinkNode,*LinkList;

2.头插法，尾插法建链表

 //头插法建链表
void CreateListF(LinkList& L, int n)           
{

	L =  new LNode;
	L->next = NULL;
        LinkList p;

	while (n--)
	{
		p =  new LNode;
		cin >> p->data;
		p->next = L->next;
		L->next = p;
	}
}

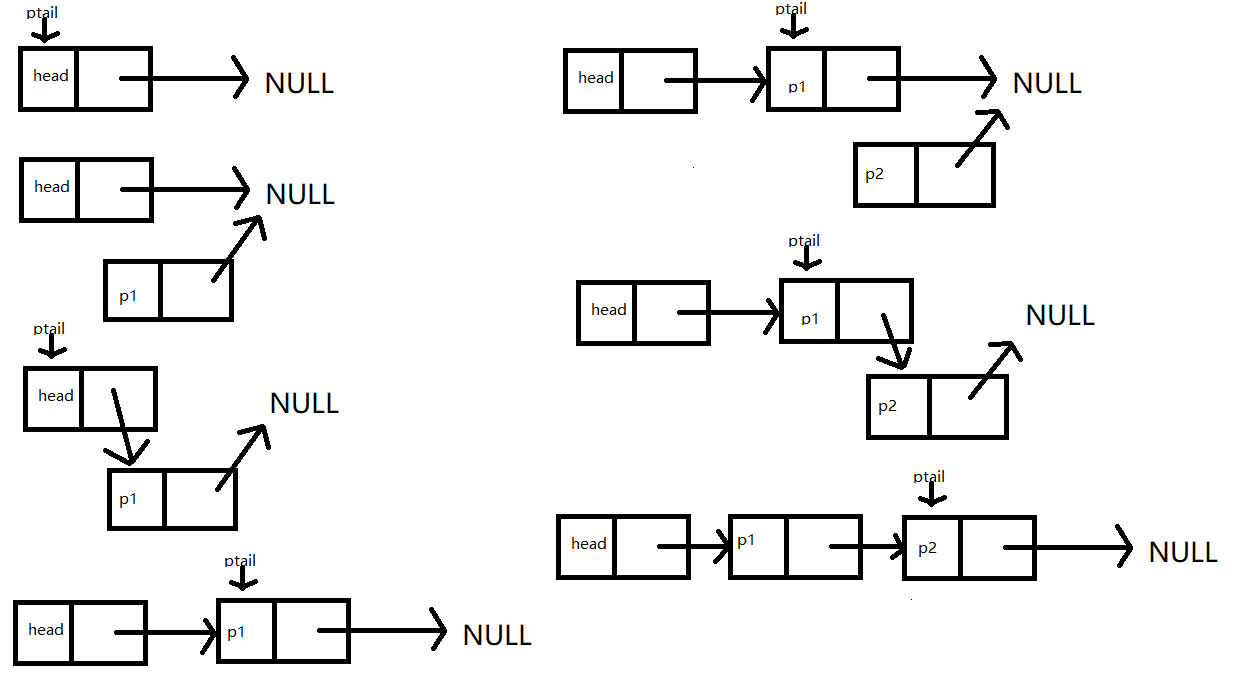
//尾插法建链表
void CreateListR(LinkList& L, int n)                
{
	L = new LNode;
	LinkList p;
	LinkList ptail = L;                
	ptail->next = NULL;
	while (n--)
	{
		p = new LNode;
		cin >> p->data;
		ptail->next = p;
		ptail = p;
	}
	ptail->next = NULL;
}

3.链表插入

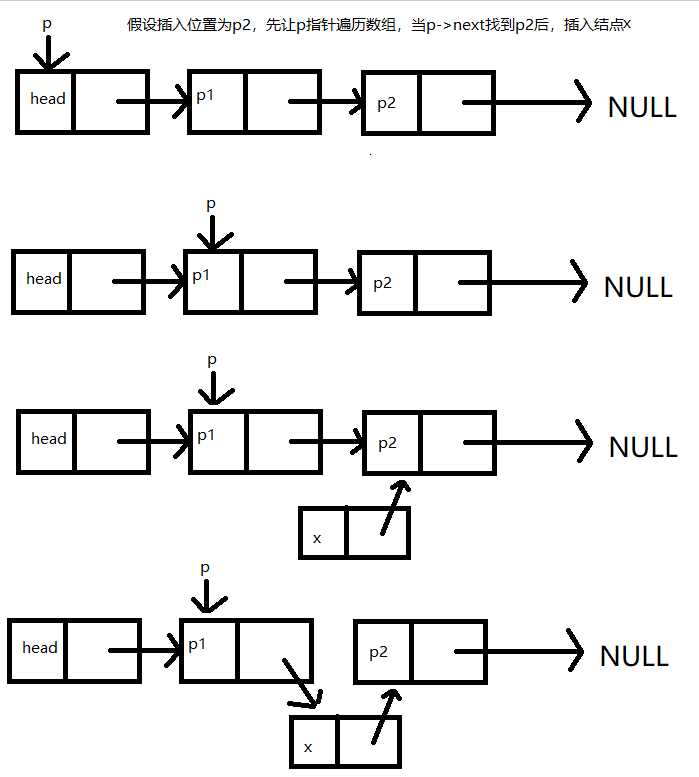
void ListInsert(Linklist& L, int i, ElemType e) 
{  
	LinkList p;
	p = L->next;
	j = 0;

	while (p && j < i - 1) 
	{
		p = p->next;
		j++;
	}

	if (!p || i <= 0) 
	{
		cout << "位置错误！" << endl;
	}
	else
	{
		s = new node();
		s->data = e;
		s->next = p->next;
		p->next = s;
	}
}

4.链表删除

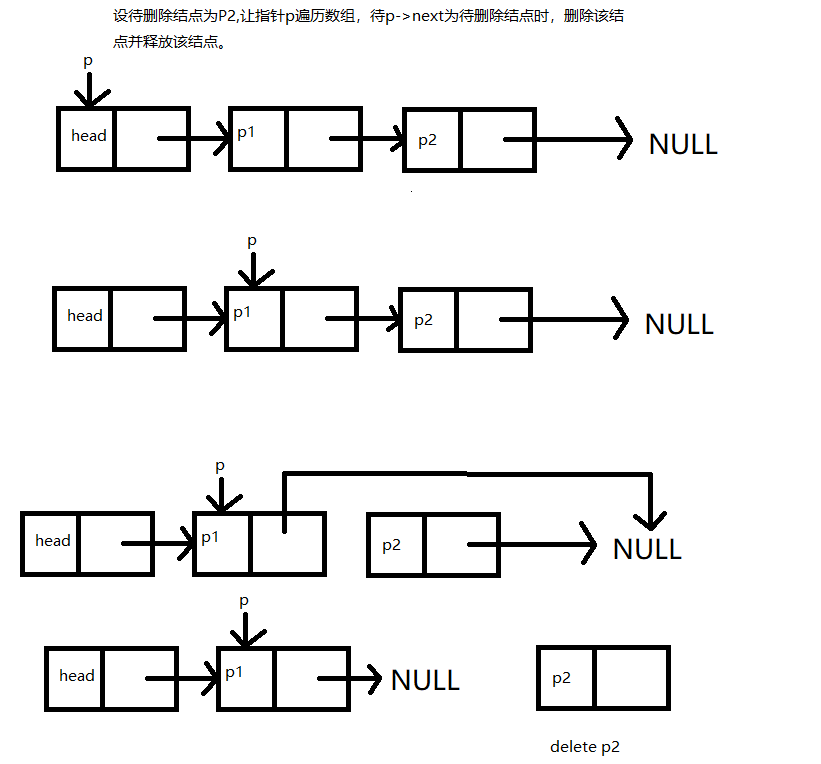
void ListDelete(Linklist& L, int i) 
{  
	LinkList p;
	p = L->next;
	j = 0;

	while (p->next && j < i - 1) 
	{
		p = p->next;
		j++;
	}

	if (!p || i <= 0) 
	{
		cout << "位置错误！" << endl;
	}
	else
	{
		s = new node();
		s = p->next;
		p->next = p->next->next;
		delete s;
	}
}

5.链表分割

void SplitList(LinkList& L, LinkList& L1, LinkList& L2)
{
	LinkList p;
	LinkList prev;
	LinkList ptail;
	L2 = new LNode;
	prev = L->next;
	L1 = L;
	L1->next = NULL;
	L2->next = NULL;
	
	ptail = L1;
	int i;

	for (i = 1; prev; i++, prev = prev->next)
	{
		p = new LNode;
		p->data = prev->data;
		p->next = NULL;

		if (i % 2 == 1)
		{
			ptail->next = p;
			ptail = p;
		}
		else
		{
			p->next = L2->next;
			L2->next = p;
		}

	}
}

• 有序表（有序单链表）

1.插入

void ListInsert(LinkList& L, ElemType e)
{
	LinkList x = L;                    
	LinkList p = new LNode;            //新开辟p一个节点存储传入的值e
	p->data = e;                       
	while (x->next && x->next->data < e)            //利用while循环来寻找插入位置
	{
		x = x->next;
	}
	p->next = x->next;                    //将存储e的新节点插入找到的位置中
	x->next = p;
}

2.删除

void ListDelete(LinkList& L, ElemType e)
{
	int flag = 1;                        //利用flag来判断成功删除传入数据e，给flag赋初值1
	LinkList x = new LNode;
	LinkList p = L;                

	x->next = NULL;

	if (p->next == NULL)
	{
		return;
	}
	while (p->next)                //利用while循环来寻找待删除元素，一旦找到该待删除元素，终止循环，并将flag的值变为e
	{
		if (p->next->data == e)
		{
			x = p->next;
			p->next = x->next;
			flag = 0;
                        delete x;                        //找到该元素之后链表中删除该元素，并释放该节点
			break;
		}
		p = p->next;
	}
	if (flag == 1)                            //若未找到该元素，则输出"找不到！"
	{
		cout << e << "找不到！" << endl;
	}
}

3.有序表合并

void MergeList(LinkList &L1,LinkList L2)
{
    LinkList p, head;
    head = L1;
    while (L2->next&&head->next)
    {
        if (head->next->data > L2->next->data)
        {
            p = new LNode;
            p->data = L2->next->data;
            p->next = head->next;
            head->next = p;
            L2 = L2->next;
        }
        else if(head->next->data == L2->next->data)
        {
            L2 = L2->next;
        }
        head = head->next;
    }
    if (head->next == NULL)
    {
        head->next = L2->next;
    }
}

• 双向链表操作

1.链表结构体定义

void CreateDListF(DLinkList& L, int n, DLinkList& Lr);	//头插法建立链表
void CreateDListR(DLinkList& L, int n, DLinkList& Lr);	//尾插法创建链表
void DispDListF(DLinkList L);		//正向输出链表
void DispDListR(DLinkList L, DLinkList Lr);		//反向输出链表
void InsertDList(DLinkList& L, int i, ElemType e)；        //数据插入
void DestroyDList(DLinkList& L);		//销毁链表

int main()            
{
	DLinkList L;
	DLinkList Lr;		//存储链表尾结点，方便反向对链表进行操作
	int n;
	cin >> n;
	CreateDList(L, n, Lr);
	DispDListF(L);
	DispDListR(L, Lr);
	DestroyList(L);
	return 0;
}

1.双向链表的结构体定义

typedef int ElemType;
typedef struct node
{
	ElemType data;
	struct node* pre;        //指向前一节点的指针
	struct node* next;       //指向后一节点的指针
}DLNode, *DLinkList;

2.双向链表建立

//尾插法
void CreateDListR(DLinkList& L, int n, DLinkList& Lr)
{
	L = new DLNode;
	L->next = NULL;
	L->pre = NULL;
	DLinkList p, ptail;
	ptail = L;
	while (n--)
	{
		p = new DLNode;
		cin >> p->data;
		p->next = ptail->next;
		ptail->next = p;
		p->pre = ptail;
		ptail = p;
	}
	Lr = ptail;
}

//头插法
void CreateDListF(DLinkList& L, int n, DLinkList& Lr)
{
	int flag = 1;
	L = new DLNode;
	DLinkList p;
	L->next = NULL;
	L->pre = NULL;
	while (n--)
	{
		p = new DLNode;
		cin >> p->data;
		p->next = L->next;
		if (L->next != NULL)
		{
			L->next->pre = p;
		}
		if (flag == 1)
		{
			Lr = p;
			flag = 0;
		}
		L->next = p;
		p->pre = L;
	}
}

3.链表输出

//正向输出链表
void DispDListF(DLinkList L)
{
	DLinkList p;
	p = L->next;
	if (p != NULL)
	{
		while (p->next)
		{
			cout << p->data << " ";
			p = p->next;
		}
		cout << p->data << endl;
	}
	else
	{
		cout << "空链表！" << endl;
	}
}

//反向输出链表
//利用主函数中存储的尾结点位置，直接反向输出链表
void DispDListR(DLinkList L, DLinkList Lr)
{
	DLinkList p;
	p = Lr;
	while (p->pre->pre)
	{
		cout << p->data << " ";
		p = p->pre;
	}
	cout << p->data << endl;
}

4.双向链表的数据插入

void InsertDList(DLinkList& L, int i, ElemType e)
{
	int j = 0;
	DLinkList p, s;
	p = L;
	if (i <= 0)
	{
		cout << "位置无效！" << endl;
		return;
	}

	while (p && j < i - 1)
	{
		j++;
		p = p->next;
	}

	if (p == NULL)
	{
		cout << "位置无效！" << endl;
		return;
	}
	else
	{
		s = new DLNode;
		s->data = e;
		s->next = p->next;
		if (p->next != NULL)
		{
			p->next->pre = s;
		}
		s->pre = p;
		p->next = s;
	}

}

结构特点：有两个指针，一个指向后继节点，一个指向前驱结点。相较于单链表，双向链表对某结点的前后结点的访问更加方便。

• 单循环链表

1.结构体定义

typedef int ElemType;
typedef struct node
{
	ELemType data;
	struct node* next;
}CLNode, *CLLinkList;

2.单循环链表的建立

void CreateListR(CLLinkList& L, int n)                
{
	L = new LNode;
	LinkList p;
	LinkList ptail = L;                
	ptail->next = NULL;
	while (n--)
	{
		p = new LNode;
		cin >> p->data;
		ptail->next = p;
		ptail = p;
	}
	ptail->next = L;
}

结构特点：链表呈环状，可以从链表的任意位置对整个链表进行遍历

1.2 学习体会

使用链表存储数据较为简便，方便对存储数据进行插入、删除等改动。
在学习过程中，主要遇到的问题有两点：
1.开始的时候对链表的操作不熟练，导致循环时判断条件的使用错误，导致循环结束的位置不正确。
2.在使用循环的时候因为没有转换思维，喜欢使用两层循环，导致提交时产生运行超时的问题。

2.PTA实验作业

2.1 有序链表合并

• 2.1.1 代码截图
  
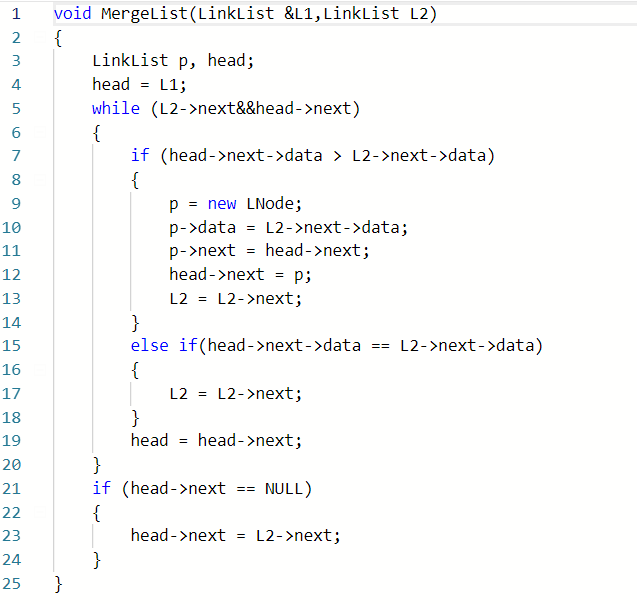
• 2.1.2 本题PTA提交列表说明
  
  Q1:第一次在合并链表的时候，遇到相同元素我并未删除，而是将两个元素一起放入链表。
  A1:发现这个问题之后，在两个数据相同是，我删除了第二个表的数据，将第一个表的数据放入新合并的表中

2.2 有序链表合并

• 2.1.1 代码截图
  
• 2.1.2 本题PTA提交列表说明
  
  Q1:第一次因为分割时操作不当导致原有链断裂，导致代码运行出错
  A1:新开辟结点存储数据，加入第二条链，是原有链不断裂
  Q2:未注意题中的要求第二条链为倒序
  A2:对第二条链使用头插法

2.2 有序链表合并

• 2.1.1 代码截图
  
  
  

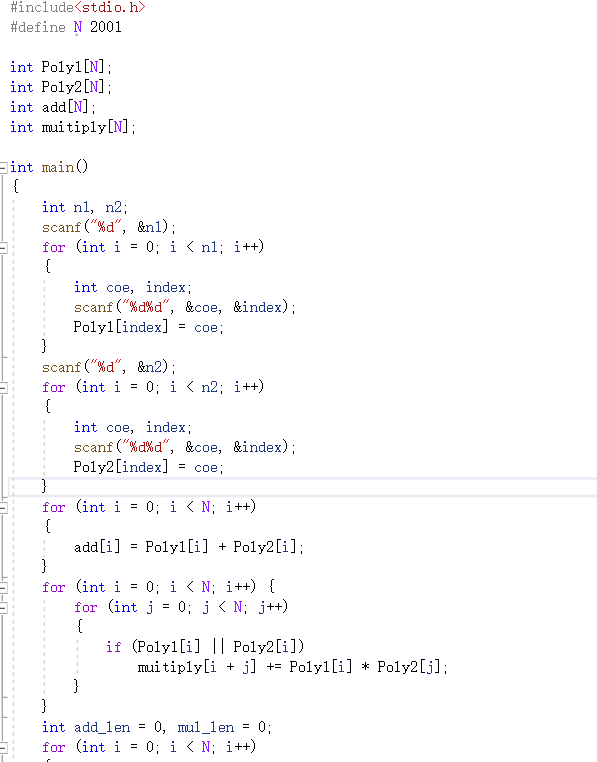
• 2.1.2 本题PTA提交列表说明
  
  Q1:第一次使用链表存储，由于对链表操作的不熟悉，导致存储时代码出问题，无法编译
  A1:后使用数组存储，内容存储系数，下表为指数

3.阅读代码

3.1 题目及解题代码

题目：[LeetCode] Palindrome Linked List 回文链表

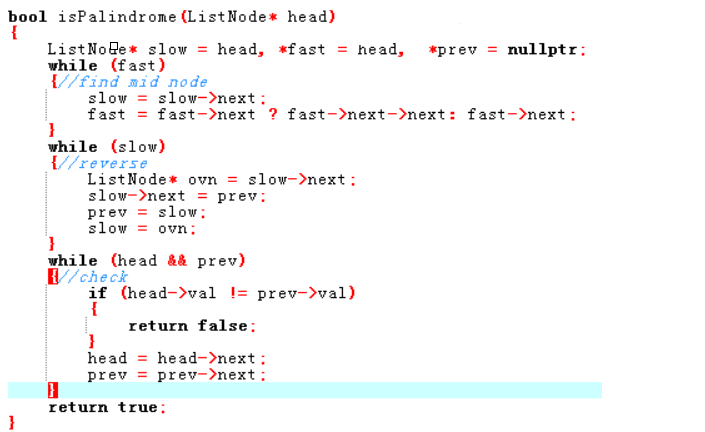
3.1.2 该题的伪代码

• 快慢指针找中点的原理：fast和slow两个指针，每次快指针走两步，慢指针走一步，等快指针走完时，慢指针的位置就是中点
• 首先，find mid node 使用快慢指针找到链表中点。 然后，reverse 逆序后半部分，使用头插法，将后半部分的数据进行倒置。 最后，check，head和pre两个指针同时进行遍历比较是否相同。如果相同返回true，有不同返回false
  

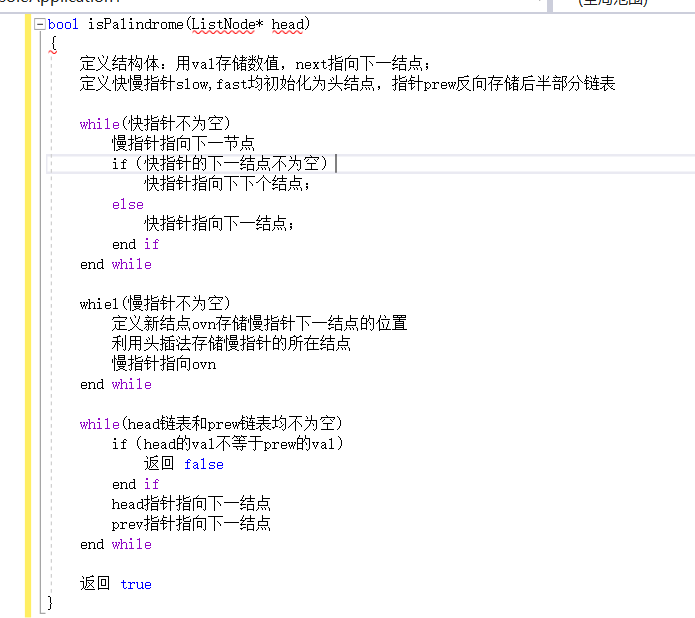
代码只遍历了一次数组，时间复杂度为O(n)
没有使用任何临时存储结构，空间复杂度为O(1)

3.1.3 运行结果

3.1.4分析该题目解题优势及难点

本题使用快慢指针来判断中点位置，并且在中点处将后续链表倒置，来判断前后是否一致，较为简便。
难点在于判断中点位置,及将链表倒置

3.1 题目及解题代码

链表的中间结点
输入：[1,2,3,4,5]
输出：此列表中的结点 3 (序列化形式：[3,4,5])
返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。
注意，我们返回了一个 ListNode 类型的对象 ans，这样：
ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL

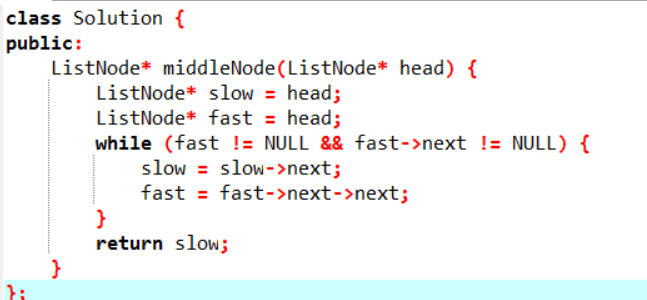
3.1.1 该题的设计思路

当用慢指针 slow 遍历列表时，让另一个指针 fast 的速度是它的两倍。当 fast 到达列表的末尾时，slow 必然位于中间。
由于本题未使用临时存储空间，空间复杂度为O(1)
本题只遍历一次链表，时间复杂度为O(n)

3.1.2 该题的伪代码

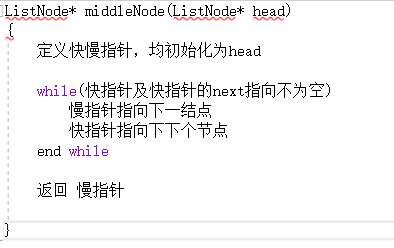
3.1.3 运行结果

3.1.4分析该题目解题优势及难点

可以使用快慢指针，方便解题
难点在于利用快慢指针寻找中间结点，并且在中间结点有两个时，我提交时发现需要输出第二个结点