引入
RMQ问题:
给定一个长度为(n)的序列(A_{1 - n}),有(q)次询问,每次询问给出(x,y),回答(A_{x-y})中的最大值(也可以是最小值,此处以最大值为例)
通常(n,q leq 100000)。
利用倍增解决这类问题的算法叫做ST表。
ST表
对于序列(A_{1-n}),我们构造一个二维数组(st[1-n] [0-log_2 n]),(st[i] [j])表示从(i)这个位置开始,往后(2^j)个位置中的最大值(包括(i))。
利用倍增思想构造:
初始化:(st[i] [0] = a_i)。
除此之外,对于任何一个(st[i] [j])所表示的区间,我们从中间划分成两段,起点分别为(i)和(i + 2^j)。根据倍增:
$st[i] [j] = max{(st[i][j - 1], st[i + (1 << j - 1)][j - 1])} $.
先从(1-log_2 n)枚举(j),在顺序枚举(i),构造即可。
构造时间复杂度:(O(nlog n)).
查询区间最大(最小)值
对于每一次给出的(x,y),其长度为(len),先找出小于等于(len)的最大的(2)的整数次幂,例如为(2^k)
那么可以用前(2^k)与后(2^k)两段来完全覆盖该([x-y])区间,所以:
(ans = max{(st[x][k], st[y - (1 << k) + 1][k])}).
其中(k) 在代码中可写为:(k = (int)(log(y - x + 1) / log(2))).
查询时间复杂度:(O(1)).
可谓是很优秀了。
用ST表解决LCA问题
欧拉序: 对于一棵树,我们在遍历整棵树时,将我们经过的节点编号依次记录下来,所得到的序列叫做树的欧拉序。
例如:
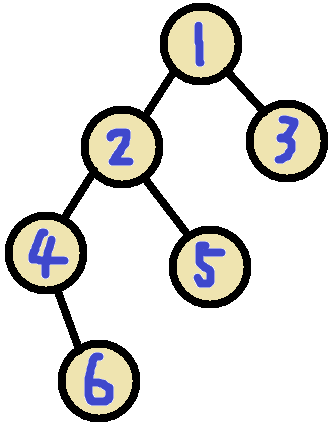
该树的欧拉序:(1-2-4-6-4-2-5-2-1-3-1)
易证欧拉序的长度为(2n-1)
我们用(c)数组记录欧拉序,令(s_i)表示(i)在(c)中出现的位置,如:
上图中的(s)为:(1-2-10-3-7-4)
观察可知:(LCA(x,y))一定出现在(c[s[x]-s[y]])中,且为深度最小的一个。
根据以上结论,我们就把找(LCA)转化成了找区间最小值。于是就可以愉快地上(ST)表了。
与之前略有不同的是,我们还需要另外存一下取到的最小点的编号。
代码实现
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 10;
int n,m,S,head[maxn],num;
int st[maxn][30],p[maxn][30],s[maxn * 2],c[maxn * 2],top,dep[maxn]; //p为最小点的编号
struct Edge{
int then,to;
}e[maxn * 2];
void add(int u, int v){e[++num] = (Edge){head[u], v}; head[u] = num;}
void DFS(int x, int f, int deep){
dep[x] = deep;
c[++top] = x; s[x] = top;
for(int i = head[x]; i; i = e[i].then){
int v = e[i].to;
if(v != f){
DFS(v, x, deep + 1);
c[++top] = x;
}
}
}
int LCA(int x, int y){
x = s[x], y = s[y];
if(x > y) swap(x, y);
int k = (int)(log(y - x + 1) / (log(2)));
if(st[x][k] < st[y - (1 << k) + 1][k]) return p[x][k];
return p[y - (1 << k) + 1][k];
}
int main(){
scanf("%d%d%d", &n, &m, &S);
for(int i = 1; i < n; ++ i){
int u,v; scanf("%d%d", &u, &v);
add(u, v); add(v, u);
} DFS(S, 0, 1);
int N = 2 * n - 1;
for(int i = 1; i <= N; ++ i) st[i][0] = dep[c[i]], p[i][0] = c[i];
for(int j = 1; (1 << j) <= N; ++ j)
for(int i = 1; i + (1 << j - 1) <= N; ++ i)
if(st[i][j - 1] > st[i + (1 << j - 1)][j - 1]){
st[i][j] = st[i + (1 << j - 1)][j - 1];
p[i][j] = p[i + (1 << j - 1)][j - 1];
}
else{
st[i][j] = st[i][j - 1];
p[i][j] = p[i][j - 1];
}
while(m --){
int x,y; scanf("%d%d", &x, &y);
printf("%d
", LCA(x, y));
}
return 0;
}
单次查询时间复杂度(O(1)).