软件工程个人项目作业
| 项目 | 内容 |
|---|---|
| 这个作业属于哪个课程 | 班级博客 |
| 这个作业的要求在哪里 | 作业要求 |
| 我在这个课程的目标是 | 系统地提升软件工程能力 |
| 这个作业在哪个具体方面帮助我实现目标 | 掌握个人软件开发流程 |
| 教学班级 | 006 |
| Github项目地址 | https://github.com/Eadral/SE_Individual_Project |
PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 30 | 20 |
| · Design Spec | · 生成设计文档 | 5 | 15 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 5 | 5 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 10 |
| · Design | · 具体设计 | 10 | 10 |
| · Coding | · 具体编码 | 120 | 150 |
| · Code Review | · 代码复审 | 20 | 10 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 60 | 240 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 30 | 30 |
| · Size Measurement | · 计算工作量 | 10 | 10 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 60 | 90 |
| 合计 | 370 | 600 |
解题思路
求交点
首先考虑最基本的问题,如何求交点。
理想的情况是在数学上推导出一个完整的公式,尽可能减少中间步骤,减少耗时的以及可能带来精度损失的计算,同时有完整的判别公式用于判定点的数量,做到不重不漏。查阅资料后我主要参照Wolfram Mathworld [1] [2] [3],以及博客[4]完成的实现。
去重
题目要求输出点的数目,如果能求出任意两个几何对象的交点的话,那么只要能够去除重复的点即可得到答案。
去重有两种实现方案:
- Set(Hash table):每当求出一个交点,就将其插入set中,最终输出set中元素的个数即可。
- 排序:每当求出一个交点,将其插入数组尾部,最后对数组进行排序去重,不同元素的个数即是答案。
从理论上看,第一个方案时间复杂度为(O(m)),第二个方案时间复杂度为(O(mlogm)) ((m)为交点个数, 规模为(O(n^2)), (n)为几何图形个数),但是在现代计算机上实际运行时,缓存是一个影响很大的因素,如果没有经过特定优化,hash table的访存连续性较差,缓存命中率不高,而快速排序能够很好的利用缓存,性能非常好。现代计算机的CPU运算速度很快,计算应用几乎总是memory-bound。而且题目中限制了交点数量不会超过5百万个,排序5百万个点不会超过1s。这里我选择了第二种方案。
设计实现
类设计
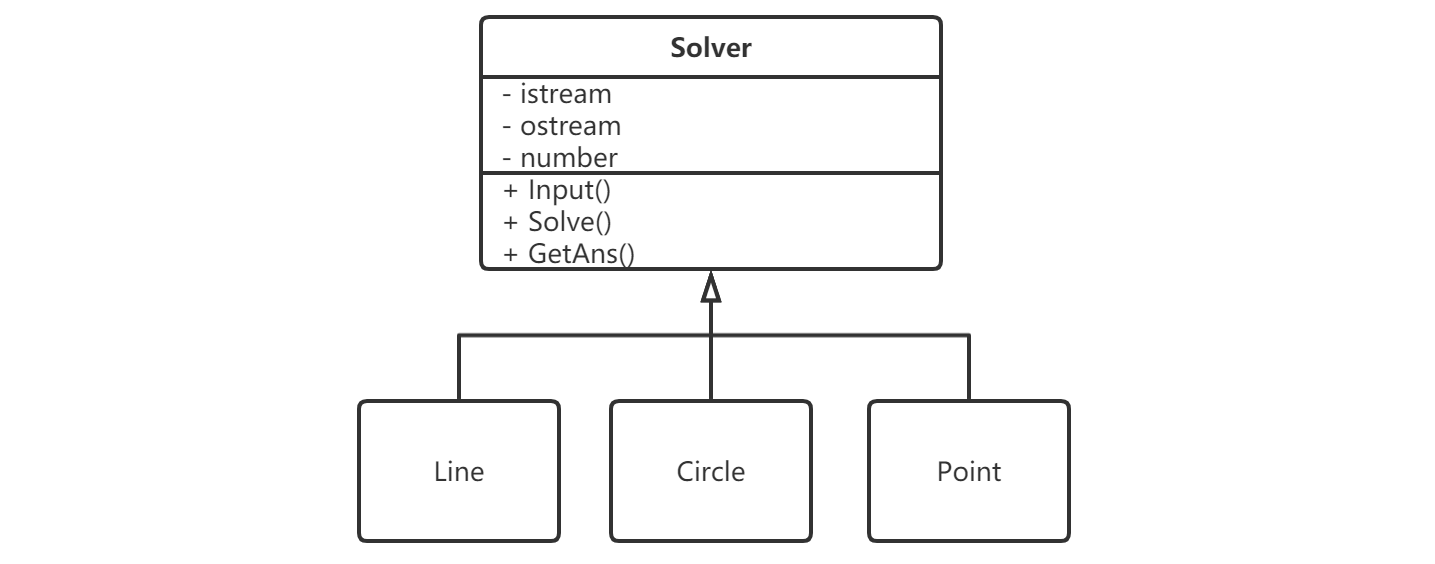
考虑编写面向对象程序。这个题目涉及的类有Line,Circle,Point,为了解题应当还有一个Solver。
其中Line,Circle,Point都是不变对象,可以选择使用struct实现,其中Point涉及比较,因此会重载比较运算符,并且在这里需要进行精度判断。因为参数的规模是(10^5),曲线最高是二次,因此需要(10^{10})的精度,double类型可以满足要求。
Solver需要获取以上类的对象信息进行求解,这里我选择Solver去组合Line,Circle,和Point。Solver还需要进行IO操作,可以设计成构造时获取IO流,并提供Input和Output接口。
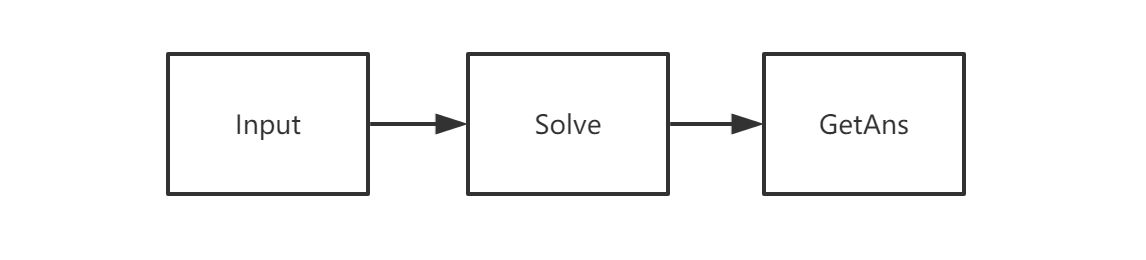
Solve流程
-
从流中获取输入,构建Line和Circle数组。
-
求交点:遍历Line,Circle数据,两两求交点。交点插入到Point数组中。
- Line-Line
- Line-Circle
- Circle-Circle
-
对Point数组进行排序去重。
-
将答案输出到流。
单元测试设计
单元测试应当存在多个粒度,本题没有很复杂的类间关系,其中Line,Circle作为没有方法的不变类,没有必要进行单独的测试。Point只涉及比较,可以在去重排序中完成覆盖。因此单元测试分为以下几类。
1. 交点测试:测试Solver的Line-Line,Line-Circle,Circle-Circle求交点方法分别测试,断言交点数量。
2. 错误测试:对错误输入,异常情况进行测试,断言输出的错误类型。
3. End-to-End测试:向Solver提供输入字符流,对输出字符流进行断言。
性能改进
排序去重
一开始选择的是排序去重方案。随机测试后发现,几何图像数量超过1万后十分缓慢,因为中间过程中交点个数太多了,vector会占据大量的内存,甚至导致程序崩溃。
Hash table
Hash table则不会造成产生大量中间点,改成unordered_set后,虽然不会在中间过程中产生过多的点了,但是hash的计算十分缓慢。而且hash造成的缓存不命中很可能显著影响效率。
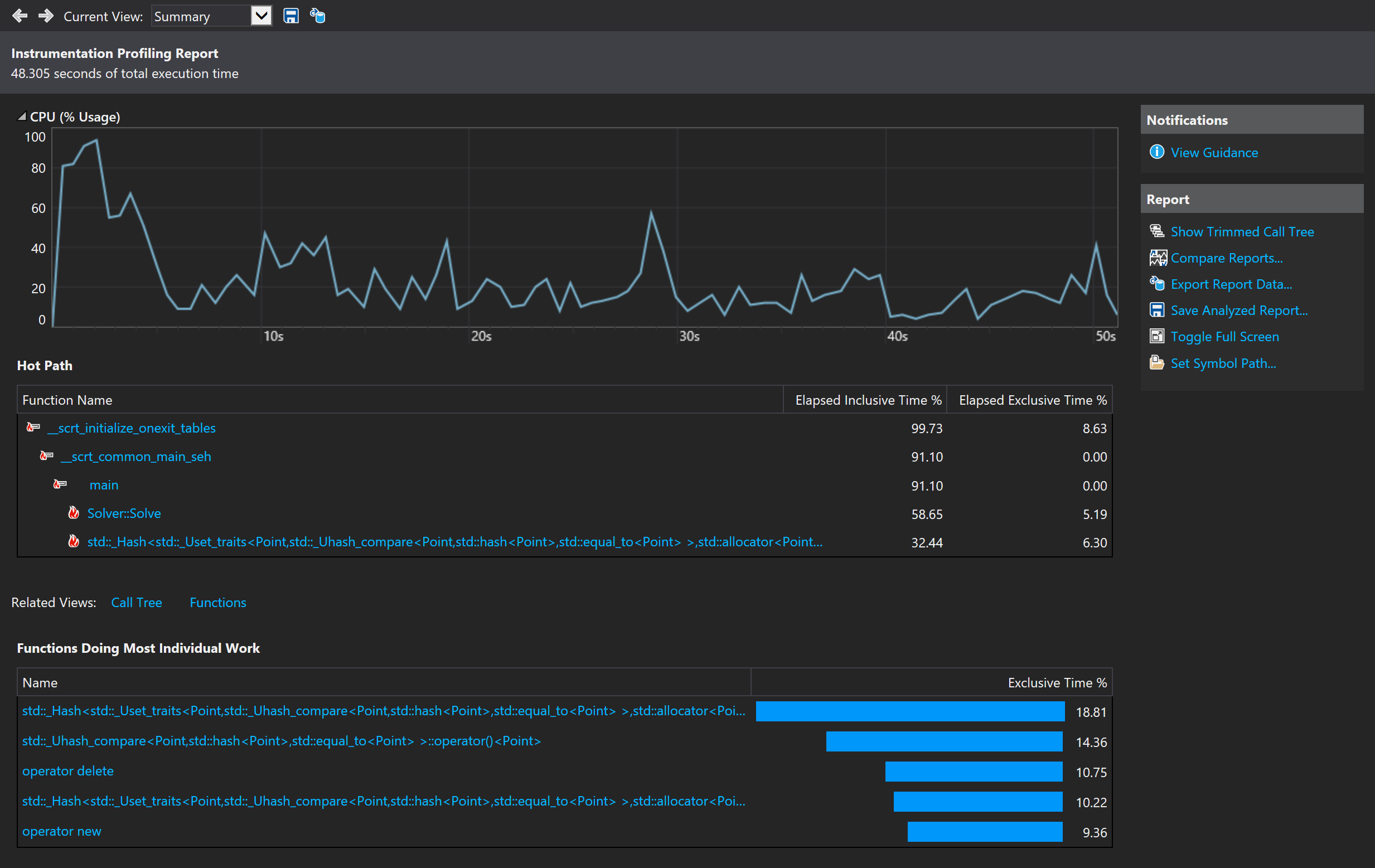
Hash 性能较差
排序去重改进
最终我选择了"定期"去重的方法,如果点的数量超过一个指定个数,则进行去重,这样就不会积攒太多的中间点,同时有效利用排序的高效性。
使用大量平行线进行测试后发现,求线交点的运算是性能瓶颈,因此考虑对这一部分进行优化。
Profiling热点
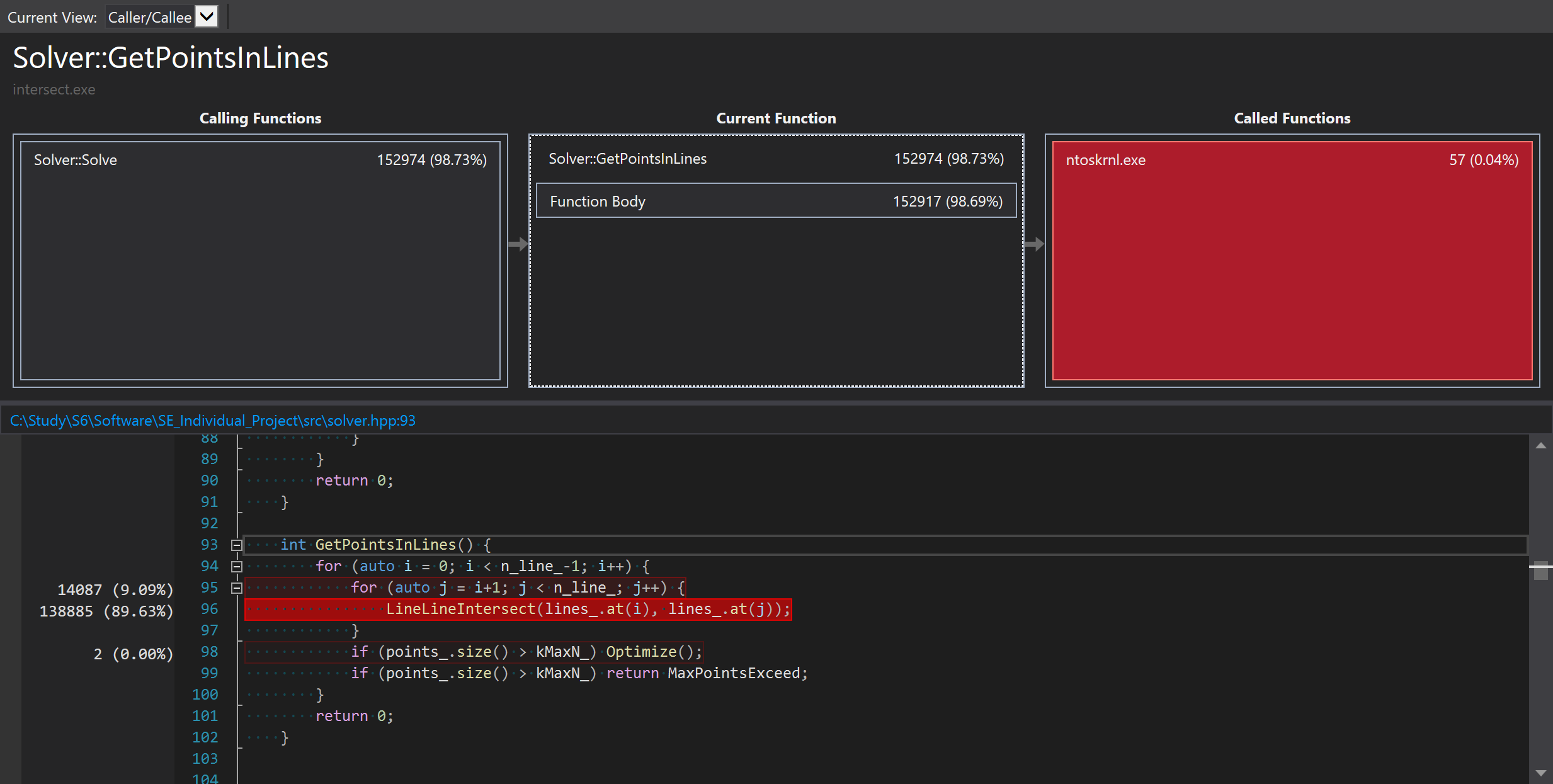
通过将关于单点的运算移动至Line的构造函数中,可以减少求交点时的重复计算,能够一定程度上提升性能。
struct Line {
long long x1, y1, x2, y2;
long long dx, dy, x2y1, x1y2, x2y1_x1y2;
Line(const int x1, const int y1, const int x2, const int y2) noexcept
: x1(x1), y1(y1), x2(x2), y2(y2)
{
dx = (long long)x1 - (long long)x2;
dy = (long long)y1 - (long long)y2;
x2y1 = (long long)x2 * (long long)y1;
x1y2 = (long long)x1 * (long long)y2;
x2y1_x1y2 = x2y1 - x1y2;
}
};
中等规模平行线,和小规模随机数据下,有着较好的性能。
1000000交点随机数据性能
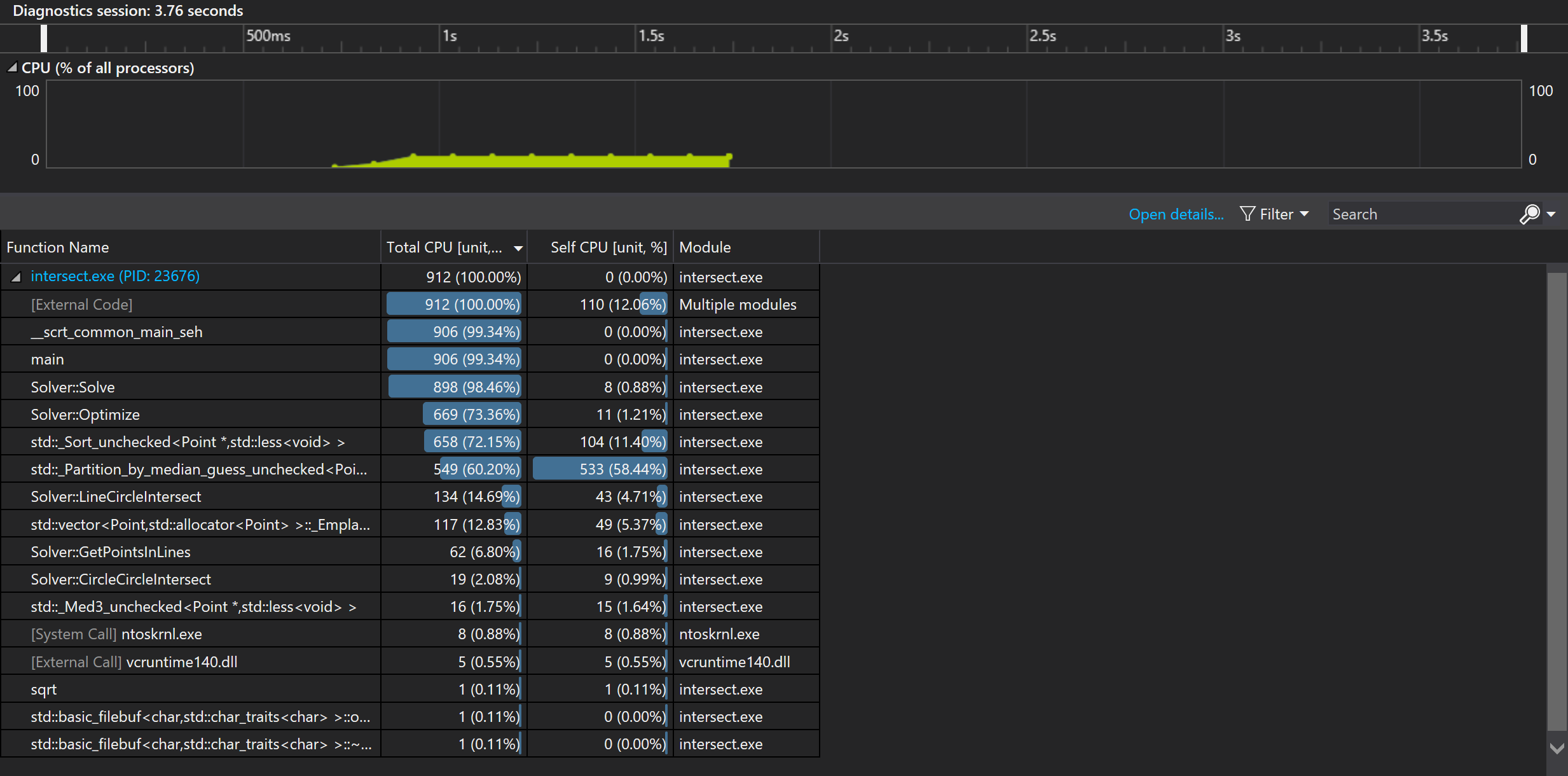
代码说明
数据结构
Circle,Line,Point以不变类为基础,进行了一些优化,并且Point重载了一些运算符。
struct Circle {
int x, y, r;
Circle(const int x, const int y, const int r) noexcept : x(x), y(y), r(r) {}
};
struct Line {
long long x1, y1, x2, y2;
long long dx, dy, x2y1, x1y2, x2y1_x1y2;
Line(const int x1, const int y1, const int x2, const int y2) noexcept
: x1(x1), y1(y1), x2(x2), y2(y2)
{ /* ... */ } // 预计算dx,dy等数值
};
struct Point {
double x, y;
Point(const double x, const double y) noexcept : x(x), y(y) {}
friend bool operator==(const Point& lhs, const Point& rhs) noexcept {
return abs(lhs.x - rhs.x) <= kEps && abs(lhs.y - rhs.y) <= kEps;
}
// ... < 运算符重载
};
求解
Solver对以上对象进行组合,并且持有流的引用以进行IO操作。
class Solver {
istream &in_;
ostream &out_;
vector<Line> lines_;
vector<Circle> circles_;
vector<Point> points_;
// ...
public:
Solver(/* ... */) {//...} // 初始化
int Solve(); // 求解,返回值为错误码
int GetAns(); // 返回答案
private:
int Input(); // 获取输入,返回值为错误码
void LineLineIntersect(const Line& a, const Line& b);
// ......
Solver主要提供Solve,GetAns方法,完成计算和结果的获取。其中Solve进行交点计算,并带有错误处理。
int Solve() {
auto err = Input();
if (err) return err;
err = GetPointsInLines();
if (err) return err;
err = GetPointsInCircles();
if (err) return err;
err = GetPointsBetweenLinesAndCircles();
if (err) return err;
out_ << GetAns() << endl;
return 0;
}
实际的计算则是for循环进行两两求交点。
int GetPointsInLines() {
for (auto i = 0; i < n_line_-1; i++) {
for (auto j = i+1; j < n_line_; j++) {
LineLineIntersect(lines_.at(i), lines_.at(j));
}
// ...
}
return 0;
}
交点计算则是套用数学公式,但是要考虑精度问题,[-kEps, kEps]之间的数被视作0。
void LineLineIntersect(const Line& a, const Line& b) {
const auto denominator = a.dx * b.dy - b.dx * a.dy;
if (denominator == 0)
return;
const auto x_numerator =
a.x1 * (a.y2 * b.dx + b.x2y1_x1y2) + a.x2 * (a.y1 * -b.dx - b.x2y1_x1y2);
const auto y_numerator = (b.dy) * (-a.x2y1_x1y2) + (a.dy) *(b.x2y1_x1y2);
auto x = (double)x_numerator / denominator;
auto y = (double)y_numerator / denominator;
points_.emplace_back(x, y);
}
最后通过排序去重得到答案
sort(points_.begin(), points_.end());
const auto new_end = unique(points_.begin(), points_.end());
points_.erase(new_end, points_.end()); // points_.size()即是答案
单元测试
通过18个单元测试完成了100%覆盖。
Code Coverage Results

通过所有单元测试
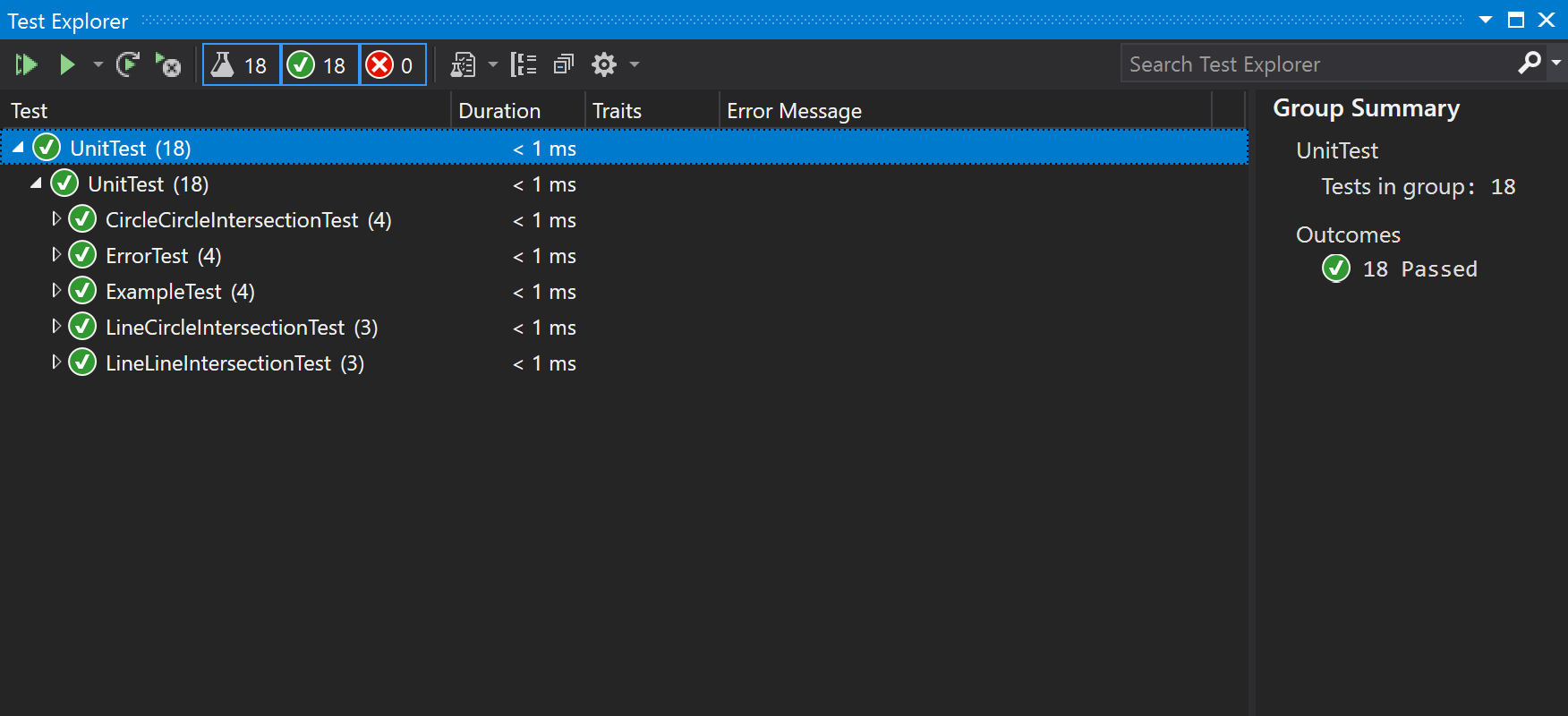
代码检查
通过 Code Quality Analysis 的检查,没有警告。
总结
填写PSP可以帮助我进行一些反思,这次项目的测试时间明显超支了,因为一开始把精度问题想的比较简单,到测试阶段才发现问题,花了比较多的时间去验证和修改代码,对整体进度影响比较大,之后应该强制自己再多花一点问题在前期的分析上。这次问题的复杂度比较低,之后面对结对项目,团队项目或者更大的项目应该更加谨慎,多做总结和分析。
通过这次作业,我也开始更加严格的要求自己遵守软件工程规范,例如不再随意提交commit,而是认真写标题和内容并做好分类,期间查阅资料也学到了不少,希望之后在这门课上取得更大收获。
参考资料
[1] https://mathworld.wolfram.com/Circle-CircleIntersection.html
[2] https://mathworld.wolfram.com/Line-LineIntersection.html
[3] https://mathworld.wolfram.com/Circle-LineIntersection.html
[4] https://blog.csdn.net/qq_18509807/article/details/84950132