跳台阶

时间限制：C/C++ 1秒，其他语言2秒 空间限制：C/C++ 32M，其他语言64M

题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

 

思路：设置一个函数F(N)表示走到第N级台阶走法的数量，现在假设有10级台阶，有两种情况：

　　1、从第9级，跨1级上来，到10级

　　2、从第8级，跨2级上来，到10级

　　对任何第N级台阶，都会出现两种情况，即第N级的前一步是走了1级或者是2级

　　如果统计10级的话，会有F(10) = F(9) + F(8)，即走到底10级的走法等于走到第9级的走法+走到第8级的走法，以此类推，F(9) = F(8) + F(7),F(8) = F(7) +F(6).....最后F(3)= F(2)+F(1)，F(2) = 2,F(1) = 1。

　　因此我们就可以得到动态规划中所谓的状态转移方程：F(N) = F(N-1)+F(N-2)

　　此时，我们可以中递归的方法解决这个问题：

class Solution {
public:
    int jumpFloor(int number) {
        if(number < 1)
            return 0;
        if(number == 1)
            return 1;
        if(number == 2)
            return 2;
        return jumpFloor(number -1 ) + jumpFloor(number - 2);
    }
};

　　使用递归时间复杂度较高

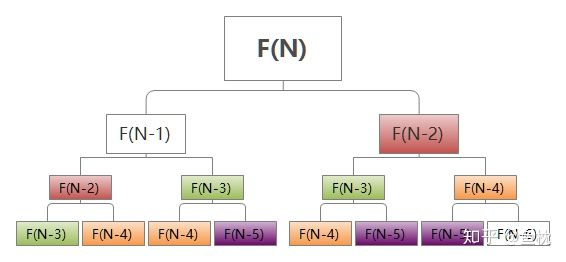
 　　递归的过程中可以构造一棵二叉树，时间复杂度会达到O(2^N).

　　使用动态规划的方法，自底向上求解问题，刚才递归是从顶往下构造了一棵树，现在才去自底向上构造，F(1)=1和F(2)=2,所以我们可以知道F(3) = F(2) + F(1) = 3,进一步地，我们可以知道F(4) = F(3) + F(2) = 5,等等等等…

　　此时时间复杂度就是O(N)

class Solution {
public:
    int jumpFloor(int number) {
        if(number == 1)
            return 1;
        int *step = new int[number + 1]();
        step[1] = 1;
        step[2] = 2;
        for(int i = 3;i <= number ;i++)
        {
            step[i] = step[i - 1] + step[i - 2];
        }
        return step[number];
    }
};

　　在C++11中的数组初始化中，定义了int *step = new int[10],只是为其分配了空间，并返回该数组第一个元素的地址给step指针，并未初始化，因此需要使用()进行初始化操作。否则程序不执行初始化操作 

int *step = new int[10]; // 每个元素都没有初始化
 
int *step = new int[10] ();  // 每个元素初始化为0

　　C++11标准中引进了新的初始化方式：用元素初始化器的花括号列表：

int *p = new int[10]{0,1,2,3,4,5,6,7,8,9};
string *p2 = new string[10]{"a","an","the",string(3,'x')};

　　注意虽然int[] a 数组名a本质上是指针，但属于常量指针，并不能进行接收new操作

什么是动态规划？
    动态规划（Dynamic Programming）是求解决策过程最优化的数学方法
    其大致思路是将一个复杂的问题转换成一个分阶段逐步递推的过程，从简单的初始状态一步一步递推，最终得到复杂问题的最优解
    动态规划解决问题的过程分为两步：
    1、寻找状态转移方程
    2、利用状态转移方程自底向上求解问题
参考：https://zhuanlan.zhihu.com/p/49427827