时间限制:C/C++ 1秒,其他语言2秒 空间限制:C/C++ 32M,其他语言64M
题目描述
给定一个数组A[0,1,...,n-1],请构建一个数组B[0,1,...,n-1],其中B中的元素B[i]=A[0]A[1]...A[i-1]A[i+1]...A[n-1]。不能使用除法。(注意:规定B[0] = A[1] * A[2] * ... * A[n-1],B[n-1] = A[0] * A[1] * ... * A[n-2];)
思路:
- 采用暴力方式求积
class Solution {
public:
vector<int> multiply(const vector<int>& A) {
int len = A.size();
vector<int> B;
if (A.empty())
return B;
int i = 0;
for (int i = 0; i < len; i++)
{
int multi = 1;
for (int j = 0; j< len; j++)
{
if (j != i)
{
multi *= A[j];
}
}
B.push_back(multi);
}
return B;
}
};
- 分别求出前i-1个元素的乘积,和后N-i个乘积分别保存在一个数组中,再将这两者相乘得到最终的结果(动态规划思想)
实例:
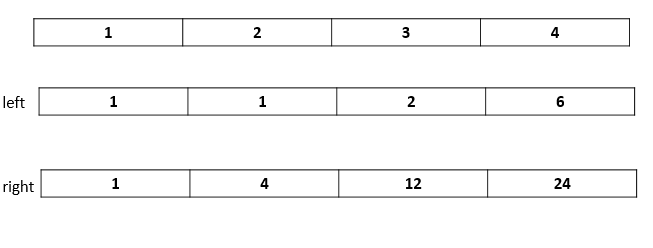
class Solution {
public:
vector<int> multiply(const vector<int>& A) {
int len = A.size();
vector<int> B;
int *left= new int[len];
int *right = new int[len];
left[0] =1;
right[0] = 1;
for(int i = 1;i < len;i++)
{
left[i] = A[i-1]*left[i-1];
right[i] = A[len-i] * right[i-1];
}
for(int i =0;i < len;i++)
{
B.push_back(left[i] * right[len-i-1]);
}
return B;
}
};
- 其实下面一种方法是对第二种方法的精简版本,思路是一样的,不过,这种方法并没有使用额外的空间求得最终结果。
class Solution {
public:
vector<int> multiply(const vector<int>& A) {
vector<int> vec;
int len = A.size();
if(len <= 0)
return vec;
vec.push_back(1);
for(int i =0;i < len-1;i++)
{
vec.push_back(vec[i]*A[i]);
}
int temp = 1;
for(int i = len-1;i>=0;i--)
{
vec[i] = vec[i]*temp;
temp = temp * A[i];
}
return vec;
}
};
解释下代码,设有数组大小为5。
对于第一个for循环
第一步:b[0] = 1;
第二步:b[1] = b[0] * a[0] = a[0]
第三步:b[2] = b[1] * a[1] = a[0] * a[1];
第四步:b[3] = b[2] * a[2] = a[0] * a[1] * a[2];
第五步:b[4] = b[3] * a[3] = a[0] * a[1] * a[2] * a[3];
然后对于第二个for循环
第一步
temp *= a[4] = a[4];
b[3] = b[3] * temp = a[0] * a[1] * a[2] * a[4];
第二步
temp *= a[3] = a[4] * a[3];
b[2] = b[2] * temp = a[0] * a[1] * a[4] * a[3];
第三步
temp *= a[2] = a[4] * a[3] * a[2];
b[1] = b[1] * temp = a[0] * a[4] * a[3] * a[2];
第四步
temp *= a[1] = a[4] * a[3] * a[2] * a[1];
b[0] = b[0] * temp = a[4] * a[3] * a[2] * a[1];
由此可以看出从b[4]到b[0]均已经得到正确计算。