时间限制:C/C++ 1秒,其他语言2秒 空间限制:C/C++ 64M,其他语言128M
题目描述
给你一根长度为n的绳子,请把绳子剪成整数长的m段(m、n都是整数,n>1并且m>1),每段绳子的长度记为k[0],k[1],...,k[m]。请问k[0]xk[1]x...xk[m]可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
输入描述:
输入一个数n,意义见题面。(2 <= n <= 60)
输出描述:
输出答案。
示例1
输入8
输出
18
思路:
动态规划
首先,我们知道如果一个长度为n的绳子可以分为 n = s[1] + s[2] + s[3] + s[4] 这么几个段,
那么一定有 max = s[1]s[2]s[3]s[4], 且 s[1] * s[2] 为长度是 s[1]+[s2]的子问题的最优解,同理s[3]s[4]一定是s[3]+s[4]的最优解,所以我们知道 n 其实可以表示为上述两段的最优解.
定义一个数组 max[0...61] 这里我们定义为长度为i(下标)的绳子能够构成的最优解长度,那么我们只要把这个定义成为一个二分问题,就是最优解的二分问题,(原理是:本问题的最优解一定是由子问题的最优解构成,如果你不能明白,那么请回过去看第一段话.)如果我们从最小的开始打表,那么试一下每两个问题的最优解,找到其中最大值就能得到本问题的解。
那么我们能够得到递推公式:
max[i] = Max(max[1]max[i-1],max[2]max[i-2], .... , max[i-1]max[1], i ) 当 i ≠ target时
max[i] = Max(max[1]max[i-1],max[2]max[i-2], .... , max[i-1]max[1]) 当 i = target时
这里你可能会有疑问,为什么我要包括 i 当不是目标解的时候, 也要试i,试这样的,我们继续看一下题干:
给你一根长度为n的绳子,请把绳子剪成整数长的m段(m、n都是整数,n>1并且m>1),每段绳子的长度记为k[0],k[1],...,k[m]。请问>>k[0]xk[1]x...xk[m]可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
-------- 发现绳子最少要切一刀,这个是一个比较烦的点, 首先举个例子。
f[长度] = 最少切一刀的最优解; 最少切一刀或者不切的最优解
f[1] = 1; 1 f[2] = 1, 2 f[3] = 2, 3 f[4] = 4, 4 f[5] = 6, 6 f[6] = Max( f[1]1[5],f[2]f[4] f[3] * [3]) = 9
这是我在计算f[6]时的过程,如果计算f[6],我们需要计算这些子问题的最优解
f[6] = Max( f[1]1[5],f[2]f[4] f[3] * [3]) = 9
那么可以看出来,我们对 6 做最优的二分已经保证了最少切1次,对于
f[6] = f[ x ] * f[6-x] 这两个子部分,最优解并不是必须切1次,可以不切.
f[6] = f[3] * f[3] 从结果上我们知道是3,那么就是3 * 3, 但是f[3] 如果二分结果并不是3 而是2最好的分法是不分, f[3] = 3, 这样你就理解了我为什么要加上 i 做最大值的比较,也理解了为什么不用i 做最终number的比较了吧。
class Solution {
public:
int cutRope(int number) {
int *dp = new int[61];
dp[1] = 1;
for(int i = 2;i < number;i++)
{
int maxs = i;
for(int j = 1;j<=i/2;j++)
{
maxs = max(maxs,dp[j]*dp[i-j]);
}
dp[i]= maxs;
}
int res = -1;
for(int i = 1;i<=number/2;i++)
res = max(res,dp[i]*dp[number-i]);
return res;
}
};
- 先举几个例子,可以看出规律来。
- 4 : 2*2
- 5 : 2*3
- 6 : 3*3
- 7 : 2*2*3 或者4*3
- 8 : 2*3*3
- 9 : 3*3*3
- 10:2*2*3*3 或者4*3*3
- 11:2*3*3*3
- 12:3*3*3*3
- 13:2*2*3*3*3 或者4*3*3*3
- 下面是分析:
- 首先判断k[0]到k[m]可能有哪些数字,实际上只可能是2或者3。
- 当然也可能有4,但是4=2*2,我们就简单些不考虑了。
- 5<23,6<33,比6更大的数字我们就更不用考虑了,肯定要继续分。
- 其次看2和3的数量,2的数量肯定小于3个,为什么呢?因为222<3*3,那么题目就简单了。
- 直接用n除以3,根据得到的余数判断是一个2还是两个2还是没有2就行了。
- 由于题目规定m>1,所以2只能是11,3只能是21,这两个特殊情况直接返回就行了。
- 乘方运算的复杂度为:O(log n),用动态规划来做会耗时比较多。
class Solution {
public:
int cutRope(int number) {
if(number ==2)
return 1;
if(number == 3)
return 2;
int x = number%3;
int y = number /3;
if(x == 0)
return pow(3,y);
else if(x == 1)
return 2 *2 *pow(3,y-1);
else
return 2 * pow(3,y);
}
};
链接:https://www.nowcoder.com/questionTerminal/57d85990ba5b440ab888fc72b0751bf8
为什么选择3的数学解释???
数学解释
问题类似于定周长求最大面积的问题(例如给定四边形周长,求最大面积),当k[0]k[1]...k[m]时乘积最大,设k[0]=x,那么n=x*m,乘积可以用下式表示
f(x)=(x)^(n/x)
下面是f(x)的导数:

乘积函数在n/m=e的时候,取得最大值,可知,当x∈(0,e)时f(x)单调递增,当x>e时,单调递减,因此,在x=e时取得最大值,e≈2.718,是自然对数。
从函数图像上也可以看出这一点
f(x)的函数图像
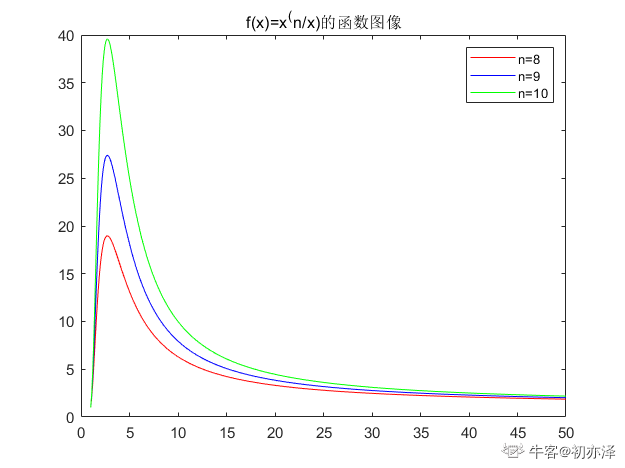
又因为x的取值只能为整数,且f(3)>f(2),所以,当n>3时,将n尽可能地分割为3的和时,乘积最大。 当n>3时,有三种情况,即n%30, n%31, n%32,如下所示

上式中除法向下取整
当n≤3时,只有
当n2时f(x)=1;
当n3时f(x)=2;
链接:https://www.nowcoder.com/questionTerminal/57d85990ba5b440ab888fc72b0751bf8