递归算法之汉诺塔

递归定义：

递归算法是把问题转化为规模缩小了的同类问题的子问题。然后 递归调用函数（或过程）来表示问题的解。

一个过程(或函数)直接或间接调用自己本身,这种过程(或函数)叫递归过程(或函数).

递归算法解决问题的特点：

(1) 递归就是在过程或函数里调用自身。

(2) 在使用递归策略时，必须有一个明确的递归结束条件，称为递归出口。

(3) 递归算法解题通常显得很简洁，但递归算法解题的运行效率较低。所以一般不提倡用递归算法设计程序。

(4) 在 递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储。递归次数过多容易造成 栈溢出等。所以一般不提倡用递归算法设计程序。

例子：汉诺塔

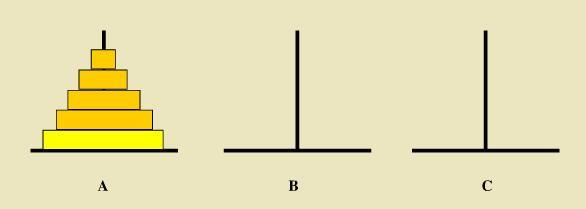
解：（1）n == 1

       　　　　　　第1次  1号盘  A---->C       sum = 1 次

       (2)  n == 2

       　　　　　　第1次  1号盘  A---->B

      　　　　　　 第2次  2号盘  A---->C

       　　　　　　第3次  1号盘  B---->C        sum = 3 次

　　（3）n == 3

　　　　　　　　第1次  1号盘  A---->C

　　　　　　　　第2次  2号盘  A---->B

　　　　　　　　第3次  1号盘  C---->B

　　　　　　　　第4次  3号盘  A---->C

　　　　　　　　第5次  1号盘  B---->A

　　　　　　　　第6次  2号盘  B---->C

　　　　　　　　第7次  1号盘  A---->C        sum = 7 次

不难发现规律：1个圆盘的次数 2的1次方减1

　　　　　　　2个圆盘的次数 2的2次方减1

                        3个圆盘的次数 2的3次方减1

                        。  。   。    。   。 

                        n个圆盘的次数 2的n次方减1

 故：移动次数为：2^n - 1

代码实现：

// topN盘子个数，from-->初始塔座 inter-->辅助塔座 to-->最终塔座
    public static void doTower(int topN, char from, char inter, char to) {
        if (topN == 1) {
            System.out.println("盘子1，从" + from + "塔座 到" + to + "塔座");
        } else {
            doTower(topN - 1, from, to, inter);
            System.out.println("盘子" + topN + "，从" + from + "塔座 到" + to + "塔座");
            doTower(topN - 1, inter, from, to);
        }
    }