不是完整的题解,乱记了一下,图片都是剽来的
CF504E Misha and LCP on Tree
二分+哈希。预处理 (2) 个哈希数组,一个从(root)到每个节点,一个从每个节点到(root)。注意处理转折的情况(即先从(a)到(lca),再从(lca)到(b)一段)
CF505E Mr. Kitayuta vs. Bamboos
二分答案,判断的时候把过程倒过来考虑。使用堆进行贪心
CF512D Fox And Travelling
环肯定选不了,拓扑把环都去掉,剩下的图构成森林。
对每棵树进行 dp 处理(背包),分为两类:有一个点和环连接或没有点和环连接
对于第一种情况,和环连接的点一定最后才能选,直接定为根进行书上背包,转移的时候乘上组合数
对于第二种,最后被选定的点无法确定,把每个点作为跟算一遍,然后去掉重复的
算完后再用背包合并计算最终
CF516D Drazil and Morning Exercise
首先(dist)很好计算,弄出一条直径,用两端分别更新答案即可。然后根据计算方法,发现如果以直径的中点为根,这棵树的(dist)值具有单调性(所有父亲节点的(dist)大于儿子)
有单调性后就可以双指针计算答案:先把所有点的(dist)扔到数组里排序,两个指针从末尾往前扫,其中一个(i)表示当前(dist)最小值,(j)表示最大值。由于最大的差值和(i)确定,不断把(j)移动,对于每个(i)更新答案。
把(j)移动相当于删除一个节点,而每个节点被删除时它的儿子节点一定已经被全部删除(单调性)。
用并查集维护子树的大小算出答案:初始时所有点的(fa)均为自己,每个(j)被删除后将其所在并查集(size - 1),每个(i)计算完后把它连接到其父亲节点所在的并查集
CF521D Shop
有三种类型的操作,观察后发现有以下性质
1、对于每个数如果要进行赋值操作,则一定在开头进行,且每个数最多赋值一次(最大的那个)
2、加法操作在乘法操作之前不会使答案更差
3、乘法操作放在最后进行,贪心选取大的进行操作
由第(3)条可以想到基本的做法:枚举乘法操作的个数
但赋值和加法放在一起不易处理,发现赋值其实可以看作是加法操作。假设第(x)个数当前为(now),加上的数为(v),可以算出对最后答案的贡献。按照贡献贪心选取。再与基本做法结合即可得到答案
注意在输出方案的时候要先输赋值操作
CF521E Cycling City
弄出一颗生成树,如果有边被覆盖(2)次及以上就存在答案
假设一条树边被连接了(x1,y1)和(x2,y2)的非树边覆盖,且这条树边的下端连接的是(x)
假设(x1)是(y1)的祖先,(x2)是(y2)的祖先,u=lca(y1,y2),v为(x1,x2)中深度小的那个
则存在三条从(u)到(v)路径:1、直接通过树上路径从从(u)到(v) 2、从(u)通过树边到(x1)再通过非树边到(x2)再通过树边到(v) 3、和(2)类似
直接用vector存储每条边被哪些非树边覆盖,对每条非树边暴力修改,因为如果大于一条就直接输答案了,复杂度有保证
CF526F Pudding Monsters
对于点((x,y)),对一个数组(a)进行(a[x]=y)的操作
由于每行每列只有一个,在选取的满足条件正方形中每行每列也只有一个
对应到序列(a)上就是一段长度为正方形边长(len)的连续子序列的(max-min+1=len)
用单调栈维护(min max),用线段树维护(max-min-len)的最小值和最小值个数,即在单调栈每次入栈出栈的过程中进行相应的修改,答案就是(=-1)的个数,而最小值一定为(-1)((len=1)时)
CF526G Spiders Evil Plan
对于每次询问,最后选取的路径是一颗包含(x)的子树,等同于以(x)为根,打通(2*y)个叶子节点到根的路径使得路径覆盖的总长度最大,因为选择叶子节点使得答案最优化,选取方式就是按照长链剖分处理出来的链长从大到小贪心选。然后这(2*y)条打通的从叶子到根路径一定可以拼成(y)条相交的路径
其实每次询问最后选取的子树不仅一定包含(x),还一定包含直径的至少一端。所以只要以两端为根分别预处理。对于询问(x,y),先贪心选取前(2*y-1)条长链,(-1)是因为直径的两端已经是一个叶子节点了。如果这样的方案已经包含(x)了就直接输出,否则有两种可能为最优解的更改方案
1、把最后一条选取的去掉,加上(x)所在的链 2、从(x)向上跳,把碰到的第一个已经选取的节点所在的链的下半部分替换为(x)所在的链 向上跳要预处理倍增
CF527E Data Center Drama
最终的图所有的点 入度+出度 一定为偶数,先考虑花最少的步数使其成立:在度数为奇数的点之间凉凉连边
最终的边数=总入度=总出度,也一定为偶数。如果加完后为奇数,随便找个点加上一个自环
如上处理后所加边数是必须的(最少的),其实这样已经存在一种方案了
处理前仍为无向图,且所有点度数为偶数,存在一条欧拉回路。把欧拉回路中的边的方向交替(正反正反)即为一组符合要求的答案。
因为在欧拉回路中,每个点被到达的次数和离开的次数一样。那么把方向交替,则每个点被经过一次要么 入读(+2),要么出度(+2),一定为偶数
CF536D Tavas in Kansas
最优解的方案不易找到规律,从结束状态向前dp处理。两个人的博弈游戏常用的方法:状态中设置一维表示当前轮到谁进行操作
观察到选取点的时候是把范围内的点全部选取,先预处理出(cnt(x,y))表示离第一个点距离不超过(x)且距离第二个点距离不超过(y)的点数,(sum(x,y))表示这些点的价值和。(f(x,y,p))表示当前剩余距离第一个点距离不超过(x)且距离第二个点不超过(y),轮到(p)选择的时候(p)获得的最大价值
转移只要枚举(p)选择覆盖的距离是多少即可,注意被覆盖的点数要 (>0)

记录一下部分的最小值来优化
CF538G Berserk Robot
横纵坐标相互影响不好处理,将坐标系逆时针旋转90°并将横纵坐标扩大(sqrt{2})倍
四个方向变成((1,1),(1,-1),(-1,1),(-1,-1))也就是说横坐标选什么和纵坐标选什么不影响
然后对一个循环的坐标更改量用不等式进行约束,并判断奇偶性,注意最后一段要单独处理
CF538H Summer Dichotomy
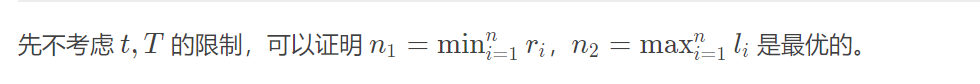
如果所有线段的交集不为空,那这样选可以选在这个交集内
否则如果有解,则把所有线段分成两部分后两个部分的线段交集不为空,此时 (n1) 为左边部分的最优位置, (n2) 为右边部分的左右位置,如果 (n1) 向右或 (n2) 向左就不符合要求了,然后如果 (n1+n2) 不在区间 ([t, T]) 内,如果多了,就减 (n1),少了加 (n2)
算出 (n1,n2) 后对于有些线段两个都符合,有些只能符合一个。将 (m) 对关系连边,先将只能符合一个的固定,向外拓展进行二分图染色判断是否可行。然后再对两个都符合且未被确定的线段随便指定 (1) 或 (2),进行同样操作
如果没有解,那随便怎么选都是 NO
CF547D Mike and Fish
对纵坐标相同的点随便配对两两连边,若有剩下的不管。对横坐标相同的点进行类似操作。进行二分图染色即为一种答案。
证明此时的图一定为二分图:
即:环中一条横边一定有一条竖边配对,长度一定为偶数。
CF547E Mike and Friends
先将所有字符串插入字典树,计算出 (fail) 指针,从所有的 (fail[i]) 向 (i) 连一条有向边,最后构成一颗“fail树”
对于字符串 (str) ,其在字典树中结尾的位置为 (w),则 (str) 在所有字符串中出现的次数即为“fail树”上以 (w) 为根的子树的贡献和
将所有询问离线差分,用 (vecotr) 存在每个位置,从 (1——n) 扫每个位置,处理到 (i) 时:
1、将第 i 个字符串的其所有前缀的贡献 +1,(在字典树上一直向上跳father)
2、处理在这个位置上的差分询问,加上贡献
子树的贡献和用dfs序+树状数组维护
CF555E Case of Computer Network
边双连通分量+树上差分
先用tarjan求出边双,缩点得到一棵树,随便定个根。然后处理每个条件,如果在同一个连通分量内则不用管,一定可以满足。否则以每个连通分量为节点进行差分:
用 2 中标记,一种标记表示边方向向下,一种向上,对于条件(x,y),把 x->lca 的路径向上标记,lca->y 的向下标记。最后统计如果有两种标记同时存在的边则输出“No”,否则“Yes”