7-1
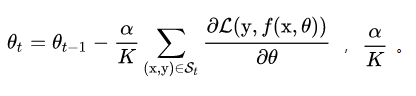
明显地,埃尔法和K成正比

7-2

7-3

7-4

7-5

7-6

7-7
从再参数化的角度来分析批量归一化中缩放和平移的意义
在此公式中,r和b表示缩放和平移参数向量。
- 通过r和b,能够有效适应不同的激活函数。例如:通过r和b,可以自动调整输入分布,防止ReLU死亡问题。
- 有了b的存在,仿射变换不再需要偏置参数。
- 逐层归一化可以提高效率,并且作为一种隐形的正则化方法,提高泛化能力。
7-8
批归一化可以应用于RNN的堆栈之间,其中归一化是“垂直”应用(即每个RNN的输出),
但是它不能“水平”应用(即在时间步之间),因为重复的rescaling会导致梯度爆炸。
主要是因为RNN梯度随时间反向计算,梯度有一个累积的过程。
7-9
证明在标准的随机梯度下降中,权重衰减正则化和l2正则化的效果相同。

分析这一结论在动量法和Adam算法中是否成立?
L2正则化梯度更新的方向取决于最近一段时间内梯度的加权平均值。
当与自适应梯度相结合时(动量法和Adam算法),
L2正则化导致导致具有较大历史参数 (和/或) 梯度振幅的权重被正则化的程度小于使用权值衰减时的情况。
7-10
当在循环神经网络上应用丢弃法,不能直接对每个时刻的隐状态进行随机丢弃,这样会损坏循环网络在时间维度上记忆能力。
(有点类似于7-8题,因为循环神经网络梯度计算是累加进行计算的,丢弃其中的某部分,会使得梯度计算不准确,即丢失记忆能力)
7-11

