记得一位大牛说过:计算机是人造学科,数学是神造学科。练过一段时间ACM,只记得比赛时只要和数学有关的题目都十分难搞。。。。
原来的博客中对知识点的总结比较零散,希望能在新博客中做一个系统的总结吧,但毕竟时间有限,想留出更多的时间去刷题(其实就是懒……),预计会大量引用自己csdn的博文和其他人的博客。
-
基本知识
(1)(x+y)%p=(x%p+y%p)%p;
(2)(x-y)%p=((x%p-y%p)%p+p)%p;
(3)x*y%p=((x%p)*(y%p))%p。
注意除法是不满足上述取模的规律的,除法取模需要用到乘法逆元,后面会讲到。取模次数过多会严重影响程序运行速度,具体题目具体分析,许多不必要的取模是可以省略的。
-
二分幂
二分幂又叫快速幂,算法的本名貌似是:蒙哥马利幂模。
它的主要功能是计 算 a^b%p( 模 p 可 有 可 无 ) 。
举个例子:不妨设 a=107,b=102,p=1000000007,如果我们求出了 x=a^51%p, 那么 x^2%p就是答案。那么下面就是求 a^51:我们求出了 x=a^25,那么 x^2*a就是答案。
更具体的描述参见:Hdu 4506 小明系列故事——师兄帮帮忙 +Hdu 1420 (蒙哥马利幂模算法)
和 二分求幂(pow的logn算法) - 枫轩缘 这里有图解、递归写法、非递归写法
//蒙哥马利幂模算法 //快速幂 //返回值(s^index)%mod __int64 Cal (__int64 s,__int64 index,__int64 mod) { __int64 ans=1; s%=mod; while (index>=1) { if ((index&1)==1) //奇数 ans=(ans*s)%mod; index>>=1; s=s*s%mod; } return ans; }上面这种写法还是比较完善的,目前没有被题卡过时间。目前做过的类型有:卡取模次数的(取多了TLE,取少了显然就爆__int64),卡先对底数取模的……
-
单个素数的判定:
从 2 到根号 n 枚举,判断是不是 n 的因子以判断 n 是不是素数。
-
筛法求素数
常用的方法大家都叫它“素数筛法”,其实它是有名字的:埃拉托斯特尼筛法
wiki对它有很详细的描述(英文的):Sieve of Eratosthenes
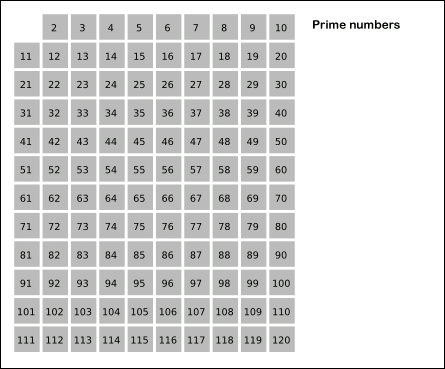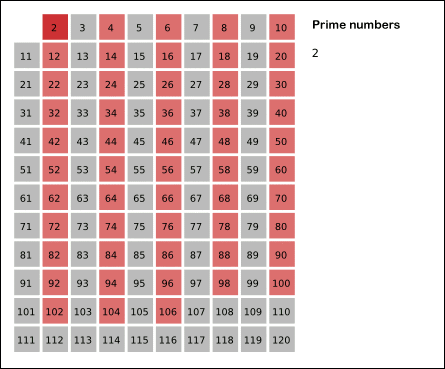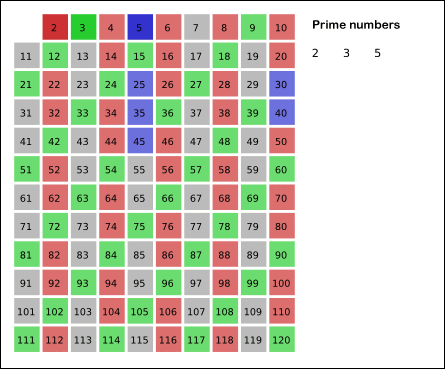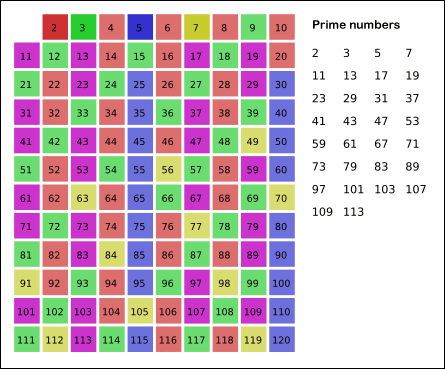
算法的基本思想是一个素数的除它本身外的所有倍数均为合数。下图(转自wiki)非常直观的描述了该素数筛法的基本原理:
具体实现:基本思想是首先标记所有数字为 0,然后从前向后找标记为 0 的,然后将该数的倍数(倍数大于等于 2)的数标记为 1。
const int NUM=1000004; int prime[79000],np=0; bool tag[NUM]; __int64 n; void Prime () //素数打表prime数组从0开始,范围内最大1000003 {//共np个素数,保存在prime[0]~prime[np-1] for (int i=2;i<NUM;i++) if (tag[i] == false) { prime[np++]=i; for (int j=i+i;j<NUM;j+=i) tag[j]=true; } }
一点补充:第二重循环可以改成 int j=i*i; 因为对于一个数x,假设它含有质因子i,那么令y=x/i;可以发现,如果x是小于i*i的数,那么其y值必小于i,在以前的筛选y的过程中,就会把x筛掉,所以没有必要重新筛选一遍。但是要注意两个int相乘有可能超范围……所以通常写作i+i,并没有慢太多。
-
约数个数
设 n=p1^e1*p2^e2*……pk^ek(pi均为素数,两两不等,ei为指数),则 n 的约数的个数为: (e1+1)*(e2+1)*……(ek+1)。这个用排列组合很容易证明。
例:12=2^2*3^1,那么 12的约数个数为(2+1)*(1+1)=6。
-
约数和
设 n=p1^e1*p2^e2*……pk^ek(pi均为素数,两两不等,ei为指数),则 n 的所有约数的和为:(p1^0+p1^1+ … … p1^e1)* … …(pk^0+pk^1……+pk^ek)。
例:12=2^2*3^1,那么 12 的约数和为:(2^0+2^1+2^2)*(3^0+3^1)=28。
给出数字 n,用 prime数组求出 n 的每个质因子以及质因子出现的个数
const int N=1; long long p[N],pNum[N],Num; void split (long long n) { Num=0;//np为素数个数,注意int相乘有可能会超int可表示的范围 for (int i=0;i<np && (long long)prime[i]*prime[i]<=n;i++) { if (n%prime[i]==0) { p[Num]=prime[i]; pNum[Num]=0; while(n%prime[i]==0) { pNum[Num]++; n/=prime[i]; } Num++; } } if (n>1) p[Num]=n,pNum[Num++]=1; }
-
欧拉函数
欧拉函数 phi(n)表示小于n 的正整数中与 n 互质的数的个数。比如 phi(1)=1,phi(2)=1,phi(3)=2,phi(4)=2。
- 单个数字欧拉函数的求法
设p1,p2……pk是n的k个质因数,f(n)=n*(1-1/p1)*……(1-1/pk)。
比如n=12,则p1=2,p2=3,那么f(12)=12*(1-1/2)*(1-1/3)=4。
int Euler (int n) { int i,ans=n; for (i=2;i*i<=n;i++) if(n%i==0) { ans=ans/i*(i-1); while (n%i==0) n/=i; } if (n>1) ans=ans/n*(n-1); return ans; }
- 欧拉函数的筛法
给出 N,求出 N 之内的每个数的欧拉函数。基本思想是枚举素数,判断该素数是哪些数字的质因子。
//求1到N的所有数的欧拉函数 const int N=5000005; i64 phi[N]; void init () { int i,j; phi[1]=1; for (i=2;i<N;i++) if (!phi[i]) for (j=i;j<N;j+=i) { if (!phi[j]) phi[j]=j; phi[j]=phi[j]/i*(i-1); } }
-
最大公约数
求两个数字 n 和 m 的最大公约数。欧几里得算法。
int Gcd (int x,int y) { return !y?x:Gcd(y,x%y); }
-
最小公倍数
Lcm(x,y)=x/Gcd(x,y)*y。
-
扩展欧几里得定理
给定两个数 a,b, 设 Gcd(a,b)=d, 则存在整数x,y,使得 x*a+y*b=d。
-
扩展欧几里得算法
就是上述方程中给定 a 和 b 求出 x,y。
我们知道,Gcd(a,b)=Gcd(b,a%b),而我们也就是运用这个东西来求a和b的最大公约数的 。因此,bx1+(a%b)y1=d, 由于 a%b=a-a/b*b,所以 bx1+(a-a/b*b)y1=d,所以:ay1+b*(x1-a/b*y1)=d。所以若 ax+by=d,那么显然 x=y1,y=x1-a/b*y1。注意,x,y可能是负值。
i64 Extended_Euclid (i64 a,i64 b,i64 &x,i64 &y) {//扩展欧几里得算法,求ax+by=gcd(a,b)的一组解(x,y),d=gcd(a,b) i64 d; if (b==0) { x=1;y=0; return a; } d=Extended_Euclid(b,a%b,y,x); y-=a/b*x; return d; }这个程序返回值为 Gcd(a,b),得到的 x 和 y 满足:ax+by=Gcd(a,b)。当然,如果给出的是求 ax+by=c(c不一定是 a 和 b 的最大公约数),这时当且仅当 Gcd(a,b)可以整除 c 时存在 x 和 y。 先求 ax+by=d 的一组解 x0,y0,设 k=c/d,x=x0*k,y=y0*k,则 x 和 y 就是一组解。通解为:X=x+t*b,Y=y-t*a。 (t 为任意整数)
-
乘法逆元
扩展欧几里得可以求乘法逆元。 乘法逆元的意思就是对于 a,p,若存在 b 使得 ab%p=1,则称 b 为 a 对 p 的乘法逆元。那么这个 b 有什么意思呢?对于一个数 x,x/a%p=x*b%p(a 可以整除 x) 。这样的话,就可以将除法变为乘法。那么怎么求 b 呢?ab%p=1,我们可得ab=kp+1(k 为某个整数),即 ab-kp=1,令 x=b,y=-k,则我们求出ax+py=1的一组解x,y即可。 这个式子有解的充要条件是Gcd(a,p)=1.
-
扩展阅读
#define i64 __int64 //求前n个数的约数个数和 i64 a[10]={0,1,3,5,8,10}; i64 f (i64 m) { if (m <=5) return a[m]; i64 sum = 0; i64 i; for (i = 1; i*i <= m; ++i) sum += m/i - (i - 1); return sum*2-i+1; } /* 数形结合,求在双曲线x*y = n在第一象限分支中下方的整点的个数。 作直线x=y,于是可以先计算上半部分(含x=y这条直线)的点数。 x=1的时候有m个,x=2的时候有m/2-1个。。。 于是乘以2。 然后x=y这条直线上的i-1个点多计算了一次,于是要减去(i-1)个。*/一些收藏的博文
当我真正理解了扩展欧几里得定理 - Accept - 博客园
【数论内容】线性筛素数,线性筛欧拉函数,求前N个数的约数个数 - M.J的blog - C++博客
【C/C++】位运算简介及实用技巧(二):进阶篇(1) - 八月照相馆的日志 - 网易博客