NormalMap是渲染过程中常见的一种贴图。它的作用是提供一张记录了模型法向分布的贴图。这样一来,可以用更少的面片数,获得更好的表现细节。下图展示了使用NormalMap的效果:

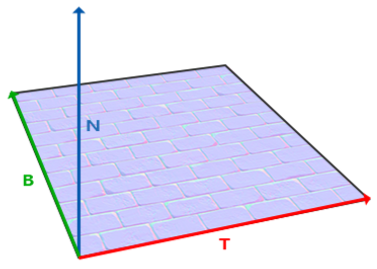
在实际读取具体顶点normal计算的时候会遇到一个问题:NormalMap中存储的法向信息是存储在Tangent空间里的。在这个空间中,将模型顶点向外的方向设置为向上的正方向(设该轴为N),除此之外还有两个轴Tangent和Bitangent(设为T和B),NBT三轴之前两两正交,如下图所示:
这样一来,我们需要一种将NormalMap中读取的normal从Tangent空间映射到模型局部坐标系的方法。这也是这篇文章讨论的重点。
考虑映射到NormalMap上的一个三角形,如下图所示,它的两条边的向量分别为E1、E2,对应纹理坐标的向量则为△U1、△V1,△U2、△V2,如下图所示:
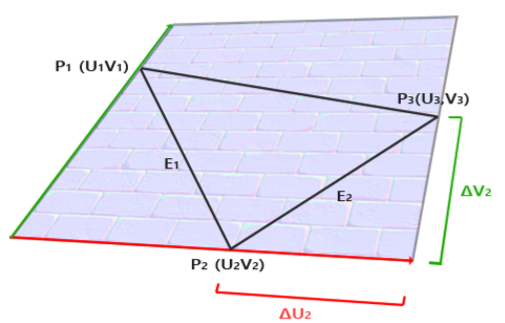
那么我们可以构建出以下的方程式:

该式可以转换成:

进一步列为矩阵的形式:

最终可以求解为:

这样一来就求解出了三角形的T和B。
根据以上的计算,我们可以通过如下流程,得到引入NormalMap的计算结果:
1.对模型的每一个三角形,利用如上的算法得到它们的T向量。
2.对模型的每一个顶点,将包含该顶点的三角形的T向量予以平均,得到顶点的T向量。
3.将顶点的T向量传入Shder中,在pixel shader里,利用向量的N和T之间的叉乘构建出Tangent空间的T、B、N三轴;有了这三轴以后,就可以构建出将normalMap里读取出的向量转化为世界坐标系的坐标。
4.最后将计算出的normal坐标参与光照计算,得到渲染结果。
值得一提的是,在shader中计算T、B、N三轴时,此时输入的是顶点的normal向量和tangent向量,他们之间未必是正交的。为了保证这一点,需要将tangent向量减去投影在normal向量中的部分,计算代码如下:
float3 T = normalize(tangent - dot(tangent, normal)*normal);
更直观的可以看下图来理解:
