低差异序列简介

在进行采样的过程中，经常需要生成随机数，为了能够得到一个尽可能好的采样结果，均匀的随机数是非常重要的。下图是我利用伪随机数采样得到的一系列点，可以看到其实还是不够均匀的：

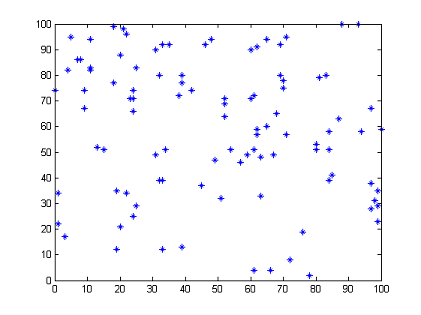
因此，如何得到一组分布均匀的随机数就成为了一个问题，本文所介绍的低差异序列技术就尝试解决它。
本文主要参考自：https://zhuanlan.zhihu.com/p/20197323 这篇文章

Radical Inversion

要介绍低差异序列，就要首先讲解一个基本的运算：Radical Inversion，它的定义如下：

其中i代表一个整数，b也是一个整数，(LARGE a_0(i))，(LARGE a_1(i))，(LARGE a_2(i))……(LARGE a_{M-1} (i))代表i在b进制下每一位的数，然后把每一位的a组成一个向量乘以一个矩阵C得到一个新的向量，再与向量(LARGE [b^{-1},b^{-2}...b^{-M}])相乘即得到i以b为底数，以C为生成矩阵的radical inversion (LARGE Phi_{b,C}(i))。
当C是单位矩阵的时候，我们就得到了Van der Corput序列：

下图展示了以2为底数的Van der Corput序列的例子：

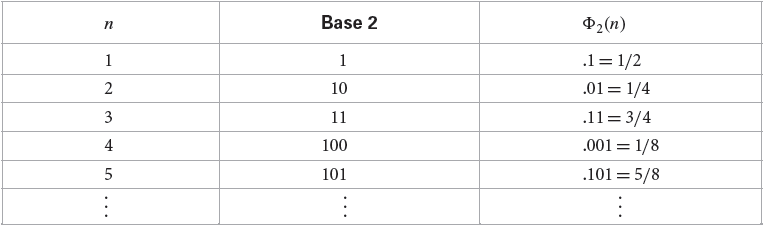
Van der Corput序列保证了每一个样本点会落在当前“最没有被其他点覆盖”的区域；此外，当样本个数达到(b^m)个点时，对[0,1)会形成均匀的划分。
很多时候Van der Corput序列并不能够代替伪随机数，因为点的位置和索引有很强的关系，例如在以2为底的Van der Corput序列中，索引为基数时候序列的值大于等于0.5，偶数时则小于0.5。

Halton序列与Hammersley点集

Halton和Hammersley基于Van der Corput序列，它们可以生成在无穷维度上分布均匀的点集。
Halton序列的定义如下：

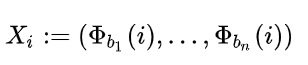
和Van der Corput序列的不同在于每一个维度的底数是不断变化的，其中(b_1,b_2,...,b_n)互为质数。
Hammersley点集的定义和Halton非常类似：

唯一的不同在于将第一个维度变成(LARGEfrac{i}{N})，其中i为样本点的索引，N为样本点集中点的个数。根据定义，Hammersley点集只能生成固定数目个样本，而Halton序列则可以生成无穷个样本。Hammersley的“差异度”比Halton更稍低一些，但是代价是必须预先知道点的数量，并且一旦固定没法更改。下图展示了Halton（左）和Hammersley（右）的二维采样示例：

下面展示了HLSL实现的Hammersly序列代码：

float VanDerCorpus(uint n, uint base)
{
	float invBase = 1.0 / float(base);
	float denom = 1.0;
	float result = 0.0;

	for (uint i = 0u; i < 32u; ++i)
	{
		if (n > 0u)
		{
			denom = fmod(float(n), 2.0);
			result += denom * invBase;
			invBase = invBase / 2.0;
			n = uint(float(n) / 2.0);
		}
	}

	return result;
}

float2 Hammersley(uint i, uint N)
{
	return float2(float(i) / float(N), VanDerCorpus(i, 2u));
}