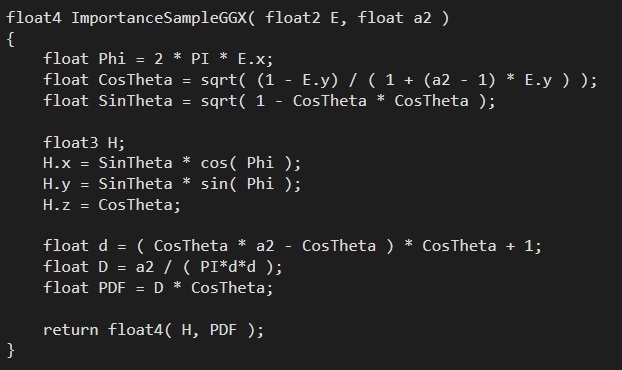
在之前的文章里面,我们介绍了Cook-Torrance BRDF,这是一种常见的用于表现PBR的光照模型。今天我们想要解决的问题是,在该BRDF下,给定物体材质的粗糙度(roughness),该如何生成符合该粗糙度的采样方向呢(这对于路径追踪采样生成入射光、IBL算法中采样计算radiance都很重要)?
法向分布函数(NDF)
对GGX的采样主要是针对它的法向分布函数NDF来进行的。在之前的文章中,我们曾经简单地介绍过法向分布函数的概念,它是一个用来描述微面元模型中各个微面的法向分布密度的函数。该函数实际的意义是当前点的微表面(microfacet)的面积除以宏表面(macrofacet)的面积,然后再除以立体角,所以NDF的单位是立体角分之一。
但是如果直接对NDF针对立体角dw积分的话,得到的结果其实并不是1,也就是说NDF实际上并不是法线的概率密度函数。
真正的归一化公式如下:
(LARGE int D(m)cos( heta_m)domega=1)
其中D是法向分布函数,m是某个微面元的法向,( heta_m)则是微面元的法向和宏观表面法向的夹角,(omega)是该微面元所属的立体角。这个公式其实就是将微面元的面积映射到了宏表面上,如下图所示:
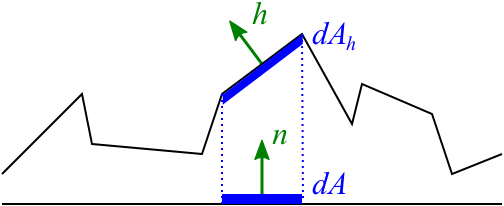
也就是说,如果上面的积分中没有这个(cos heta),那么得到的其实是微表面面积之和和宏表面之比。
更详细的理论推导可以参考这篇文章:How Is The NDF Really Defined?
通过上面的公式可知,(D(m)cos( heta_m))才是真正关于微表面法线的概率密度函数。
关于GGX的重要性采样
知道了概率密度函数p,我们就可以根据它进行采样。在这里我们以GGX的NDF为例。
GGX的NDF形式如下:
(large{NDF-GGX(n,h,alpha)=frac{{alpha}^2}{pi {( {cos heta}^2 ({alpha}^2 - 1) + 1)}^2}})
将它转换为球坐标系的概率密度函数为:
(large{p( heta,phi)=frac{{alpha}^2 cos heta sin heta}{pi {( {cos heta}^2 ({alpha}^2 - 1) + 1)}^2}})
求( heta)和(phi)的边缘概率密度函数,得:
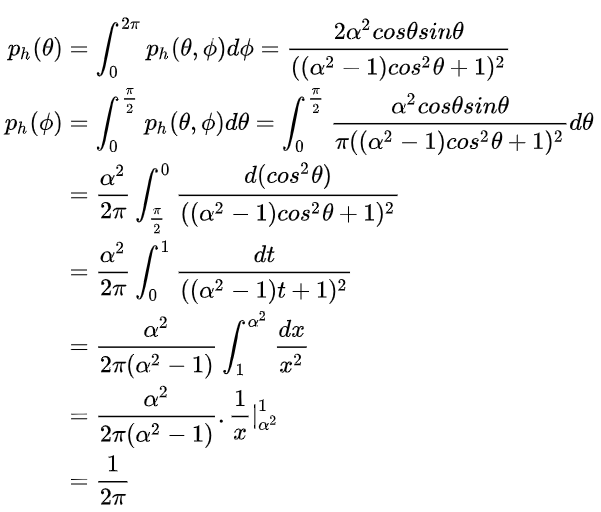
进一步求得( heta)和(phi)的CDF:
(LARGE P_h(phi)=frac{phi}{2pi})
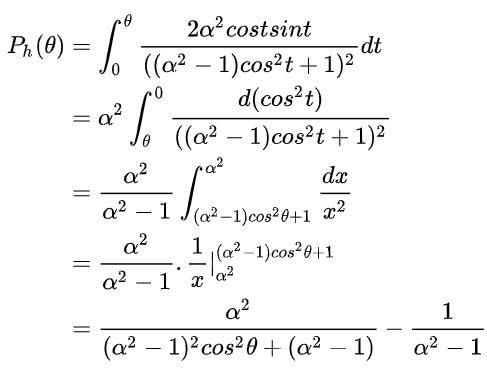
设两个[0,1]之间的随机数(xi)和(epsilon)分别对应(P_h(phi))和(P_h( heta)),可以解得(其实用得就是逆方法):
(LARGE phi = 2pixi)
(LARGE heta = arccossqrt{frac{1-epsilon}{epsilon(alpha^2 - 1) + 1}})
可以看到UE4中的GGX采样也是用该思路来计算的: