之前的文章里,我们介绍了实现IBL漫反射的方法。在这篇文章里我们更近一步,介绍基于镜面反射的IBL。
我们来看看我们要预计算的积分:
(LARGE L_o(p, omega_o)=int_Omega f_r(p,omega_i,omega_o)L_i(p,omega_i)n cdot omega_i domega_i)
并且
(LARGE f_r(p,omega_i,omega_o)=frac{DFG}{4(omega_ocdot n)(omega_i cdot n)})
这个积分涉及到了(omega_o),预计算所有方向的(omega_o)、法向(n)还有粗糙度r的组合将是一个天文数字,远远超出当前计算机的算力。
因此虚幻4引擎提出了一种近似计算的方法Split Sum,将这个积分拆分如下:
(LARGE L_o(p,omega_o)=int_Omega L_i(p,omega_i)domega_i ast int_Omega f_r(p, omega_i, omega_o)ncdot omega_i domega_i)
这个公式的前半部分可以看作是对环境光的预计算,后半部分则是一个和pbrf有关的值(对于同一个BRDF,该积分是相同的)。
预计算环境贴图
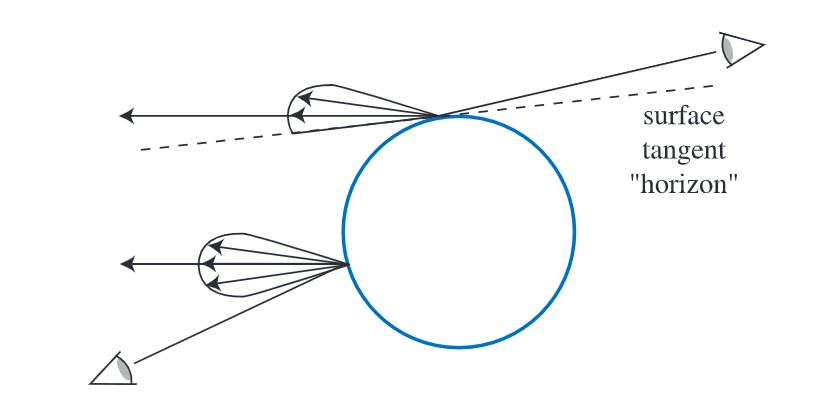
我们先来看第一个积分(LARGE int_Omega L_i(p,omega_i)domega_i),它计算的是环境光。这个积分需要针对法向分布函数进行重要性采样(参考之前的文章)。由于法向分布函数是针对h和n的分布函数,因为h=v+l,也就是需要知道出射方向V,即(omega_o),而我们预计算时是无法知道(omega_o)的。因此虚幻引擎又进一步做了一个假设,采用R=V=N时(即垂直观察表面时)的D的分布,这样就可以来计算这个积分了。当然,这么做实际上是和现实不一致的,因此与离线渲染的结果相比会有一定失真,如下图所示:
对这个积分采样时,需要将多个粗糙度不同的采样结果存储到一张贴图中,使用时再根据实际的粗糙度插值得出。
实际上,在虚幻四中,这个积分最终采用的离散计算公式如下:
(LARGE frac{sum_k^N L(omega_i^{(k)}) W(omega_i^{(k)})}{sum_k^N W(omega_i^{(k)})})
其中(LARGE W(omega_i) = n cdot omega_i)
所以也可以看到,为了实现实时的渲染,这个计算过程实际上很hack,很不物理。
然后我们来展示一下根据envMap预计算的代码:
float4 PS(VertexOut pin) : SV_Target
{
float t = (pin.Tex.x - 0.5) * PI * 2.0;
float p = (pin.Tex.y - 0.5) * PI;
float3 N = normalize(float3(cos(p) * cos(t), sin(p), cos(p) * sin(t)));
float3 R = N;
float3 V = R;
int SAMPLE_COUNT = 1024;
float totalWeight = 0.0;
float3 prefilteredColor = float3(0.0, 0.0, 0.0);
float2 tex_coord;
for (int i = 0; i < SAMPLE_COUNT; ++i)
{
float2 Xi = Hammersley(i, SAMPLE_COUNT);
float3 H = ImportanceSampleGGX(Xi, N, gRoughness);
float3 L = normalize(2.0 * dot(V, H) * H - V);
float NdotL = max(dot(N, L), 0.0);
if (NdotL > 0.0)
{
tex_coord = getSphericalMapTexCoordFromVec(L);
prefilteredColor += gEnvironmentMap.Sample(samLinear, tex_coord, 0.0f).rgb * NdotL;
totalWeight += NdotL;
}
}
prefilteredColor = prefilteredColor / totalWeight;
return float4(prefilteredColor, 1.0);
}
其中GGX重要性采样的代码如下:
float3 ImportanceSampleGGX(float2 Xi, float3 N, float roughness)
{
float a = roughness * roughness;
float phi = 2.0 * PI * Xi.x;
float cosTheta = sqrt((1.0 - Xi.y) / (1.0 + (a*a - 1.0) * Xi.y));
float sinTheta = sqrt(1.0 - cosTheta * cosTheta);
// from spherical coordinates to cartesian coordinates
float3 H;
H.x = cos(phi) * sinTheta;
H.y = sin(phi) * sinTheta;
H.z = cosTheta;
// from tangent-space vector to world-space sample vector
float3 up = abs(N.z) < 0.999 ? float3(0.0, 0.0, 1.0) : float3(1.0, 0.0, 0.0);
float3 tangent = normalize(cross(up, N));
float3 bitangent = normalize(cross(N, tangent));
return normalize(tangent * H.x + bitangent * H.y + N * H.z);
}
通过以上步骤,可以生成不同粗糙度的贴图,我们将它们作为一副图片的不同mipmap予以存储。
下图是LearnOpenGL官网给出的示例:

BRDF贴图
接下来我们来讨论第二个积分(LARGE int_Omega f_r(p, omega_i, omega_o)ncdot omega_i domega_i)
我们省略推导过程(想看推导的可以看看这篇文章),直接得出该积分推导后的结果:
(LARGE F_0 int_Omega f_r(p,omega_i,omega_o)(1-{(1-omega_o cdot h)}^5)n cdot omega_i domega_i + int_Omega f_r(p,omega_i,omega_o){(1-omega_o cdot h)}^5 n cdot omega_i domega_i)
(LARGE= F_0 scale + bias)
F0即是菲涅尔公式中的材质参数,因为我们采用的GGX是一个各项同性的BRDF(也就是(omega_o)和(n)的夹角( heta)才是决定渲染效果的值),所以实际上上式只需要两个变量就可以表示:(cos heta)和粗糙度(roughness),因此可以进行计算。计算出的贴图称作LUT,它的scale放在红色通道,bias放在绿色通道,我们所采用的BRDF的LUT如下:

最终的光照计算
有了这两张贴图,我们就可以结合diffuse和specular的irraidance来实现实时的IBL了。在这里展示一下最终计算ambient的shader代码:
float theta = atan2(pin.NormalW.z, pin.NormalW.x);
float phi = asin(pin.NormalW.y);
float3 ks = fresnelSchlickRoughness(max(dot(pin.NormalW, V), 0.0), F0, gMaterial.roughness);
float3 kd = (1.0 - ks) * (1.0 - gMaterial.metallic);
float3 irradiance = gIrradianceMap.Sample(samLinear, getSphericalMapTexCoord(phi, theta), 0.0f).rgb;
float3 diffuse = irradiance * gMaterial.albedo;
const float MAX_REFLECTION_LOD = 4.0;
float3 prefilteredColor = gPrefilterEnvMap.SampleLevel(samLinear, getSphericalMapTexCoordFromVec(R), MAX_REFLECTION_LOD * gMaterial.roughness).rgb;
float2 brdf = gBrdfLutMap.Sample(samLinear, float2(max(dot(pin.NormalW, V), 0.0), gMaterial.roughness), 0.0f).rg;
float3 specular = prefilteredColor * (ks * brdf.x + brdf.y);
float3 ambient = (kd * diffuse + specular)* ambient_weight;
渲染结果如下。可以看到,加入了specular的IBL镜面反射的效果非常明显:
