Grid Sorting

今天来看一道国外某高校算法课程的作业题，先看看题目描述：
In this part, you will implement SortGrid，which sorts the elements in a grid of integers.
Example:
Input:

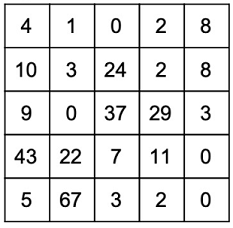
Output：

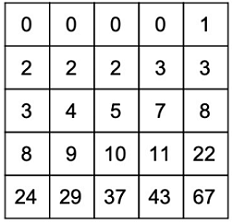
It is up to you to figure out a solution to this problem according to the requirements
below. We will test your solution for accuracy (i.e. does it sort the grid?) and for
efficiency. Points will be awarded based on accuracy and efficiency, so you should
design your solution with that in mind. Keep in mind that some algorithms may be
efficient on smaller grids or on specific grids but don’t work as well on other grids, so be
sure to test your solution on many different inputs.

Implementation Requirements：
You may use a two-dimensional array as a temporary copy in case you
decide to use a variation of MergeSort. You may not use that 2D array to
actually do the sorting in order to avoid getting more access counts.
e You may not copy the items over into a regular array of size N X N. In other
words, the sorting must be done in the grid.

这道题的题目描述意思大概就是对一个二维的数组进行排序，使之从左到右从上大小依次递增；同时，要保证是一个原地的算法，也就是空间复杂度为O（1）。
看到这道题，首先想到的就是将二维数组一维化，也就是将二维数组的坐标转化为一维坐标，假装对一个一维数组进行排序。
因为这道题要求必须是原地排序，像是MergeSort、QuickSort等方法都有一定的空间损耗，因此肯定就不能用它们了（更不用说QuickSort的最坏情况还是O（n^2））。这种情况可以考虑用堆排序来解决。
首先写一下二维转一维和一维转二维的代码，因为我们可以知道二维数组的大小，这个还是比较简单的：

#一维坐标转二维坐标
def convert_to_array_coordinate(data, index):
    N = len(data)
    x, y = int(index / N), index - int(index / N) * N
    return x, y

#一维坐标访问二维数组
def access_data_by_index(data, index):
    x, y = convert_to_array_coordinate(data, index)
    return data[x][y]

#一维坐标写二维数组
def write_data_by_index(data, index, val):
    x, y = convert_to_array_coordinate(data, index)
    data[x][y] = val

堆排序的代码如下所示：

def adjust_heap(data, index, length):
    child_index = index * 2 + 1    
    while child_index < length and index < length:
        child_val = access_data_by_index(data, child_index)
        if child_index + 1 < length and child_val < access_data_by_index(data, child_index + 1):
            child_index += 1
        child_val = access_data_by_index(data, child_index)
        cur_val = access_data_by_index(data, index)
        if child_val < cur_val:
            break
        write_data_by_index(data, index, child_val)
        write_data_by_index(data, child_index, cur_val)
        index = child_index
        child_index = index * 2 + 1
        

def merge_sort(data):
    N = len(data)
    if N == 1:
        return
    length = N * N
    # 构建大顶堆，时间复杂度为O（N）
    for i in xrange(int(length/2)-1, -1, -1):
        adjust_heap(data, i, length)
    
    # 每次获取堆顶元素，然后和堆底的元素交换（这样一来最大的数就到了“数组”最末），然后重新调整大顶堆，直至循环结束
    for i in xrange(length - 1):
        t = data[0][0]
        data[0][0] = access_data_by_index(data, length-i-1)
        write_data_by_index(data, length-i-1, t)
        adjust_heap(data, 0, length - i - 1)

当二维数组的大小为N×N时，我们可以认为是在对一个N×N长度的一维数组进行排序。

使用的时候代码如下：

data = [[4,1,0,2,8], [10,3,24,2,8], [9,0,37,29,3], [43,22,7,11,0], [5,67,3,2,0]]
merge_sort(data)

输出为：

[[0, 0, 0, 0, 1], [2, 2, 2, 3, 3], [3, 4, 5, 7, 8], [8, 9, 10, 11, 22], [24, 29, 37, 43, 67]]